
Figure 1. Finder chart for the 40 stars with secondary calibrations determined by Bruce Gary at the Hereford Arizona Observatory. FOV = 23.4 x 17.7 'arc; north up, east left.
This web page provides a list of B, V, g', r', i', z'
magnitudes for 40 stars in the open star cluster NGC 1342 in
Perseus. The magnitudes are based on two all-sky observations of
six Landolt star fields with primary standard stars for B- and
V-bands (Landolt, 2009) and g'r'i'z'-bands (Smith et al, 2002).
The coordinates for the center of this star field (Star#0) is
03:31:48 +37:20:36 (J2000). The "observing season" for this star
cluster is November 19 (when it crosses the meridian at local
midnight). My purpose for calibrating this star cluster is to
serve as a Fall counterpart to M67, which has a late winter
observing season (January 30). M67 has a long tradition of use for
establishing a telescope system's "transformation coefficients"
(star color sensitivity, mostly), but it has lacked a counterpart
for other seasons. I invite photometry observers to use the
magnitudes reported on this web page to complement M67 in
affording a greater seasonal coverage for establishing and
monitoring telescope system star color sensitivity coefficients.
(I've calibrated 47 stars in M67 for BVg'r'i'z' bands, and results
are given at link.)


Figure 1. Finder chart for the 40 stars with secondary
calibrations determined by Bruce Gary at the Hereford Arizona
Observatory. FOV = 23.4 x 17.7 'arc; north up, east left.
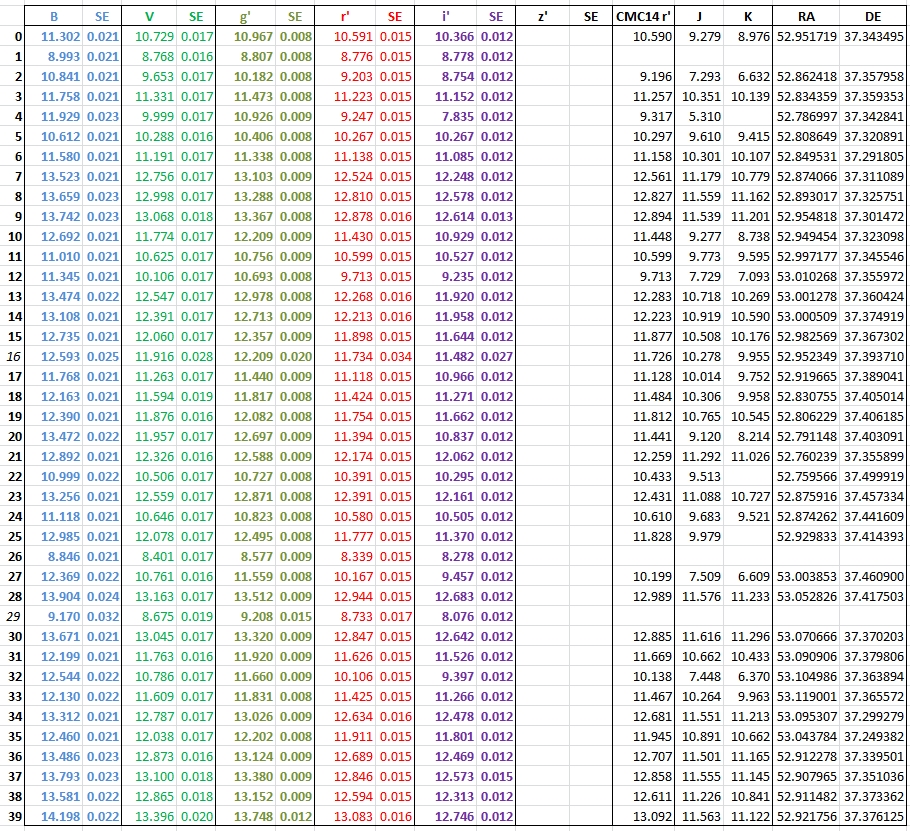
Figure 3. Magnitudes with estimated SE's.
Here's a downloadable text file of the above table: link.
Warning, magnitudes for stars 16 and 29 are slightly variable, so
don't use them for establishing zero shifts; their colors
are reliable so they can be used for evaluating "star color
sensitivity."
Rationale for Using an Open Star Cluster for Monitoring a
Telescope System's "Star Color Sensitivity"
My original plan for meeting all-sky photometry calibration needs
was to rely upon the AAVSO's APASS catalog. However, when I found
that the APASS magnitudes (DR5) for M67 had serious systematic
errors (on the order of 100 mmag), and when I realized that APASS
wouldn't include z'-band, I decided to perform the open star
cluster calibration described on this and my M67 web pages. My
intent was to have calibrated stars for my personal use, for ~ 3
open star clusters, but since a lot of work would be involved it
seemed appropriate to share my calibration results with web pages
for each star cluster.
I am fully aware of the need to be cautious in accepting someone
else's secondary star calibration results. I should therefore
state that any use of my M67 and NGC 1342 calibrated stars is done
with risk of being erroneous. I'm sure that Arne Henden would
discourage anyone from using my secondary standard stars for any
purpose. Please keep in mind that my secondary calibrations do not
have the benefit of peer review, and they are therefore
uncorroborated by any other observer. Keep in mind also that I am
an amateur, and anything amateurs do is treated with great
suspicion by professional astronomers. If I had a lawyer advising
me I'd have to state here that "Any material on this web page is
not meant for use for any purpose." You've been warned!
Estimating SE Uncertainties
Magnitude SE uncertainty was estimated by orthogonally adding
three components: 1) RMS of Landolt stars with respect to a fit,
2) RMS of NGC 1342 stars with respect to each other, and 3) the
difference between two all-sky observing sessions
(2012.11.26 and 2012.12.01). The first of these components has a
magnitude dependence, determined manually ("by eye") from the
Landolt stars. The second component was determined from 5
observing cycles made throughout the observing session (covering a
range of air masses). The last component was made using the
relationship that the average of two estimates with Gaussian
uncertainty is typically 1/2 of the difference between the two
values. For i'-band the difference was 1 mmag (between the two
observing dates), so the i'-band SE is essentially only due to the
first two SE components. For r'-band the two observing dates
differed by 12 mmag, so the final SE was dominated by the RMS
variation of Landolt stars with respect to the fits. For B- and
V-bands the differences were 27 and 23 mmag, so these were the
dominant SE component for B- and V-band.
The pattern for these observing session differences is
monotonically increasing in going from long to short wavelengths;
i.e., the differences increase with atmospheric extinction. This
suggests that the observing session differences are due to an
imperfect solution for atmospheric extinction, which are likely to
be proportional to total extinction for the band in question. This
is a reasonable interpretation, and it is supported by the
excellent agreement between the B-V star colors for both observing
sessions: the median difference between B-V star colors for the
two observing sessions is 2 mmag! In other words, B-V star colors
in the above table can be trusted more than the absolute
magnitudes. For g'-r' and r'-i' star colors, median differences
between the two observing sessions is 20 and 11 mmag. These star
color consistencies are gratifying since the principal objective
for this project is to calibrate an open star cluster for the
purpose of evaluating (e.g., monitoring) a telescope system's star
color sensitivity parameter.
The first SE component, RMS of Landolt stars, is attributed to
use of an imperfect "flat field" calibration. My master flat
fields were made using the sky at dusk, which has a blue color. In
theory, such a flat field should work better for blue stars than
red ones. Since I obtain flat fields using a blue illumination
source (instead of white) I should expect flat field calibration
errors that increase with wavelength (i.e., worst at the reddest
filter).
Comparison With Other Catalogs
The Carlsberg Meridian Catalog, Release 14 (CMC14), shows fainter
r'-band magnitudes than my all-sky values. The median difference
is 30 mmag, with a standard deviation about the average of 21
mmag. The CMC14 has an estimated SE < 25 mmag for stars with r'
< 13.
The rest of this web page is under construction ...
Information on the All-Sky Observing and Analysis
Procedures Used
My observing procedure is described elsewhere, http://brucegary.net/allsky2011/,
as is my hardware: http://www.brucegary.net/HAO/.
Briefly, I use a 14-inch Meade with a SBIG ST-10XME CCD. The
telescope is housed in a dome, and both are controlled from my
residence office using buried control cables. I use MaxIm DL for
control of the telescope, CCD, focuser and dome. Flat fields are
taken of the sky before sunset. Bias and dark exposures are also
taken before observations. All imaging is unbinned.
The April 16 all-sky observing session consisted of "observing
cycles" of Landolt star fields and M67. All exposure times are 10
seconds, unguided. An "observing cycle" consists of 4 B-band
images, 4 at V-band, 4 at g', 3 at r', 3 at i' and 5 at z'. Two
observing cycles are made whenever a Landolt star field is
acquired (some fields are acquired at different times of the night
for sampling a large range of air mass). On April 16 I observed
the following star fields: L0652, L0558, M67, L0724, L0853, M67,
L0853, L1637 (note that L0652 means the Landolt star field at RA =
06:52, DE ~ 0). After this sequence I observed L1637 for the rest
of the night for the purpose of detecting the presence of
sub-visible cirrus and aerosol patchiness (one events of ~15 mmag
lasting 1/2 hour was found, as was another with 5 - 10 mag). This
6-hour run also provided extinction trend information (that was
useful in constraining subsequent analyses involving extinction
change modeling).
The rationale for including B and V observations when only
g'r'i'z' magnitudes are to be determined has to do with the need
for an accurate star color for each star. There are many more B
and V standard magnitudes (Landolt 2009) than g'r'i'z' magnitudes
(Smith et al 2002) at each of the observed Landolt star fields.
I use an artificial star for all image analysis, which permits
monitoring of extinction variations. I have come to view the
presence of sub-visible cirrus and aerosol patchiness as very
important for all-sky observing, and the only way I know how to
deal with these extinction variations is with the use of an
artificial star (that occupies an unused 0.1% corner of each
image). The artificial star magnitude won't vary during an
observing session, so it allows star magnitude readings to be
converted to star flux.
All photometry readings correct for "flux capture fraction" - the
ratio of flux within the circular photometry circle when the
radius is small (~ 2.5 times FWHM) versus large (~5 times FWHM).
The small aperture is used for exporting to a spreadsheet for
subsequent analysis. The incentive for using a small photometry
aperture is twofold: bettyer SNR for faint Landolt stars, and
reduced interference from nearby stars. This correction is usually
20 or 30 mmag.
The spreadsheet calculates air mass from JD, my site location and
the target coordinates. All star fluxes are processed with
guidance from the following generic magnitude equation:
Magnitude = Z - 2.5 ×
LOG10 ( Flux / g ) - K' ×
AirMass + S × StarColor + S2
× AirMass × StarColor
(1)
where Z is a zero-shift constant,
specific to each telescope system and filter (which should remain
the same for many months),
Flux is the star's flux (sum of counts
associated with the star). It's called "Intensity" in MaxIm DL,
g is exposure time ("g" is an engineering term
meaning "gate time"),
K' is zenith extinction (units of
magnitude per air mass),
S is "star color sensitivity." S
is specific to each telescope system (and should remain the same
for many months),
StarColor can be defined using any two filter
bands. B-V is in common use; I use 0.57 × (B-V) -
0.39,
S2 is a second-order term that is
usually ignored because it is only important for high air mass and
extremely blue or red stars.
This general equation is true for all filter bands (even
unfiltered), though there are different values for the constants
for each filter. For example, the magnitude equation for V-band
(omitting the last term in Eqn 1) is:
V = Zv - 2.5 ×
LOG ( Flux / g ) - Kv' × AirMass + Sv ×
StarColor
(2)
Extinction at each filter band is represented by a zenith value
at mid-observing session time, a temporal trend parameter, and a
3rd order fit to residuals (identified as aerosol patches drifting
overhead).
Figure 4. Screen capture of a spreadsheet section for
V-band fitting of Landolt stars (N=54, total of 173 photometry
readings). Lower-left panel shows solution for zenith
extinction; upper-left panel shows solution for star color
sensitivity; upper-right panel shows residuals of measured
magnitude with respect to modeled magnitude versus V-magnitude.
Lower-right area ahs slide bars for matching RMS versus
magnitude (upper-right) with a stochastic SE model.
"Landolt Unknown" Analysis
A final adjustment was made by treating each Landolt star field
as an "unknown" and processing it using the other Landolt stars to
solve for telescope system photometry constants. Since five
Landolt star fields were used for the April 16 observing session
there were five estimates of "average star field error" for each
filter band. For example, the V-band average errors were +8, -2,
+8, -21 and +5 mmag. Some star fields had more standard stars than
others, and the average of the 54 Landolt stars in all star fields
for V-mag was +0 ± 11 mmag. For B, g', r', i' the average
errors were +3, +12, +9 and -4 mmag. z'-band was less well
behaved, with +49 mmag average error. Apparently there is
something about my analysis procedure for z'-band that was
underestimating star brightness when all Landolt star fields were
involved in the parameter solution. Until I figure this out I have
decided to adopt the correction values called for by the exercise
of treating Landolt star fields as unknown. This is what was done
in obtaining Fig. 2, above. The following table lists the "Landolt
Bias Corrections" for each band based on treating each of the
Landolt star fields as an "unknown."
Table 2. "Landolt Bias Correction" for Apr 16 (Based on
Treating Landolt Star Fields as Unknown)
| B |
V |
g' |
r' |
i' |
z' |
|
| Apr 16 Bias [mmag] |
+3 ± 12 |
+0 ± 11 |
+12 ± 7 |
+9 ± 4 |
-4 ± 4 |
+49 ± 25 |
| Apr 16 Nr. Comparisons |
54 |
54 |
16 |
16 |
16 |
16 |
| May 02 Bias [mmag] |
+9 ± 6 |
-1 ± 3 |
-5 ± 5 |
-2 ± 4 |
+2 ± 3 |
-11 ± 9 |
| May 02 Nr. Comparisons |
40 |
40 |
13 |
13 |
13 |
13 |
Total SE for each star will depend on the star's brightness,
since stochastic SE varies with star brightness and total SE is
the orthogonal sum of stochastic and estimated systematic SE. I
estimate that the systematic error for each band is the orthogonal
sum of the applied half of the "Landolt Bias Correction"
correction (above table) and the SE of that correction.
![]()
References
Henden, A. 2000, JAAVSO, 29, 35-43.
Landolt, A. U., 2009, AJ, 137, 4186-4269, May.
Smith, J. Allyn, et al, 2009, AJ, 123,
2121-2144.
Skiff, B., 1997, M67 catalog: http://stupendous.rit.edu/tass/catalogs/m67.html
RELATED WEB PAGE LINKS
AAVSO photometry manual: http://www.aavso.org/observing/programs/ccd/manual/4.shtml#2
Lou Cohen's 2003 tutorial: http://www.aavso.org/observing/programs/ccd/ccdcoeff.pdf
Priscilla Benson's (1990's) CCD transformation
equations tutorial: http://www.aavso.org/observing/programs/ccd/benson.pdf
Bruce Gary's CD Transformation Equations derived from basic
princples: http://reductionism.net.seanic.net/CCD_TE/cte.html
Bruce
Gary's All-Sky Photometry for Dummies: http://brucegary.net/dummies/x.htm
Bruce Gary's All-Sky
Photometry for Smarties - v1.0: http://brucegary.net/photometry/x.htm
Bruce Gary's All-Sky
Photometry for Smarties - v2.0: http://brucegary.net/ASX/x.htm
Bruce Gary's Differential Alternative
Equations: http://brucegary.net/DifferentialPhotometry/dp.htm
Bruce Gary's Astrophotos home page: http://reductionism.net.seanic.net/brucelgary/AstroPhotos/x.htm
Bruce Gary's all-sky observing session
of 2011.10.28 (BVRcIcg'r'i'z', 60 Landolt stars, 22 SDSS
stars): http://brucegary.net/yygem/all-sky/index.htm
Bruce Gary's 2011 version of all-sky observing
and analysis procedure: http://brucegary.net/allsky2011/
Bruce Gary resume: http://brucegary.net/resume.html
____________________________________________________________________
WebMaster: B. Gary. Nothing on this web page is copyrighted. This site opened: 2012.11.29. Last Update: 2013.02.19