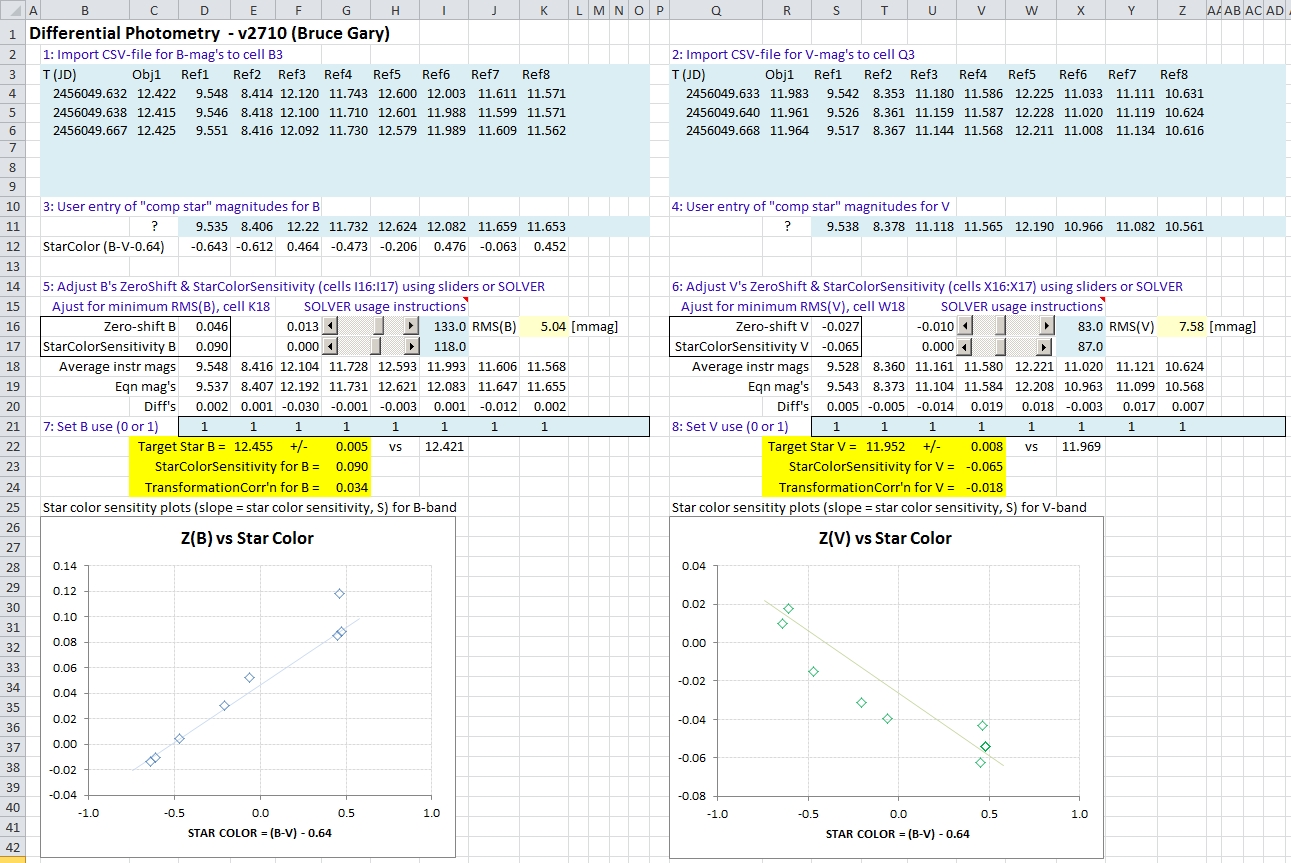
Excel spreadsheet DP2010.xlsx (2010 version of Excel), used for calculating "transformed" B & V magnitudes for a target star with nearby calibrated ("comp") stars.
Bruce L. Gary (GBL); Hereford, AZ, USA; 2012 July 10
This web page describes a simple method for performing "differential photometry" with "transform corrections" (to the Johnson-Cousins standard) for a variable star with at least two calibrated stars in the FOV. The results should be the same as those using classical "transformation equation" corrections. This option to the cumbersome and error-prone transformation equation procedure is made possible by spreadsheets, which are more powerful than old-fashioned log tables and mechanical calculators that were in use when the procedure for transformation equations was developed.
LINKS INTERNAL TO THIS WEB PAGE
Introduction
Example 1: Target w/ several
nearby comp stars
Example 2: Light curve
Example 3: Same target on another
date
Example 4: Different target
on different date
Classical transformation equations
Related external links
Supporting theory
This web page is in response to e-mail inquiries asking for help with
"differential photometry" for AAVSO targets. Although I rarely do DP (as
differential photometry is sometimes referred to), my experience with "all-sky
photometry" (calibrating a target star when there are NO standard stars
in the FOV) allows me to suggest the following simple and novel approach
to conducting DP.
This web page is organized backwards: I first present an example of what
to do, and later present the underlying theory for it. I recognise that
most people just want to know what to do.
EXAMPLE 1: TARGET STAR WITH SEVERAL
CALIBRATED STARS IN THE FIELD OF VIEW
Consider my observations of a target star with 8 calibrated stars in
the FOV, using B- and V-band filters. We want to determine the B and V magnitudes
of the target star transformed to the Johnson-Cousins standard. What should
we do?
There are 3 images with each filter. Let's use MaxIm DL (MDL) for image
processing. After calibrating the B-band images (bias, dark and flat), and
star aligning them, use the Photometry tool to determine "instrumental magnitudes."
The Photometry tool asks for reference stars, so use the 8 stars in the
finder chart (we could also use just one "artificial star" for a better
final result, but let's keep it simple). Each reference star needs a magnitude
so let's use those from the finder chart (again, any old entries will work
using my procedure, but let's go through the motions of using the AAVSO
finder chart "comp star" mag's). Save the Photometry tool's measurements
to a CSV-file. The same is done for the V-band images.
The Excel spreadsheet DP.xlsx should be opened (if you don't have it,
here's a download link for users of Excel 2003 and Excel 2010: DP2003A and DP2010A). It
looks like this:

Excel spreadsheet DP2010.xlsx (2010 version of Excel), used for
calculating "transformed" B & V magnitudes for a target star with nearby
calibrated ("comp") stars.
The above spreadsheet's worksheet shows a 8-step procedure for determining
the target star's "transformed" B and V magnitudes. The light blue cells
indicate user input. Steps 1 & 2 call for importing the B-band CSV-file
to cell B3, and inporting the V-band CSV-file to N3. For steps 3 & 4
manually enter the known true B- and V-band mag's to cells in row 11. Set
the usage cells (row 21) to "1" for columns that have reference stars (this
can be changed later). Now comes the hard part: adjust cells I16 and
I17 for minimum RMS(B), cell K16. There are three ways to do this: 1) manually
change cell values (I16 & I17), 2) adjust the slide bars that do this,
or 3) use the SOLVER tool (not everyone has installed the SOLVER tool; if
you haven't, it's worth doing - check HELP for instructions). After a minimum
RMS(B) has been found, use the same procedure to find a minimum for RMS(V),
using the analogous cells on the right side. That's it! The target star's
B- and V-band magnitudes are displayed in the light yellow cells (E22 &
T22).
The plots show how well the "comp" stars define "star color sensitivity."
If you see one star that's an outlier you can delete it from the calculations
by manually setting the "use" cells (row 21) to zero for the outlier star.
The usage for B and V don't have to be the same.
It was stated above that steps 5 and 6 minimize RMS. Actually, the cell
being minimized is "star flux weighted RMS." Notice that the plot for B has
an outlier (above the fit); this star is faint so it didn't have much influence
on the solution. You can see that it is Ref#3 (note that cell F20 shows this
star's difference with respect to the model fit to be a high -0.030 mag).
A slight improvement in B fit can be accomplished by setting this star's
B-band use cell (F21) to zero.
Keep in mind that the solved-for ZeroShift values are only valid for this image set. On another observing date there can be a difference in atmospheric extinction, and air mass, and this will call for different ZeroShift values. StarColorSensitivity, on the other hand, should be about the same for all observing dates - provided you don't change hardware (focal reducer, filters, etc). Therefore, as an option you can keep track of StarColorSensitivity for each observing date and force the concensus values upon the worksheet (by adjusting cells I17 for B and X17 for V). One way I recommend for establishing StarColorSensitivity is to observe M67 and use the 47 secondary stars that fit within a typical amateur's FOV and which have good magnitude accuracies (link given below).
This worksheet can be used when the filter pair is different from B and
V. If, for example, you're using Rc and Ic, just pretend that all references
to "B" actually refer to "Rc" and all references to "V" actualy refer to
"Ic". Values for StarColorSensitivity will of course differ from occasions
when B and V were used.
I should also note that the spreadsheet can accomodate up to 6 images
and 12 reference ("comp") stars; the user is free to insert rows and columns
to accomodate more images and more comp stars, but if this is done other
cells will have to be modified (anyone with experience with spreadsheets
will be able to figure this out).
EXAMPLE 2: LIGHT CURVE FOR AN OBSERVING
SESSION
The first example is fine when the goal is to determine a pair of B &
V mag's for one epoch. But what about when the observing session consists
of hundreds of image pairs throughout the night, and the goal is to create
of plot of transformed B & V mag's (or just one band) versus time for
the entire observing session?
Notice in the above figure the two transformation corrections for the
target: "TransformationCorr'n for B = +0.034" and "TransformationCorr'n for
V = -0.018" (cells G24 and V24). These "transformation equation" corrections
should be applied to the entire observing session's instrumental magnitudes.
The corrections can be determined from any subset of images (taken at about
the same airmass). When you have a transformation correction for the band
of interest you can then process all images for that band and import the
CSV-file to a light curve spreadsheet. All magnitudes will have to be corrected
by the transformation correction determined above if you want the light curve
to be for "transformed" magnitudes. For this to work, of course, you need
to use the same comp stars (reference stars) that were used for establishing
the transformation corrections.
If your B-band filter produces large values for StarColorSensitivity (e.g., ABS(StarColorSensitivity) > 0.2), and if your airmass values are large (e.g., airmass > 3), then it would be prudent to perform another determination of "transformation correction" for B at a high airmass value. If it differs much from the value at low airmass, then some kind of airmass dependent interpolation should be considered. Probably only B-band will need this additional attention because extinction is high at B-band and this can change the shape of the B-band system throughput at high airmass values.
Once these two "transformation corrections" have been established for
a target star, they can be used for all future observations of that target.
EXAMPLE 3: SAME TARGET STAR ON ANOTHER
DATE
Re-stating the previous sentence: When a target star has been calibrated
using the DP.xlsx spreadsheet, the "transformation corrections" for B and
V can be used on all future (or past) observing sessions. It won't matter
if atmospheric extinction is different (to first order), or what the air
mass differences are (to first order). Refer to the caveat in the previous
section if B-band StarColorSensitivity is large and you're observing
at high airmass values.
EXAMPLE 4: DIFFERENT TARGET STAR WITH
SEVERAL CALIBRATED STARS IN THE FIELD OF VIEW ON ANOTHER DATE
Since only the ZeroShift parameters will change from night-to-night they
are the only two parameters that need to be evaluated each new observing
date. After a few observing sessions in which all four parameters are solved-for
you will have a pretty good estimate of the two StarColorSensitivity parameter
values, and they can be imposed as fixed for other observing sessions. For
example, the above spreadsheet is for a Landolt star field (RA = 06:52)
in which 54 Landolt stars (with 205 star measurements) were used to establish
that StarColorSensitivity = +0.106 ± 0.035 and -0.084 ±
0.032 for B and V, respectively. For other observing sessions these values
can be adopted as fixed. Then when a subset of images (3 to 5 for each band)
is measured and their CSV-files are imported to the DP.xlsx spreadsheet,
only the ZeroShift parameters need to be solved-for. When new ZeroShift values
have been established note the "Transformation corr'n for B" and "Transformation
corr'n for V" (cells G26 and S26). These corrections should be valid
for the rest of the observing session, even though air mass will undergo
changes.
As stated above, when a star has been observed once, leading to a solution for magnitude corrections, these magnitude corrections can be used for all future observing dates of that star.
CLASSICAL TRANSFORMATION EQUATIONS
When I joined AAVSO they sent me a new membership packet, and it included
transformation equations (written by Priscilla Benson: http://www.aavso.org/observing/programs/ccd/benson.pdf
. There was no derivation of them, so I set out to derive them from first
principles. It was sort of fun, especially after noting that my equations
matched those in the AAVSO material, so I created a web page with the derivation:
http://reductionism.net.seanic.net/CCD_TE/cte.html.
But these equations struck me as error-prone and non-intuitive, and the
entire exersize left me thinking that there must be a simpler way to achieve
the same result, that was simpler and more intuitive.
The classical Transformation Equation procedure has limitations (at least
the abbreviated version that's in the AAVSO material does): the coefficients
are limited to use under one atmospheric extinction condition and one range
of air mass values (and one telescope configuration), so they cannot be
expected to perform well under different atmospheric extinction conditions
and different air mass situations (and different telescope configurations).
Professional astronomers employ a rigorous but more complicated set of transformation
equations that explicitly takes extinction into account. The procedure I am
using overcomes the limitations of the simpler transformation equations without
the complication of the rigorous transformation equations. My recommended
procedure is also superior to using classical TE because of the option for
giving greater "weight" to brightyer stars for model solving.
To illustrate that DP is simpler and more intuitive, consider the form
of the CCD transformation equations:
(Vs - Rs) = (Vc
- Rc) + Tvr * [(vs - rs) -
(vc - rc)]
Vs = vs + (Vc
- vc) + Tv * [(Vs - Rs) - (Vc
- Rc)], using the solution for (Vs - Rs)
in the above line
Rs = Vs - (Vs
- Rs), using Vs from the line above, and (Vs
- Rs) from the first line
Bs = Vs + (Bc
- Vc) + Tbv * [(bs - vs)
- (bc - vc)]
where:
Vc = known V-band magnitude of comparison
star,
Rc = known R-band
magnitude of comparison star,
vs = instrumental (i.e., measured and
uncorrected) V-band magnitude of star of interest,
vc = instrumental
V-band magnitude of known comparison star,
rs = instrumental R-band magnitude of
star of interest,
rc = instrumental
R-band magnitude of comparison star,
assuming the following coefficient definitions (unique to an observing system and usually unchanging):
Tv = slope of (V-v) plotted versus (V-R)
Tvr = reciprocal of slope of (v-r) plotted versus
(V-R)
Tbv = reciprocal of slope of (b-v) plotted versus
(B-V)
M67 secondary standards (47 stars): http://brucegary.net/M67/ (useful for
establishing StarColorSensitivity)
AAVSO photometry manual: http://www.aavso.org/ccd-observing-manual
Lou Cohen's 2003 tutorial:
http://www.aavso.org/observing/programs/ccd/ccdcoeff.pdf
Priscilla Benson's (1990's)
CCD transformation equations tutorial: http://www.aavso.org/observing/programs/ccd/benson.pdf
Bruce Gary's CD Transformation
Equations derived from basic princples: http://reductionism.net.seanic.net/CCD_TE/cte.html
Bruce Gary's All-Sky Photometry for Dummies: http://brucegary.net/dummies/x.htm
Bruce Gary's All-Sky Photometry for Smarties - v1.0: http://brucegary.net/photometry/x.htm
Bruce Gary's All-Sky Photometry
for Smarties - v2.0: http://brucegary.net/ASX/x.htm
Bruce Gary's Differential
Alternative Equations: http://brucegary.net/DifferentialPhotometry/dp.htm
Bruce Gary's Astrophotos
home page: http://reductionism.net.seanic.net/brucelgary/AstroPhotos/
Bruce Gary's
all-sky observing session of 2011.10.28 (BVRcIcg'r'i'z', 60 Landolt
stars, 22 SDSS stars): http://brucegary.net/yygem/all-sky/index.htm
Bruce Gary's 2011 version of all-sky observing
and analysis procedure: http://brucegary.net/allsky2011/
Bruce Gary resume: http://brucegary.net/resume.html
[The following material is copied from another of my spreadsheets.
Whereas it was created to explain all-sky photometry most of it is relevant
to differential photometry.]
If the earth didn't have an atmosphere that absorbs starlight then all-sky
photometry would be trivial. The observer would merely take a CCD image of
a region with well-calibrated stars, then another image of the region of
interest with the same settings. Corrections would still be required for the
observing system's unique spectral response, but these "transformation corrections"
would be straightforward since they wouldn't depend on air mass or weather
conditions.
Some observers frequently encounter the need for an accurate magnitude
scale in a region devoid of well-calibrated stars. For example, asteroids
are constantly moving through parts of the sky that do not have nearby well-calibrated
stars. Anyone wanting to determine the BVRI spectrum of an asteroid is "on
his own" for establishing accurate magnitudes for stars near the asteroid.
Novae and supernovae are the most common examples of stars that appear where
there are no well-ccalibrated stars. When a bright one of them is discovered
the AAVSO does a good job of quickly preparing a chart with a magnitude
"sequence" that is based on observations quickly-arranged for by a professional
astronomer (Arne Henden) who uses "all-sky photometry" to establish the sequence.
Not every nova or supernova can be supported this way.
Because of the growing number of amateurs with CCD skills conducting projects
that involve accurate brightness measurements there is a growing need to
explain how to perform all-sky photometry. I have encountered enough situations
where I needed to create my own "photometric sequence" chart that I have been
motivated to learn all-sky photometry techniques. In the process of this
learning I have developed what I believe is a straight-forward method for
all-sky photometry. Maybe it is the same as used by the professionals, but
I'll admit to not having determined this yet.
When I started writing this web page I thought I would try to discourage
amateurs from trying to do all sky photometry. I had many concerns about
the feasibility of an amateur astronomer taking on a task that required sophisticated
observing strategies and data analysis. (This may sound funny, coming from
an amateur, but I spent decades as a radio astronomer and atmospheric scientist,
where I became familiar with atmosperhic extinction and data analysis methods.)
I was especially concerned about the amateur being blindly misled in his
analysis by spatial inhomogeneities and temporal variations of atmospheric
properties (which I had studied before my retirement). I was prepared to
advise amateurs to restrict themselves to "differential photometry," which
is based on a single image of the region of interest. However, while I was
learning to do all-sky photometry for my own projects I developed a procedure
which I now believe makes it feasible for other amateurs to make their own
chart sequences using a version of "all-sky photometry" that I am calling
"Iterative All Sky Photometry." My purpose for this web page has thus changed
from trying to discourage amateur astronomers from doing all-sky photometry
to trying it using a technique that I think is within the reach of many amateurs.
The observer who is impatient may click the link "Observing Strategy" or
"Analysis Procedure" given above. For those wanting some grounding in fundamentals,
however, I begin with a section that reviews atmosphere absorption, as well
as difficulties related to temporal variations and spatial inhomogenieties
of atmospheric properties.
Finally, if your goal is to achieve photometric accuracies no better than
~0.1 mag, I recommend a web page that I prepared for amateurs whose main
interest is asteroid astrometry but who wish to improve over the 1 or 2 magnitude
errors that are commonly prepared by automatic programs (such as PinPoint)
for submission to the Minor Planet Center. This web page can be found at Photometry for Dummies. This
web page is meant for those wanting to achieve 0.04 magnitude accuracy.
Flux
First, imagine that you're out in space, holding a magic "unit surface area" so that it intercepts photons coming from a star. The surface can be a 1 meter square, for example, and its magic property is that it can count photons coming through it for any specified interval of wavelengths, for any specified time interval. Let's give it one more magical property: it can count only those photons coming from a specific star that you designate. We might imagine that this last is achieved by some kind of screen way out in front, having at least the same 1 meter square aperture and located so that the magic surface sees only things from the direction of the star.
This device measures something commonly thought of as brightness, but which astronomers call "flux." Photons of the same wavelength have the same energy, so merely counting photons is equivalent to measureing the energy passing through the magic unit surface. Energy per unit time is power, as in "watts." This magic device measures watts of energy, per unit area, per nanometer of wavelength interval. This is called flux, or a version of flux referred to as Slambda. Let's just call it "S".
Magnitude
If we point our magic unit surface area so that we measure S from one star, then S from another, we'll get two S values: S1 and S2. We can arbitrarily define something called "magnitude difference" according to the following: M2 - M1 = 2.5 * LOG10 (S1 / S2 ).
Let's now arbitrarily assign one star to have a magnirude value of zero.
Then, all stars brighter will have negative magnitudes, and all stars dimmer
will have positive magnitudes. If the flux from that universal reference
star is S0 , then any other star's magnitude will be given by:
Mi = 2.5 * LOG10 (S0 / Si ) Eqn 1
We've now devised a system for describing how many photons pass through a unit surface area, per unit time, per wavelength interval, at a specified interval of wavelengths. And we've arbitrarily devised a dimensionless parameter, called "magnitude," for the convenient statement of that number. Magnitude defined this way is convenient because we don't have to give a long value, such as 1.37e+16 [photons per second, per square meter, between 400 and 500 nanometers]; rather, we can simply say M = 12.62.
But wait, we're not done. The wavelength interval is a crucial part of the measurement, since the measurement will vary greatly as we change wavelength intervals. Let's just call the meaurement for the 400 to 500 nanometer (nm) wavelength region a "blue" magnitude. And we can define "green" magnitudes, and "red" magnitudes, etc, by specifying the wavelength region to be 500 to 600 nm, 600 to 700 nm, etc.
Atmospheric Transmission
Now let's take our magical instrument from outer space down through the atmosphere to the surface of the earth. When we look up, we will count fewer photons. Some of the photons are being absorbed by molecules in the atmosphere, and others are being scattered. The scattering is from two kinds of things: molecules and particles. The molecules scatter in a Rayleigh manner, affecting blue photons most, whereas the particles (also called aerosols) scatter in a way that depends upon the ratio of the wavelength to the circumference of the particle (Mie scattering when this ratio is small, Rayleigh scattering when the ratio is large). At some wavelengths, especially within the "red" band, water vapor molecules absorb (resonant absorption) at specific wavelengths. Ozone molecules also have a preferred wavelength for absorbing photons. For these bands the loss of photons will depend upon the number of water vapor molecules, or ozone molecules, along the line of sight through the atmosphere.
To first order, the loss of photons making a straight line path to the magic unit surface area, located at the surface of the earth, will depend on the following factors:
Blue Rayleigh
scattering by molecules, non-resonant absorption by molecules, scattering
by aerosols
Green Non-resonant absorption
by molecules, scattering by aerosols
Red
Non-resonant absorption by molecules, scattering by aerosols, water vapor
molecules resonant absorption
Let's talk more about the aerosols. They may consist of dust particles, salt crystals that are swollen by varying amounts of absorbed water (these are important at coastal sites), sulphate particles (SO4 molecules stuck together plus with water), volcanic ash in the stratosphere, urban smog, water droplets within clouds, and ice crystals in cirrus clouds. All of these aerosols are capable of presenting angular structure that can pass through a line of sight quickly, such as between the measurement of one star and the next. Even during clear conditions, when the eye cannot see changes in water vapor, the total number of water vapor molecules along a given line of sight can change by a factor of two in less than an hour (personal observation).
The zenith view will usually have the smallest losses. During a typical observing period the entire sky will undergo a uniform rate of change of all of the above factors contributing to loss of photons. Tracking an object from near zenith to a low elevation will cause photon losses to change due to both the increasing amount of air that the photons have to traverse, and due to the changing conditions of the entire air mass in the observer's vicinity. We'll have to come back to this pesky subject later.
If the atmosphere in the observer's vicinity does not change during an observing sesson, then the photon losses will be proportional to the number of molecules and aerosols along the path traversed by the starlight. The losses are exponential, however. Each layer of the atmosphere absorbs or scatters a certain percent of the photons incident at the top of that layer. For example, if the zenith flux is 90% of what it is above the atmopsphere, the 30 degree elevation angle flux (where twice as many air molecules and aerosols will be encountered) will be 90% of 90%, or 81% of the outer space flux. Simple geometery says that:
S(m) = S(m=0) * EXP{-m * tau) Eqn 2
where S(m) is the flux measured for an air mass value "m", S(m=0) is the flux above the atmosphere, "EXP" means take the exponential of what's in the parentheses, and "tau" is the optical depth for a zenith path. Tau, the zenith extinction, can is sometimes assigned units of "Nepers per air mass." (Apologies to astronomers accustomed to seeing air mass represented by the symbol "x"; I'm going touse "m".)
The following figure shows atmospheric transparency for a clear atmosphere with a moderatley low water vapor burden (2 cm, for example).
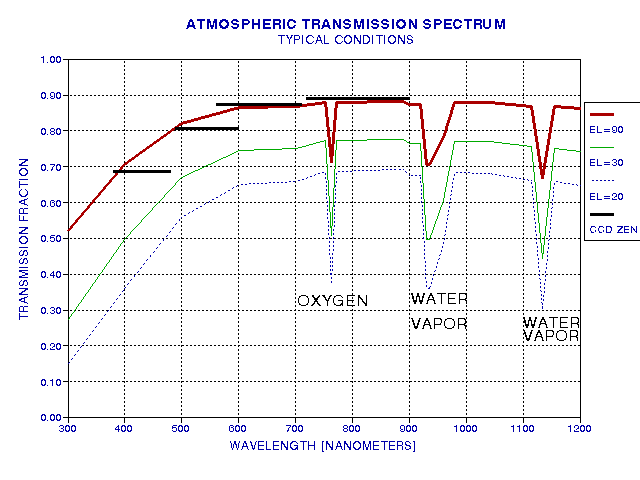
Figure 1. Atmospheric transmission versus wavelength for typical conditions (water vapor burden of 2 cm, few aerosols), for three elevation angles (based on measurements with interference filters by the author in 1990, at JPL, Pasadena, CA). Three absorption features are evident: a narrow feature at 763 nm, caused by oxygen molecules, and regions at 930 and 1135 nm caused by water vapor molecules. Four thick black horizontal lines show zenith transparency based on measurements made (by the author) with a CCD/filter wheel/telescope for typical clear sky conditions on another date and at another location (2002.04.29, Santa Barbara,CA, SBIG ST-8E, Schuler filters B, V, R and I).
Since zenith extinction changes with atmospheric conditions differences of several percent can be expected on different days. In Fig. 1 the transparency in the blue filter region (380 to 480 nm) differs by ~10% between the two measurement sets. Changes of this order can occur during the course of a night. This may be an unwelcome thought, but it is a fact that careful photometry must reckon with (discussed below).
At my new observing site in Southern Arizona (4660 feet elevation) I have
measured the following extinction constants (2004.10.15):
B = 0.28 magnitude/air mass, or 77 % zenith
transmission
V = 0.16
" or 86
% "
R = 0.13
"
or 89 % "
I = 0.09
"
or 92 %
C = 0.13
"
or 89 % "
(i.e., unfiltered)
Unsurprisingly, a medium-high altitude site in Southern Arizona has less
extinction thatn a coastal site in Southern California.
Hardware Spectral Response
The concept of "spectral response" is important throughout all that is dealt with here, so let's deal with that now. Consider a single observation (or integration) of a field of interest using a single filter. The term"spectral response" refers to the probability that photons of light having different energies (wavelengths) will successfully pass through the atmosphere (without being scattered or absorbed) and pass through the telescope and filter and then be registered by the CCD at some pixel location. This probability versus wavelength, called spectral response, varies with photon wavelength, ranging from zero at all short wavelengths, to maybe 20% (as described below) near the center of the filter's response function, and back to zero for all longer wavelengths. The spectral response will be a smooth function, having steep slopes on both the short-wavelength cut-on and long wavelength cut-off sides of the response function. The entire journey of a photon through the atmosphere, the telescope, the filter, and it's interaction with the CCD chip, where it hopefully will dislodge an electron that will later be collected by the CCD electronics when the integration has finished, can be summarized by "probability versus wavelength" functions, described next.
Assuming the observer is using a reflector telescope, or a Schmidt-Cassegrain with small losses in the front glass corrector, the photon that makes it to ground level has a lossless path through the telescope to the filter. For observers using a refractor telescope, there may be losses in the objective lens due to reflections and absorptions. For a good objective, though, these losses will be small. The remainder of this section deals with what happens to ground-level photons that reach the filter.
Filter Pass Bands
There are two commonly used UBVRI filter response "standards" in use, going by the names Cousins/Bessell and Johnson. Most amateurs use filters adhering to the Johnson response shape. The two systems are essentially the same for UBV, and differ slightly for the R and I filters. Observations made with one filter type can be converted to the other using the CCD transformation equations, so it would be wrong to say that one is better than the other. The choice of one system over the other is less important than a proper use of either one (as Optec forcefully states on their web page). Even filters from different manufacturers differ slightly from each other. The following figure shows a typical filter response for BVRI filters made by Schuler.
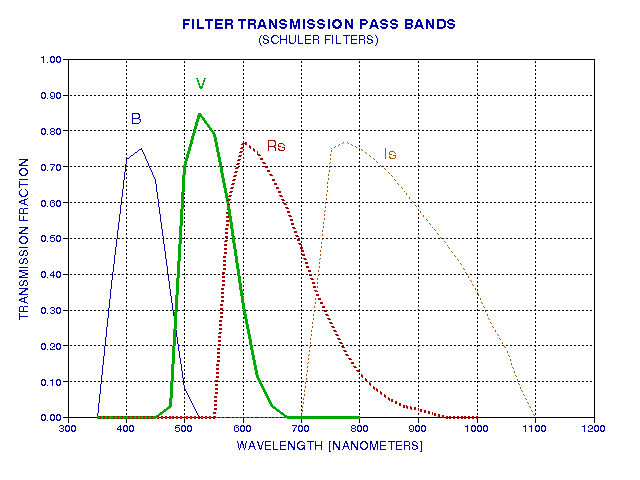
Figure 2. Spectral response of a set of photometric quality
filters.
Considering those 500 nm photons coming in from a 30 degree elevation, for which only 67% make it to ground level, they may have another 70% probability of passing through the V-filter, for example. In other words, only 47% of photons at the top of the atmosphere and coming in at a 30 degree elevation angle make it to the surface of the CCD chip.
CCD Chip Quantum Efficiency
Photons that make it through the atmosphere and filter still must reach the CCD chip if they are to register with the observer's image. There's a matter of cover plates, protecting the chip and preventing water vapor condensation, which is a minor obstacle for a photon's journey. The real challenge for photons is to deposit its energy within a pixel part of the CCD chip and dislodge an electron, setting it free to roam where it can be collected and later produce a voltage associated with the totality of electrons collected at that pixel location. The fraction of photons incident upon the CCD that can produce electrons in a collection "well" is the CCD's quantum efficiency. The quantum efficiency versus wavelength for a commonly used CCD chip is shown in the next figure.
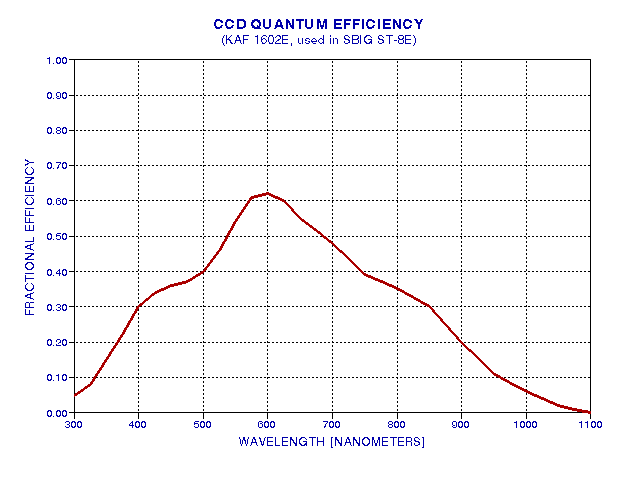
Figure 3. Fraction of photons incident upon chip that free electrons for later collection (KAF 1602E chip, used in the popular SBIG ST-8E CCD imager).
Considering again 500 nm photons, of those that reach a typical CCD chip, such as the one used in SBIG's ST-8E, only 40% dislodge an electron for later collection and measurement. For the V-filter, therefore, only 19% of those photons at the top of the atmosphere, coming in at 30 degrees elevation angle, actually get "counted" during an integration under typical clear weather conditions. This number is the product of three transmission functions given in the above three figures. Each filter has associated with it a total transmission probability, and it depends upon not only the filter characteristics, but also upon the atmosphere and the CCD properties. For the system used in this example, the following figure shows the spectral response for photons arriving at a 30 degree elevation angle, under typical weather conditions, going through Schuler filters and being detected by the KAF 1602E CCD chip.
Spectral Response Due to All Sourcse of Photon Loss
The following figure shows the fraction of photons starting at the top of the atmosphere that can be expected to contribute to a star's image for a typical atmosphere conditions, using typical filters and a commonly used CCD.
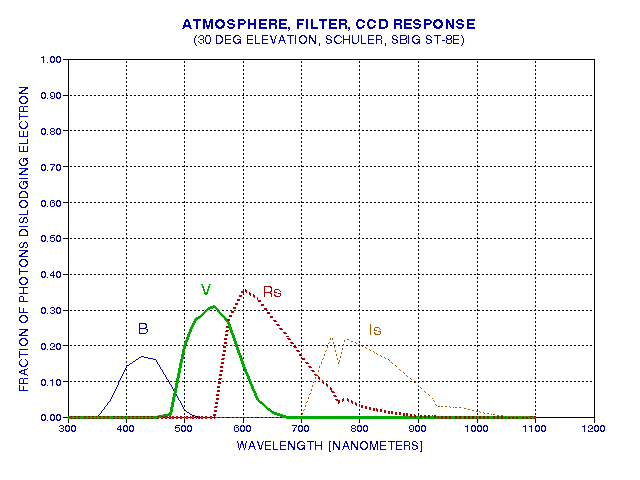
Figure 4. Response of entire "atmosphere/filter/CCD system" for typical water vapor burden, few aerosols,30 degree elevation angle, Schuler filters and SBIG ST-8E CCD (KAF 1602E chip).
The reader may now understand how it happens that different observers can have different system spectral responses for their specific systems and atmospheric conditions. Two observers may be making measurements ar the same time from different locations and using different filters and CCD imagers, and unless care is taken to convert their measurements to a "standard system" their reported magnitudes would differ. The magnitude differences will depend upon the "color" of the star under observation, as described in the next section.
Different Observers Have Different Pass Bands
To illustrate the fact that different observers can have different pass bands when they're both making B-filter measurements, let's consider two observers working side-by-side but using different filters and CCD. For example, before I purchased a SBIG ST-8E with Schuler filters, I used a Meade 416XTE CCD with their RGB filter set. The Meade B filter was intended for RGB color image creation, not for photometry. Since the filters weren't designed for photometry (as Meade acknowledges) they will require large corrections during the process of converting observations made with them to a standard system. For the purpose of this discussion, illustrating the concepts of filter differences, the Meade 616 filters provide are suitable example of the need to be careful. The next figure shows the "atmosphere/B-filter/CCD" spectral responses.for the two systems under consideration.
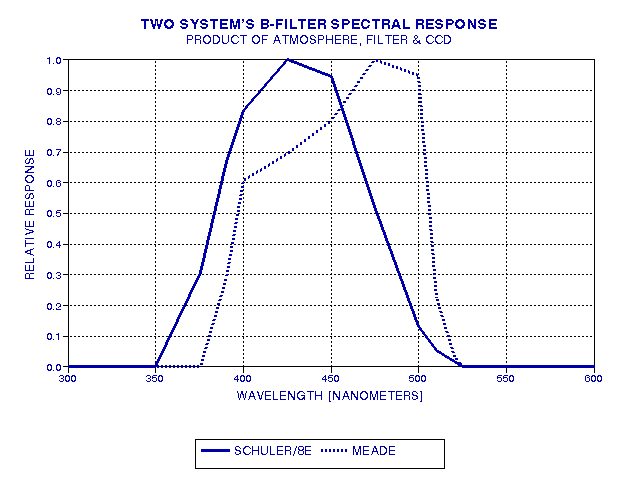
Figure 5. Spectral response of different systems. The solid trace consists of a Schuler Bu filter, intended for photometry, and a SBIG ST-8E CCD, whereas the dotted trace is for a Meade B-filter and 416XTE CCD. The response for both systems corresponds to observing at an elevation angle of 30 degrees in a typical, clean atmosphere (2 cm precipitable water vapor). Both response traces are normalized to one at their peak response wavelength.
The Meade system has a spectral response that is shifted to longer wavelengths compared to the Schuler/SBIG ST-8E system. This shift may not seem like much, but consider how important it can be when observing stars with a spectral output that usually is falling off at shorter wavelengths throughout the wavelength region of these filter pass bands. The next figure shows a typical star's brightness versus wavelength.
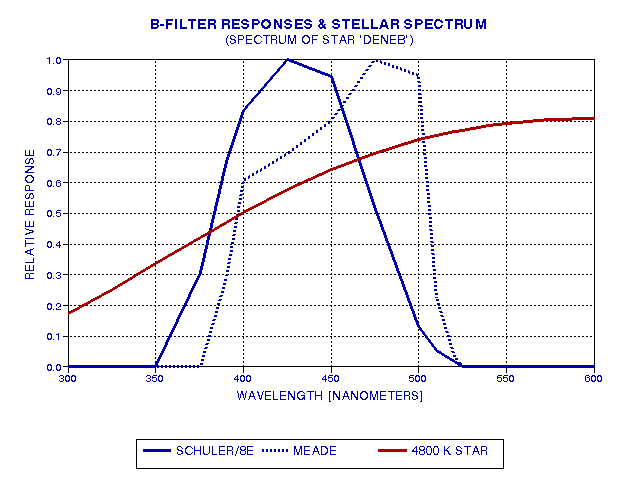
Figure 6. Spectrum of a typical star, Deneb, having a surface temperature of 4800 K, in relation to the two system's B-filter spectral responses.
When a typical star (such as Deneb, shown in the figure) is observed by both systems, the Meade system is observing "higher up" on the stellar brightness curve, producing a greater spectrum-integrated convolved response than for the Schuler/8E system. (The "spectrum-integrated convolved response" is the area under the curve of the product of the stellar source function with the filter response function.) For example, the ratio of spectrum-integrated convolved responses in this example is 1.137, corresponding to a magnitude difference of 0.14. In other words, the Meade system will measure a blue magnitude for Deneb that is too bright by 0.14 magnitudes, and whatever correction algorithm is used should end up adding approximately 0.14 magnitudes to the Meade system's B-magnitude. Redder stars will require greater corrections, and bluer stars will require smaller corrections.
Corrections of this amount are important, which illustrates the need for going to the trouble of performing CCD transformation equation corrections. Observers using filters intended for photometry use will presumably require smaller corrections than the 0.14 magnitudes of the example cited here. Since it is reasonable to try to achieve 0.03 magnitude accuracy, corrections for filter and CCD differences are an important part of the calibration process.
To the extent that the atmosphere can change the spectral response of an observer's atmosphere/filter/CCD for any of the BVRI configurations, it may be necessary to somehow incorporate "atmospheric extinction effects" into the data analysis procedure in order to assure that magnitude estimates are high quality. For example, Rayleigh scattering grows as the inverse 4th power of wavelength, so high air mass observations will shift the short wavelength cut-on of the blue filter more than the same filter's long-wavelength cut-off. In effect, high air mass observations are being made with a blue filter that is shifted to the red. The effect of this will be greater for red stars than blue stars. A simple method is described in a later section of this web page for performing a first order correction for atmospheric extinction effects.
Extinction Plot Pitfalls
The next pair of figures show what will happen when losses (absorption
plus scattering) vary linearly with time. For simplicity, I have neglected
spatial inhomogenities, which are also going to be present when there are
temporal variations. First, consider a plot of the log of intensity versus
air mass when the atmosphere does not change.
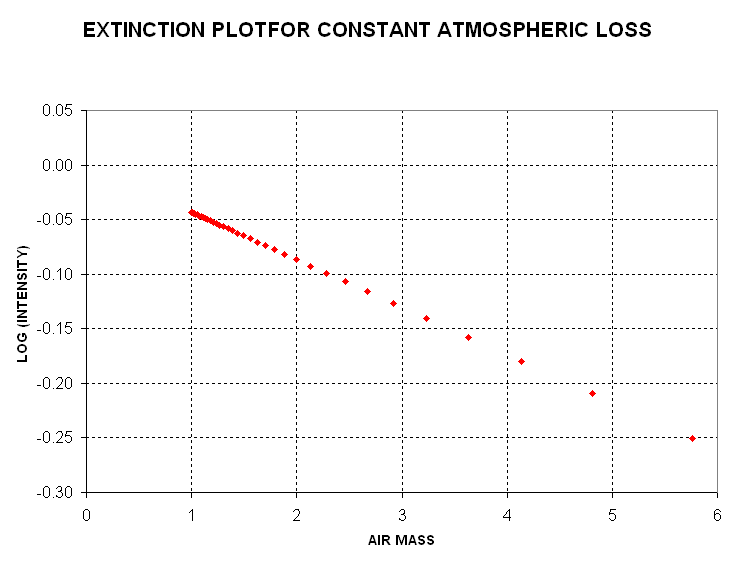
Figure 7. Extinction plot for constant atmospheric losses. It is assumed that Log(I) outside the atmosphere is 0.00 and that each air mass has a loss of 0.1 Nepers (optical depth = 0.1).
An "extinction plot" uses log of measured intensity plotted versus air
mass. If the Y-axis were simply "intensity" then perfect data plots would
be curved; using Log(I) produces straight line plots, which simplifies analysis.
In the above plot the modeled data has a slope, defined as dLog(I)/dm, of
-0.45. The slope is a dimensionless quantity, and it should be the same for
all stars (havng the same spectrum) regardless of their brightness. A slope
of -0.045 corresponds to a transmission of 90% per air mass (i.e.,
10 raised to the power -0.045 = 0.90). Another way of describing this situation
is to state that extinction amounts to 0.11 magnitude per air mass (i.e.,
2.5 * Log (0.90)). Thus, for a view where m=1 the observed star intensity
is 90% of its outside the atmosphere value, at m=1 it is 81% (90% of 90%),
etc. This is a typical extinction value using a V-filter under good sky conditions.
Now consider the same plot but for a linearly temporal change in atmospheric
loss, as might occur when an air mass transition is in progress.
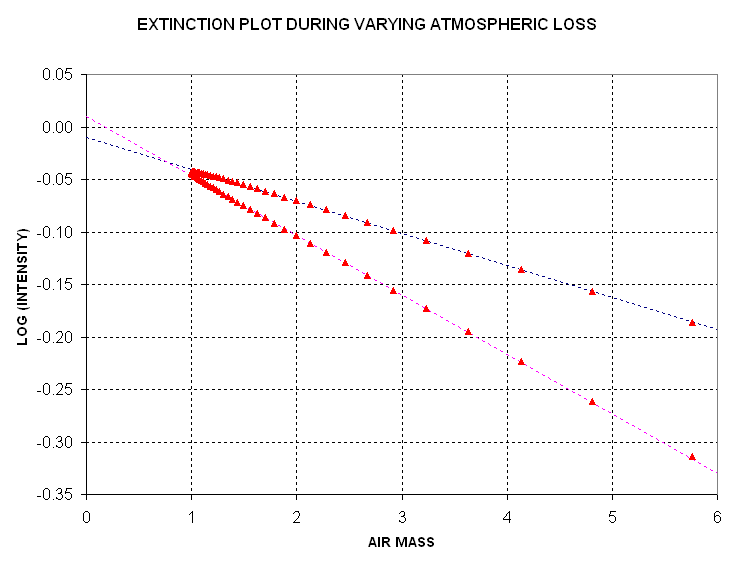
Figure 8. Extinction plot for temporally varying atmospheric
losses. The dashed lines are fitted to rising and setting portions
of the measured intensity.
I've seen this double-branched extinction plot many times during my studies
of atmospheric extinction. One branch corresponds to the rising portion of
data and the other corresponds to the setting portion. If intensity measurements
are made during only one of the branches then a fitted slope would imply
an incorrect extinction per air mass value.
Several properties of the atmosphere can contribute to temporal changes in atmospheric transmission. Sub-visible cirrus (just below the tropopause) that is present in one air mass but not its surroundings is probably the most common source. Volcanic ash can be present above the tropopause (in the lower stratosphere). Volcanoes also eject SO gas, which combines with water vapor to form sulfate aerosols, and these also will be distributed in a non-uniform manner.Water vapor in the lower troposphere is almost always undergoing change at a given site. Vapor burdens (the vertical integral from the surface to the top of the atmospehre) can vary from 1 cm to 6 cm (precipitable water vapor), and I have documented factor of two changes during a half-hour interval at a site in Pasadena, CA. Smog is found near urban sites and the associated aerosols can contribute to large changes in atmospheric transmission. Clearly, some sites will be more prone to these atmospheric transmission changes than other sites. Coastal and urban sites will be worse, generally, but even desert sites will experience some fo the above sources of atmospheric change.
This serves to illustrate that careless observing strategies can produce
extinction plots with misleading slopes, and the slopes are used to derive
atmospheric extinction (Nepers of loss per air mass, or optical depth per
air mass).
I can think of a couopleways to deal with an atmos[phere that is varying
with time. First, restrict all observations to a small air mass range while
alternating between the ROI and standard star fields. Second, alternate
observations of standard star fields that are rising and setting. If this
second approach is used the two stars will exhibit discrepant slopes for
the same air mass region, and this will allow a determination to be made of
the temporal trend as well as an extinction value for the approximate midpoint
of the observations.
I don't want to describe more details of how to process extinction plots
when trends exist, for my purpose here is to simply sensitize the all-sky
photometrist to a problem that is easily overlooked.
This Fundamentals section has described the reasons all-sky photometry
is a challenging task, and I hope it has sensitized the prospective all-sky
observer to the importance of doing it carefully. The next section will give
specific observing strategies that I have found useful in performing all-sky
photometry.
Planning! Before every night's observing session I formulate a plan. This
is especially important for all-sky photometry. Every observer will have
their preferred procedure, but each procedure should address the issues raised
in the previous Fundamentals section. In this section I'll present my preferred
way of all-sky observing.
Assume there's just one "region of interest" (ROI) where a photometric
sequence is to be determined. I use TheSky 6.0 to make a list of the ROI's
elevation versus time. The preferred time to observe is when the ROI is at
the highest elevation, but this is not always possible. For us poor people
who mistakenly bought a German equatorial mount telescope, there's a big
penalty for crossing the meridian. A dozen things have to be changed after
a "meridian flip" and the data on each side of the meridian are not guaranteed
to be compatible. I NEVER do all-sky photometry with my Celestron CGE-1400
using data from both sides of the meridian. In fact, I always observe on just
one side of the meridian the entire night, photometry or not, and thus avoid
the nuisance of all that "meridian flip" routine. (I'll never buy another
GEM, never! For my diatribe against German equatorial mounts for photometry,
go to http://brucegary.net/CGE/x.htm)
After deciding on the range of time (and elevation) for the ROI observations,
groups of well-calibrated standard stars can be chosen. The guideline for
this is to observe standard stars in such a way that they are observed throughout
the same range of elevations as for the ROI. I try to include at least at
least one group as close to zenith as possible and another as low in elevation
as possible. In addiditon, I try to include groups of standard stars at the
beginning and end of the night's observing session athat are at the same
elevation, preferably near the ROI's low elevation range. This choice will
be useful in assessing the existence of temporal trends.
With TheSky displaying in the "horizon" mode it is easy to see which stars
are at elevations of interest. I often use the Landolt list of well-calibrated
stars for my primary calibration. The Landolt list contains 1259 stars in
groups that are mostly along the celestial equator, as shown in the follwoing
figure.
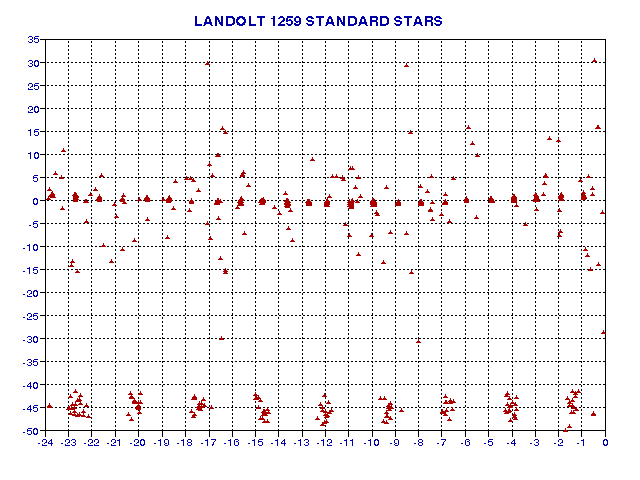
Figure 9. Locations of Landolt stars. Declination
[degrees] is the Y-axis and RA [hours] is the X-axis. (Note that RA shows
a negative sign, due to a limitation of my spreadsheet program.)
TheSky is able to display this list of stars (with whatever symbols you like) by specifying the Landolt text file's location in the Data/SkyDatabaseManager menu. You can download this Landolt text file from LandoltTextFile.
Since none of the Landolt stars go through my zenith I also depend on
Arne Henden's set of sequences (constructed mostly for the AAVSO, I suspect).
His data can be found at Arne1
and Arne2.
A third source for standard stars is the large database maintained by
the AAVSO. You first have to pick a star that's in the AAVSO chart database
and then download a chart for it. Not all charts are good quality, and only
a few have more than just V-magnitudes, so this data source is inconvenient
Example Observation Session
To illustrate the procedure I use for all-sky photometry I will use an
observing session conducted June 19, 2004 (UT). A Celestron CGE-1400 telescope
was used with a SBIG ST-8XE CCD at prime focus, using a Starizona HyperStar
adapter lens. Custom Scientific B, V and R photometric filters were used.
All images were made with the CCD cooled to -10 C. Focus adjustments were
made several times during the 3-hour observing session. When I'm using a
prime focus configuration the Custom Scientific filters are not parfocal,
and this required that I refocus for each filter change. I used a table of
previously-determined filter focus offsets. Sky conditions were "photometric"
and based on atmospheric seeing of the past few nights and the recent reliability
of ClearSkyClock seeing forecasts for my site, I suspect that the seeing afforded
FWHM ~ 2.3 "arc (for a Cassegrain configuration). The prime focus configuration
produces a "plate scale" of 2.8 "arc/pixel, and due to slight distortions
caused by an imperfect prime focus adapter lens I was able to achieve FWHM
of no better than 7.5 "arc. I at least covered a large field of view, 72
x 48 'arc, using a "fast" system, f/1.86.
The purpose for the June 19, 2004 observing session was to establish a photometric sequence for a cataclysmic variable that had been recently discovered as a suspected nova. The object has a designation of 1835+25 (plus a temporary designation of VAR HER 04). This outbursting binary star is located in the constellation Hercules (about a minute of arc from the border with Lyra), at 18:39:26.2, +26:04:10. The magnitude for the June 19 observations was ~12.7.
The following figure is a screen shot of TheSky ver. 6.0 showing how two
Landolt star groups and one Arne Hendon sequence (for an AAVSO blazar) were
selected for use to calibrate a star field near the new nova, labeled "Nova
2004".
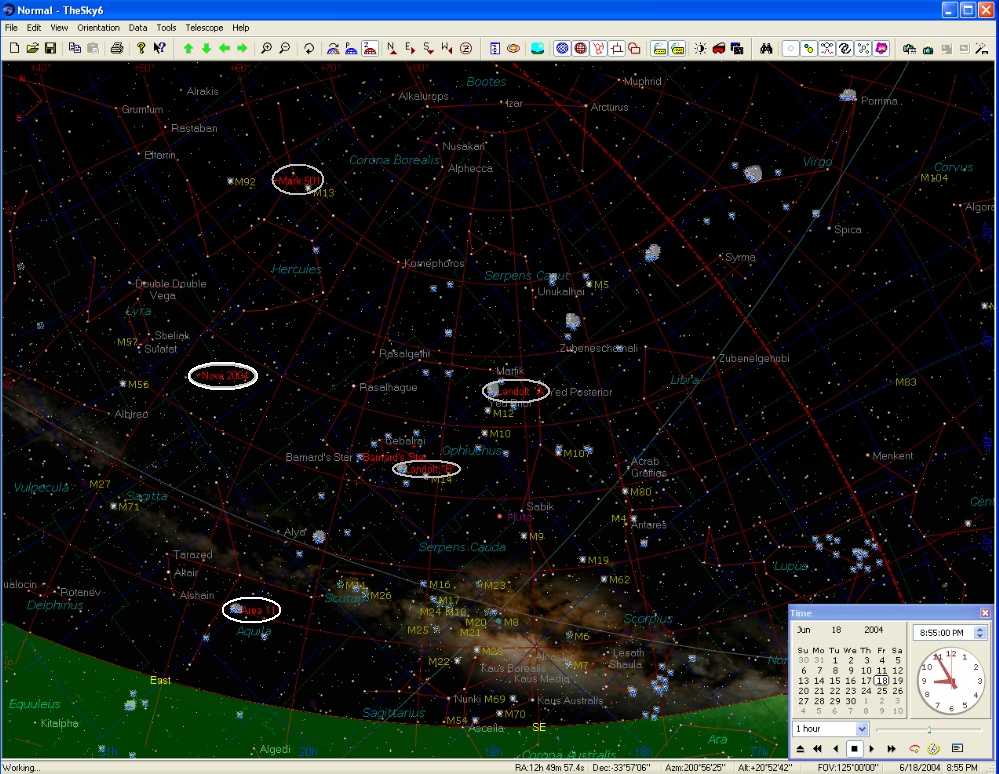
Figure 10. Resized and compressed screen shot of TheSky
in horizon display mode showing the region of interest ("nova 2004", within
middle-left oval), two Landolt star groups (middle-right ovals), Area 111
(lower-left oval, containing Landolt stars) and an AAVSO chart with Arne
Henden calibrated stars (top-left oval). Other Landolt star groups are shown
by the blue symbols. The meridian is shown by a red dashed trace from the
lower-right horizontothe top-middle border. Elevation isopleths are shown
by thin red traces parallel to the horizon. (The reduced size, compression
and conversion to JPEG greatly degrades readability, made necessary to keep
the file size reasonable.)
Other "planetarium" display programs can probably also be used to select
standard stars (but the TheSky is a great deal and has all the features any
CCD photometrist would want).
After selecting the groups of standard stars to be used as a primary magnitude
standard an observing schedule should be decided upon. Recall the two strategies
described briefly in the previous section for dealing with slowly varying
extinction: 1) restrict all observations to a narrow range of elevations
and alternate observations of standard star regions with the ROI, and 2) alternate
observations of standard star fields that are rising and setting and determine
the trend as well as an average extinction value that can be used with the
ROI observations (made later, earlier or during the standard star observations).
Since my telescope is on a German equatorial mount the second option is
not feasible. Therefore, I always employ the first strategy for dealing with
the possibility of extinction trends during an observing session. For the
observing session being used as my example I decided to start out observing
the "Landolt A" group (right-most oval) and then the ROI (lower-left oval).
This timing places the two targets at about the same elevation, and closely
spaced in time, which means that this pairing will be unaffected by later
assumptions about temporal extinction trends and extinction values. This
is a conservative strategy, and it assures that something useful could be
done with just the first two targets (in case of equipment problems or other
show-stoppers prevented later targets from being observed). It may not have
been the best strategy, but for this observing session I then observed Markarian
501 (upper-left oval), the ROI, Landolt A, and continued through that cycle
until one of the targets reached the meridian, then an observation of Area
111 at a low elevation (since it rose late in the night's observing).
Notice that the first Landolt A standard stars and the Area 111 standard
stars are to be made at about the same elevation and are at the beginning
and end of the night's observing session. This makes them an ideal pair for
assessing any trend in extinction value.
My observing plans included a list of things to do before dark. For example,
review the previous observing session log notes to recall if anything anomalous
occurred, review which filters are in the filter wheel (I have a SBIG "pretty
picture" set and a photometric set), review the CCD settings that were last
used (hardware present, flip values, image scale for proper centering), review
the adequacy of the last pointing map, and determine if any telescope reconfiguration
and rebalancing will be needed. For this specific observing session I had
to reconfigure from Cassegrain to prime focus using the Starizona HyperStar
field flattening lens, and this had to be done before dark. This also requried
a rebalance and an approximate refocus using nearby mountains (so that the
flat fields would be at the correct focus setting). I also had to replace
some "pretty picture" filters with photometric filters. My plan had to include
new flat fields shortly after sunset, for each filter, and a completely
new pointing calibration (using MaxPoint). Every reconfiguration and rebalance
requires a new pointing calibration. The plan called for setting the CCD
cooler to a value that could be established quickly (such as +5 degC), prior
to the flat field images of the zenith sky after sunset. The plan also included
a sequence of targets, as well as the brightest star to be included in the
analysis (needed for establishing an exposure time that does not lead to
"saturation" of the brightest star). Users of MaxIm DL 4.0 will recognize
some the tasks listed above. That's the hardware control and image analysis
program that I use.
All pre-target items on the plan were implemented before sunset. After
the flat fields were complete I cooled the CCD as far as possible. I determined
that the night's CCD cooler setting would be -10 degC for the entire night,
since that's as cold as I could get without exceeding a cooler (TEC) duty
cycle of 90%. For all-sky photometry it's absolutely essential to use the
same CCD cooler setting the entire night, and to periodically check that
the cooler duty cycle is not approaching 100% (due perhaps to a warming that
could be caused by sundowner winds for example).
I observed each target field with the B, V and R filters. Each filter had
to be focused differently since my photometric filters are not "parfocal"
when at prime focus (the pretty picture filters are parfocal). An exposure
time had to be determined for use on all targets. This probably isn't necessary,
but that's my current preference. A long exposure would cause saturation
for the brightest stars, rendering them unuseable for photometry. I decided
upon an exposure time of 10 seconds after quickly studying the first V-filter
exposure of a star field with known magnitudes.
While observing I keep an "observing log" with an ball point pen. After
observations have terminated I use only a pencil to add comments based on
recollections. This ink/pencil distinction can help in reconstructing what
really happened months later if a re-analysis or review of the observations
is made. For each exposure sequence I note such things as UT start time,
object, filter, exposure time, guided (by AO-7 image stabilizer) or unguided,
focuser sensor temperature (taped to the telescope tube), outside air tempreature,
wind speed and direction, and sometimes my impressions of data quality as
I calibrate and review images coming in "on the fly." When a focus
sequence is performed I log the focus setting and 6 FWHM readings for a sequence
of focus setting valeus centered on the expected best focus position. As
soon as this set is completed I plot FHWM for the best 3 of each set
of 6 FWHM readings, and do a hand fit trace to establish the best focus setting.
I note what the best FWHM value is for the focus sequence, and use that as
a reference to monitor drift away from best focus during later imaging in
order to determine when a new focus sequenmce is needed.
On this occasion, June 19, all standard star fields and the ROI were observed
successfully. Depending upon how tired I am I try to begin data analysis
shortly after observations are completed. Invariably, data analysis is best
done as soon after observations as possible. The memory of odd occurences
and other impressions fade with time, and during analysis all these extra
memories are potentially helpful.
Differential photometry with MaxIm DL can be done manually or with a photometry
tool. The photometry tool is preferable because it rejects outliers in the
sky reference annulus. However, for all-sky photometry the needed measurement
is "intensity", and this is not recorded by the photometry tool. (If you're
not using MasxIm DL and your image analysis program doesn't display intensity
as you move the 3-circle pattern over the image, then buy MaxIm DL or a program
that does display intensity.) Therefore, manual readings are required for
each star to be included in the analysis.
It is absolutely necessary to use the same signal aperture size for ALL
manual readings of intensity for an entire all-sky observing session. Small
changes in the sky reference annulus are OK, as are small changes in the
gap annulus - but give careful thought to the signal aperture size before
starting to measure and record intensities.My suggestion is to use the fuzziest
image that you're convinced you need to use and select a signal aperture radius
of ~1.5 times the FWHM of a star that has a signal-to-noise ratio (SNR) within
the range 50 to 300. Be certain that the FWHM is for a star that is not saturated
(i.e., that has a maximum counts value less than 40,000).
Raw images should be calibrated using the appropriate dark frames. Flat
frame calibration should also be applied to all images. For each field and
filter and observing sequence, a median combine should be performed...
Star Intensity Readings
When making readings of intensity there is the matter of how to position
the aperture circles. For bright stars (SNR > 50, for example) I use the
position that yields the greatest intensity. For fainter stars I manually
position the aperture circles so that brightest pixels are at the center
of the signal aperture circle. Often a greater intensity reading occurs at
one of more pixels away from this setting, but that is usually due to the
sky reference annulus including a slightly different set of pixels and random
noise can change the sky reference level depending on which pixels are included
in the sky reference annulus. This effect is unimportant for bright stars,
but it can dominate intensity results for faint stars.
Intensity readings are made for all Landolt (and other) standard stars,
as well as a selection of stars in the ROI. These should be noted in a reduction
log (using pencil). Intensity is defined to be the sum of all "extra" counts
within a signal circle, where "extra" means differences with respect to the
average count value within a sky referecne annulus. The sky reference annulus
is separated from the signal circle (aslo called an aperture circle) by
an annulus shaped gap, which allows the signal circle to be kept as small
as possible while preventing the sky reference annulus from "contamination"
by starlight from the star in the signal circle.
Extinction Determination
After all stars have their intensity measured for all images the next step
is to determine an atmospheric extinction for each filter. Considering each
filter in turn, and determine the air mass range for each field. Probably
it is best to choose the field with the greatest air mass range for determining
extinction, for each filter (note: it's OK to use the ROI with unknown star
magnitudes for this purpose). When a star field has been chosen for determining
extinction for a given filter the measured intensities should be entered
into a spreadsheet program (such as Excel).

Figure 11. Extinction plot for one field of stars (the ROI) for
R-filter measurements. Each intensity measurement was converted to "2.5 *
LOG(Ir)" before it was plotted. The slope for each fitted straight line is
-0.19 "2.5 * LOG(Ir)" units per air mass, which was the best fit.
The graph shows that one slope [having units of LOG(I) per air mass],
with offsets for each star, fits all extinction plotted data. A best fit
slope value can be determined by a variety of techniques. I find it useful
to enter trial values for extinction, K [mag/m] or magnitude change per air
mass, into a cell in the spreadsheet and note the average RMS residual fit
between a least squares fit model and all measurements. Each time an extinction
value is entered the spreadsheet calculates a best fit intercept for each
star (using K*mav and sum of 2.5*LOG(I) /N, where N is the number of air
mass obserations and mav is the average air mass; details left to the student).
This "trial and error" procedure is a manual least squares solution for K,
and it should be performed for each filter. Afterwards, there will be a
set of K values for each filter, such as 0.25, 0.20 and 0.15 [mag/m], corresponding
to the magnitude change per air mass for B, V and R filters.
Extinction Trends Evaluation
So far this procedure has not allowed for a determination of extinction
trend. Since the June 19 observing date was planned to have negligible effect
from extinction trends it is not necessary to evaluate it. However, for the
purposes of this web page let us do this using the first and last standard
star fields that were observed at about the same air mass. Since B-filter
measurements experience the greatest level of extinction the B-filter data
can be expected to show a greater effect than the other filter data. However,
for this particular data set there are no pairs of osbervations separated
by a large time span that are at the same air mass. The V-filter data comes
the closest to having similar air mass measurements with a large time span
separating them, so that's the data I'll analyze for an extinction trend.

Figure 12. Deviations from extinction model that has no extinction
trend for V-filter observations of Area 111 (m=1.55) and Landolt A (m=1.40)
taken 1.8 hours apart.
The two sets of V-filter measurements appear to fit the same model for
converting intensity, B-V color, extinction and air mass to V-magnitude.
The two data groups deviate from this single extinction model by 0.012 +/-
0.030 magnitude. Taking into consideration their average airmass of 1.47,
and the 1.8-hour time span separating them, the two groups of data imply an
extinction trend of 0.004 +/- 0.011 [magnitude per air mass per hour]. This
is statistically insignificant, and the trend, even if it were real, would
be 3.0 +/- 7.6 [%/hour] decrease in the average 0.15 [magnitude/air mass]
extinction value. Even if this extinction trend were real it would produce
V-magnitude errors of +0.008 +/- 0.020 at one end of a 3-hour observing interval
and -0.008 +/- 0.020 at the other end of the observing interval (for an
average air mass of 1.33). Uncertainties at this level are small compared
with the other uncertainty components, so it is legitimate to assume that
extinction was not changing during this particular observing session.
Converting Intensity to Star Magnitude Using Standard Stars
It is intuitively reasonable to think that a star's measrued "intensity"
(as defined above) contains information about its brightness. Consider the
simplesst possible plot of this, using well-calibrated standard stars, in
which Intensity is plotted versus true magnitude. The following data is from
an observing session on October 15, 2004, and includes 3 Landolt areas with
a total of calibrated 80 stars.
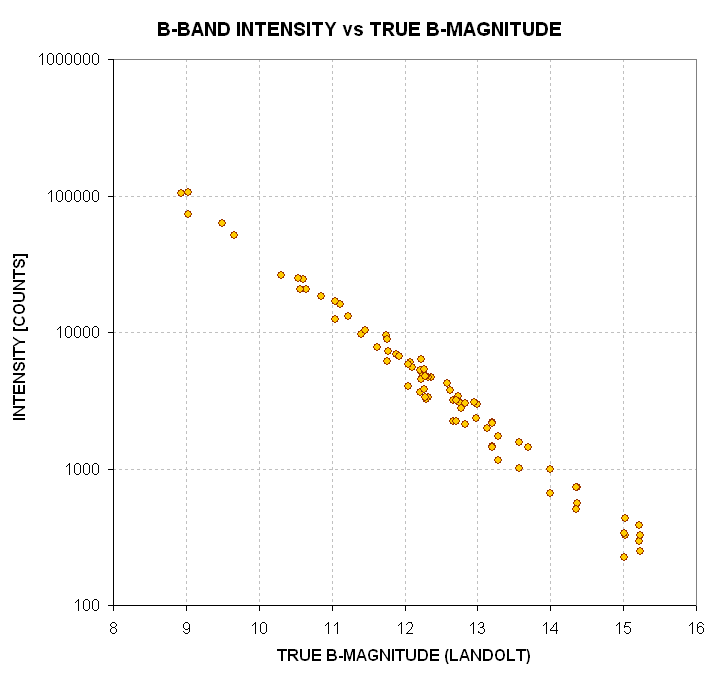
Figure 13. Measured intensity of standard stars in B-filter images
for 80 Landolt stars (2004.10.15).
Indeed, the intuitive idea that measured intensity is related to true V-magnitude
is borne out by this graph. The graph suggests that we should plot the LOG
(to base 10) of measured intensity versus true B-magnitude. In fact, if we
plot 2.5 times LOG(1/Intensity) we should have a parameter that is closely
related to magnitude, subject to the same offset for all stars.
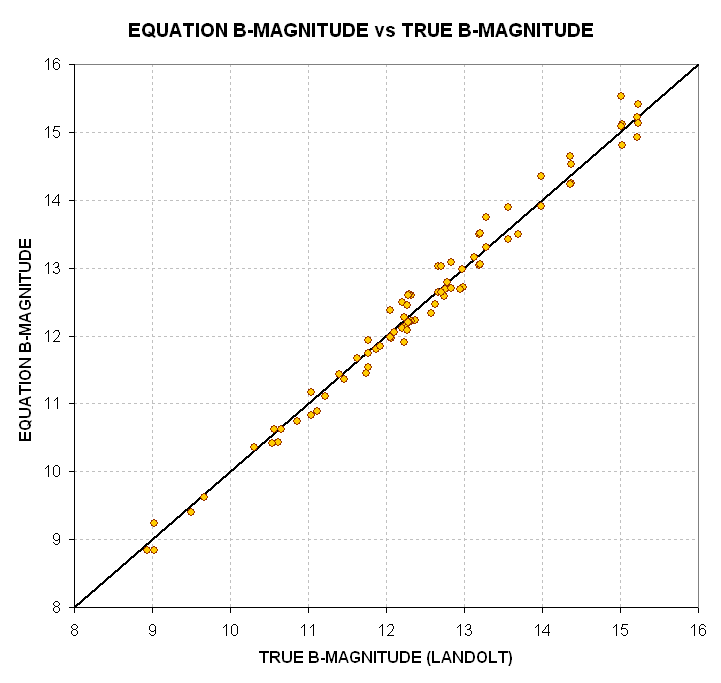
Figure 14. Plot of 2.5 * LOG(Iv) +18.9 (arbitrary offset), labeled
"EQUATION B-MAG" in the graph, using the measured intensities (Ib) of standard
stars in B-filter images.
Sure enough, by playing with arbitrary offsets it was possible to find
an offset value (+19.8) that affords a fairly good correlation of converting
"2.5 * LOG(10/Ib) plus offset" with the true B-magnitudes of the standard
stars. This equation doesn't take into account the different air masses of
the various images from which intensity measurements were made, nor does
it take into account the different colors of the standard stars. The colors
should matter since the observing system has a unique spectral response (caused
by the corrector plate, prime focus adapter lens, filters and CCD response,
as well as the atmosphere). Let's plot the deviations of the above measurements
from the fitted line and see if these differences correlate with air mass
and star color.
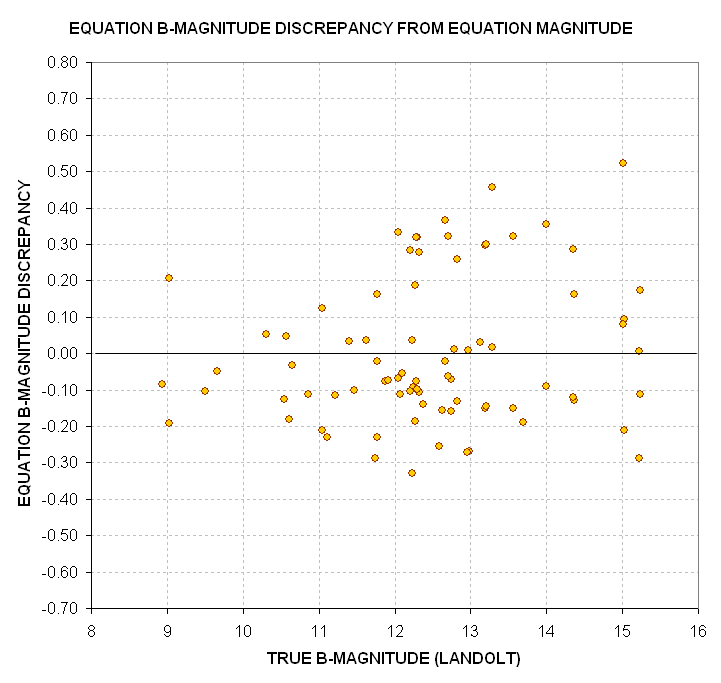
Figure 15. Discrepancies of simple "Equation B-magnitude" versus
True B-magnitude for 80 Landolt standard stars.
The next question we naturally think of asking is "Are these errors correlated
with air mass and star color." We also should ask if there's a statistically
significant correlation with the product "air mass times star color" since
a str's apparent color (entering the telescope aperture is affected by total
extinction). A multiple regression analysis should show whether there is
a signitificant correlation with any of these three independent variables.
The answer is "yes, the errors are correlated with all three independent variables."
The resultant discrepancies are much better "behaved" than those in the previous
figure which ignored these three new independent variables, as the following
graph shows.
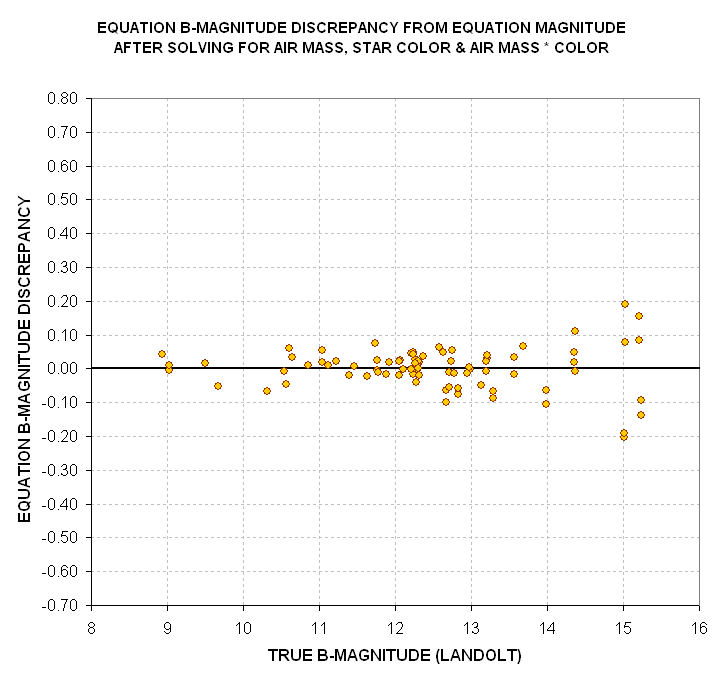
Figure 16. Discrepancies of "Equation B-magnitude" versus true
B-magnitude for 80 Landolt standard stars after solution that uses the three
independent variables: air mass, star color and "air mass times star
color."
The coefficients are +0.229 +/- 0.010 [magnitude per air mass], +0.090
+/- 0.051 [magnitude per B-V mag], and +0.063 +/- 0.027 [magnitude/air mass
times B-V mag]. All three correlation coefficients are statistically significant.
When these correlations are taken into account the simple equation becomes:
Notice that this equation uses 0.64 for a reference B-V star color; this
is the median B-V value for the 1256 Landolt stars in my data base. It will
be convenient to use (B-V)-0.64 as an indepenent variable in order to simplify
analyses for stars with unknown B-V colors (as will be apparent below). Also
notice that the LOG term has "10" in the numerator. This refers to the fact
that the measurements were made with an exposure time of 10 seconds. The
reciprocal of the LOG term is the ratio "Ib/10" and this ratio is merely the
rate of intensity counts per second, which should be the same for all exposure
times (neglecting stochastics).
In this plot the faint stars exhibit a larger scatter than the bright ones,
which is to be expected from SNR (signal-to-noise ratio) considerations.
Using all terms and coefficients derived for this B-band data leads to
an improved "Equation B-magnitude" as shown in the next figure.
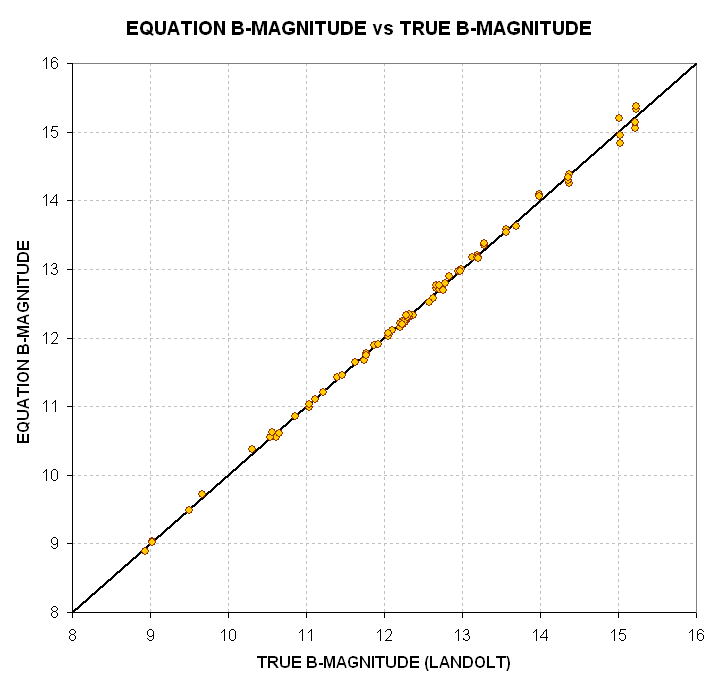
Figure 17. Equation-based B-magnitude (given in text, below)
versus true B-magnitude for 80 Landolt stars. The RMS scatter
for stars brighter than 15th magnitude is 0.043 magnitude.
This figure is to be compared with Fig. 14, which does not contain extinction
or star color terms. Clearly, the extinction and star color are important
independent variables for the task of inferring B-magnitude from measured
intensity. The final equation used for this data set is given below:
Equation B-magnitude = Cb1 + Cb2 * (2.5 * LOG(G/INTb)) + Cb3 * m + Cb4
* ((B-V) - 0.64) + Cb5 * m * ((B-V) - 0.64), where
Eqn 4
Cb1 = 19.31
[mag]
related to telescope aperture, filter width & transmission,
dirtiness of optics (including dew formation), signal aperture size,
Cb2 = 1.00
empirical multiplication factor (related
to non-linearity of CCD A/D converter),
Cb3 = -0.228
[mag/air mass] extinction for B-filter for the specific
atmospheric conditions of the observing site and date,
Cb4 = +0.097
related to observing system's color
response (i.e., the old CCD transformation equation coefficients),
Cb5 = +0.06
related to product of star color and air mass,
G = exposure time
(integration gate time), seconds
INTb = intensity
using V-filter (integrated excess counts within signal aperture that exceed
expected counts level based on average counts within sky reference annulus),
and
m = air mass,
with a residual RMS of
0.043 magnitude (for the 80 standard stars brighter than magnitude 15, air
mass range = 1.19 to 3.04).
Notice that Cb2 isn't necessary because it's 1.00; it is included for the
occassion when stars are included in the analysis that are so bright that
they begin to saturate the A/D converter in the CCD camera causing non-linearities
that affect only the brightest stars.
A similar analysis performed for the V-filter data yields the following.
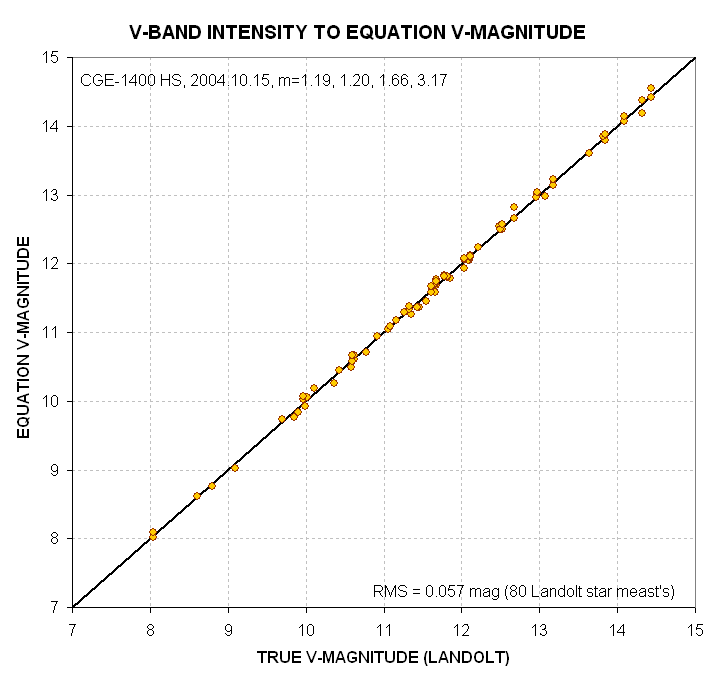
Figure 18. Equation-based V-magnitude versus true V-magnitude
for 80 Landolt stars.
Predicted V-magnitude can be expressed using the following equation:
Equation V-magnitude
= Cv1 + Cv2 * 2.5 * LOG(G/INTv) +Cv3 * m + Cv4 * ((B-V) - 0.64) + Cv5 * m
* ((B-V) - 0.64),
Eqn 5
Cv1 = 19.68
[mag]
related to telescope aperture, filter width & transmission, dirtiness
of optics (including dew formation), signal aperture size,
Cv2 = 1.00
empirical multiplication factor (related to non-linearity
of CCD A/D converter),
Cv3 = -0.147
[mag/air mass] extinction for V-filter for the specific atmospheric
conditions of the observing site and date,
Cv4 = -0.145
related to observing system's
color response (i.e., the old CCD transformation equation coefficients),
Cv5 = +0.06
related to product of star color and
air mass,
G = exposure time
(integration gate time), seconds
INTv = intensity
using V-filter (integrated excess counts within signal aperture that exceed
expected counts level based on average counts within sky reference annulus),
with a residual RMS of 0.057
magnitude (for 79 stars and air mass range of 1.19 to 3.17)
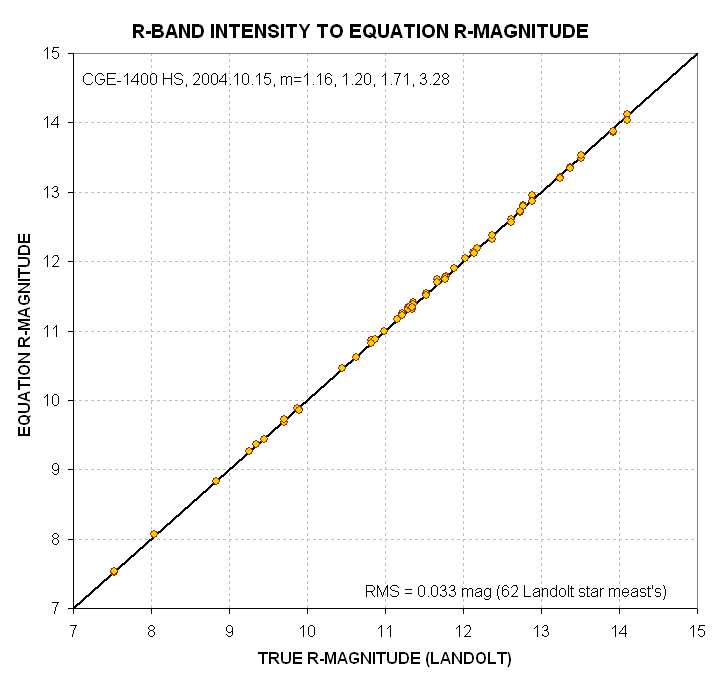
Figure 19. Equation-based R-magnitude versus true R-magnitude
for 62 Landolt stars.
The R-magnitude prediction equation is:
Equation R-magnitude
= Cr1 + Cr2 * 2.5 * LOG(G/INTr) +Cr3 * m + Cr4 * ((B-V) - 0.64) + Cr5 * m
* ((B-V) - 0.64),
Eqn 6
Cr1 = 19.83
[mag]
related to telescope aperture, filter width & transmission, dirtiness
of optics (including dew formation), signal aperture size,
Cr2 = 1.00
empirical multiplication factor (related to non-linearity
of CCD A/D converter),
Cr3 = -0.100
[mag/air mass] extinction for R-filter for the specific atmospheric
conditions of the observing site and date,
Cr4 = -0.110
related to observing system's
color response (i.e., the old CCD transformation equation coefficients),
Cr5 = +0.02
related to product of star color and air mass,
G = exposure time
(integration gate time), seconds
INTr = intensity
using R-filter (integrated excess counts within signal aperture that exceed
expected counts level based on average counts within sky reference annulus),
with a residual RMS of 0.033
magnitude (for 62 stars and air mass range 1.16 to 3.28)
Incidentally, it should be mentioned that unfiltered intensity measurements
can be used to infer V-magnitude. Here's a graph showing how well that can
work.
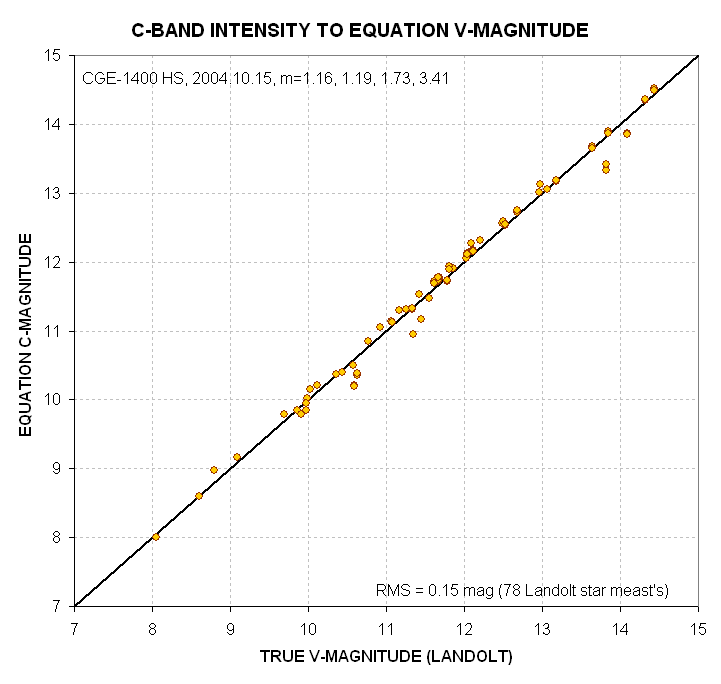
Figure 20. Equation-based V magnitude from unfiltered intensity
measurements, leading to what I'm calling C-magnitude.
The equation for C-magnitude (estimated V-magnitude from unfiltered intensity
measurements) is:
Equation C-magnitude
= Cu1 + Cu2 * 2.5 * LOG(G/INTu) +Cu3 * m ,
Eqn 7
Cu1 = 21.37
[mag]
related to CCD temperature, exposure time, signal aperture size,
telescope aperture, filter width & transmission,
Cu2 = 1.00
empirical multiplication factor (related to non-linearity
of CCD A/D converter),
Cu3 = -0.100
[mag/air mass] extinction for clear filter (unfiltered) for
the specific atmospheric conditions of the observing site and date,
G = exposure time
(integration gate time), seconds
INTu = intensity
using no filter (or "clear" filter),
with a residual RMS of 0.15
magnitude (for 78 stars and air mass range 1.16 to 3.41)
I am surprised that the attempt to infer a V magnitude using unfiltered
intensities, which I'm calling C-magnitude, works as well as this analysis
of 78 Landolt stars implies that it can. Almost all of the 0.15 magnitude
RMS can be attributed to not knowing the B-V star color (if that information
is allowed to be used the RMS becomes 0.054 magnitude). The typical situation
for trying to infer V-magnitude from unfiltered measurements is one in which
no B- or V-filter observations are available, so the 0.15 magnitude RMS performance
is the relevant performance number.
This site opened: 2012.07.09. Last Update: 2012.07.10