In order to conduct astrometry or photometry on faint asteroids it is necessary to perform image stacking, using either the median combine or average method. Asteroid motion requires that the stacking be performed using an alignment dot that "tracks" the asteroid's motion and is offset with respect to some arbitrarily chosen reference star. When there are few background stars near the asteroid it is not necessary to include "image subtraction." This web page describes image stacking when "image subtraction" is not needed. 

When observing fast-moving asteroids exposure times have to be kept short to avoid smearing of the asteroid's image. For faint asteroids this means they may be too faint in each image to be used for aligning images when stacking many images to achieve higher SNR. If the asteroid's rate of motion is known, only approximately, the user may add alignment dots to each image with offsets from a reference star, and these dots can be treated as an alignment star during the stacking process. When this is done using the median combine stacking tool, the asteroid's SNR improves while the background stars fade. With a sufficiently long observing interval the stars can be made to essentially disappear without affecting the asteroid's brightness.

Whereas the background stars can be remmoved using an "image subtraction" analysis procedure, which can be applied to each individual image, there are so many steps that must be followed in image subtraction that it is impractical for most observers. The asteroid alignment dot stacking described on this web page is much simpler, and in most cases it achieves almost as good a result, so I present it as an alternative solution for dealing with faint, fast-moving asteroids.

Rate of Motion

Assume that an ephemeris is available for the asteroid of interest, and it lists RA/Dec at hourly intervals during the night of observations.

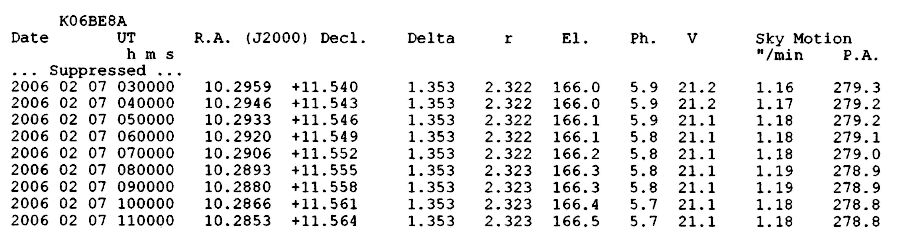
Figure 1. Ephemeris for a fast-moving faint asteroid. The RA & Dec positions are given in hours and fractions and degrees and fractions.

Notice that a negative sign has been added to the above equations. Using the values for our example,

    RA rate  = - (-1.17)  * 60 / 1.58  = +44.4 [pixel / hour]
    Dec rate = - (+0.18) * 60 / 1.58  =    -6.8 [pixel / hour]

This is the information we'll need for adding asteroid alignment dots to each image.

For the alternative method of determining asteroid rates of motion click here.

Star a spreadsheet for the observing session. Create cells for the RA and Dec motion rates.

Record the x,y location of the chosen reference star in a reduction log, and enter these values into XLS (whenever I use the term XLS it is meant to refer to the spreadsheet). Use one row per image, and record the start time for the image and the x,y coordinates for the reference star.

Here's a sample spreadsheet.

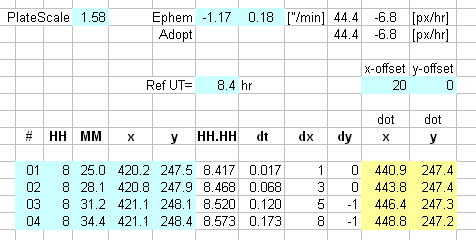
Figure 2. Spreadsheet showing 4 rows for image information (bottom) and rate of motion information (top). The light blue cells are for user entry, and the yellow cells are spreadsheet calculations to be used in positioning an alignment dot.

In this example spreadsheet the user enters 1.58 for PlateScale and -1.17 and +0.18 for the rates of motion [" / min]. The spreadsheet calculates the pixel / hour values. The user enters, for each image, the image file number, the start time in hours and minutes (including fraction of a minute, etimated), the x,y coordinates for the reference star. The user enters an arbitrary reference UT time, chosen here to be 8.4 hours, close to the first image's start time. The user also chooses x and y offset values that will place the alignment dot away from the reference star. The spreadhseet calculates the alignment dot x,y location using the user input data. The equation is for the alignment dot location is:

    Xdot = Xrefstar + (t - tref ) * X_MotionRate [px/hr] + Xoffset
    Ydot = Yrefstar + (t - tref ) * Y_MotionRate [px/hr] + Yoffset

The user then goes to the iamge and places a white dot at the specificed x,y location. using MaxIm DL, which everybody should, this done using the Pixel Edit tool. Specify the new pixel value to be large, such as 65,000, and go to the x,y location and replace the pixel's value by this new value, making it look white and appear like a sharp star.

Median Combining Images Using Alignment Dot

Since we will want to do astrometry on the image produced by stacking images we must do a PinPoint solution on the first image in the series.

Then start a Median COmbine, MC, by first loading the image with thte PnPoint astrometry solution into the window of images to be combined. Select "Manual 1 Star - shift only" for alignment, and when the combine images appear click on the alignment dots. The MC'd image will retain the astrometry solution so if the asteroid can be seen it should be possible to determine its coordinates. Here's an example of a 4-image median combine.

Figure 3. Example of stacking 4 images using an asteroid alignment dot (upper-left) and showing the 21.1 magnitude asteroid (photometry circles) with SNR = 4.8.

In this median combined image the stars have elongated shapes while the asteroid is circular. The photometry apertures have been chosen in this presentation to maximize SNR. Notice that the signal aperture is small, yet fully encloses the asteroid brightened pixels, and the sky background annulus is free of interfering stars. The asteroid in this image has SNR = 4.8, whereas in the four images used to create it the SNR was ~2.2 and in some cases it could not be seen.

If it is clear that no stars are near the asteroid the image combining can make use of "averaging" instead of "median combining." This will add about 15% to the SNR.

Image Subtraction

The case illustrated is fortunate in not having stars near the asteroid. If such stars were present then this procedure would not work, and "image subtraction" would be required.

The user should be aware of this limitation. Interfering stars should always be a concern, and if they are not present then image subtraction does nothave to be used. If it is needed, however, there's a description at Image Subtraction Tutorial.

APPENDICES

Alternative Asteroid Rate of Motion Method

    RA rate [deg/hour] = (10.2853 - 10.2959) / 8

    Dec rate [deg/hour] = (11.564 - 11.540 ) / 8

Using a hand calculator, we have

    RA rate = -0.001325 [RA hours / hour]

    Dec rate = +0.0030 [Dec deg / hour]

This site opened:  February 9, 2006.  Last Update:  March 30, 2006