Links internal to this web page:
    Introduction
    2006 & 2007 Light Curves
    2005 My First Observation  

Introduction

When someone names an asteroid for you it's incumbent upon the recipient to try to determine as much about that asteroid as possible. Since I like observing challenges this asteroid's faintness, at ~18th magnitude, typically, was an added incentive for me to hone my observing and analysis skills. This web page describes what a dedicated amateur can learn about a faint asteroid if the motivation exists.

Asteroid "86279 Brucegary" was discovered in 1999 by Jeff Medkeff and David Healy using the Junk Bond Observatory (in Sierra Vista, AZ). It's orbital elements and standard (1 a.u.) brightness are:

    a = 1.931865 a.u. (semi-major axis)
    i = 21.9853 degrees (inclination)
    e = 0.0679895 (eccentricity)
    H = 15.9 (16.2 my suggested revision)

Based on the two orbital parameters a and i this asteroid can be identified as a member of the "Hungaria" family. The smallness of this asteroid family is shown in the following scatter diagram of 10,592 asteroids observed by SDSS (reported by Ivezic et al, 2002).

 

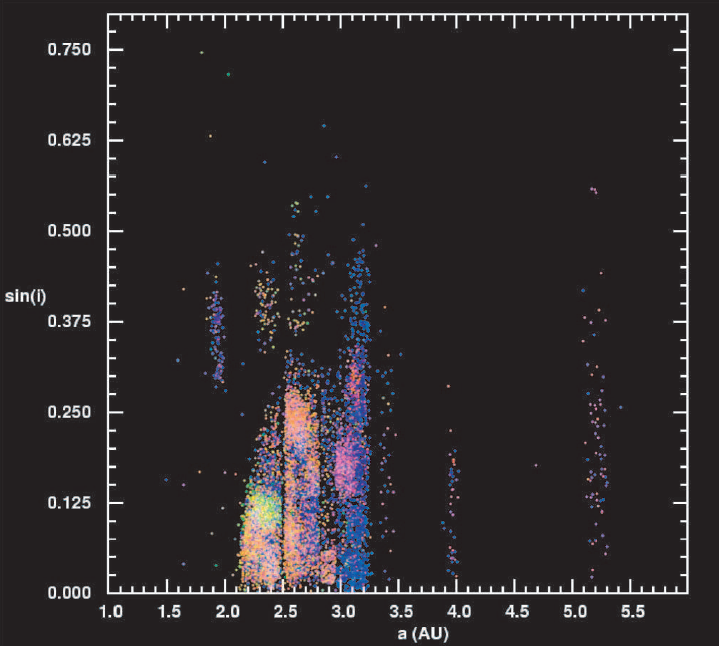
Figure 1. Scatter diagram of "sine(inclination" versus semi-major axis for 10,592 asteroids observed with the SDSS telescope and reported by Ivezic et al, 2002. Each asteroid dot is colored to represent its SDSS g, r, i, z colors. Asteroid 86279 has sine(inclination) = 0.374 and semi-major axis = 1.93 a.u., which places it within the upper-left group in this diagram (close and highly inclined). (Note: Mars orbits at 1.52 a.u., and at its farthest is at 1.68 a.u.)

As of mid-2004 there were 3375 Hungaria asteroids tabulated, which represented 1.6% of all 214,044 categorized asteroids (Faure, 2004).

What is the asteroid's size? We need to estimate the asteroid's albedo in order to convert its brightness to a diameter. The next plot is a summary of measured albedos versus semi-major axis.



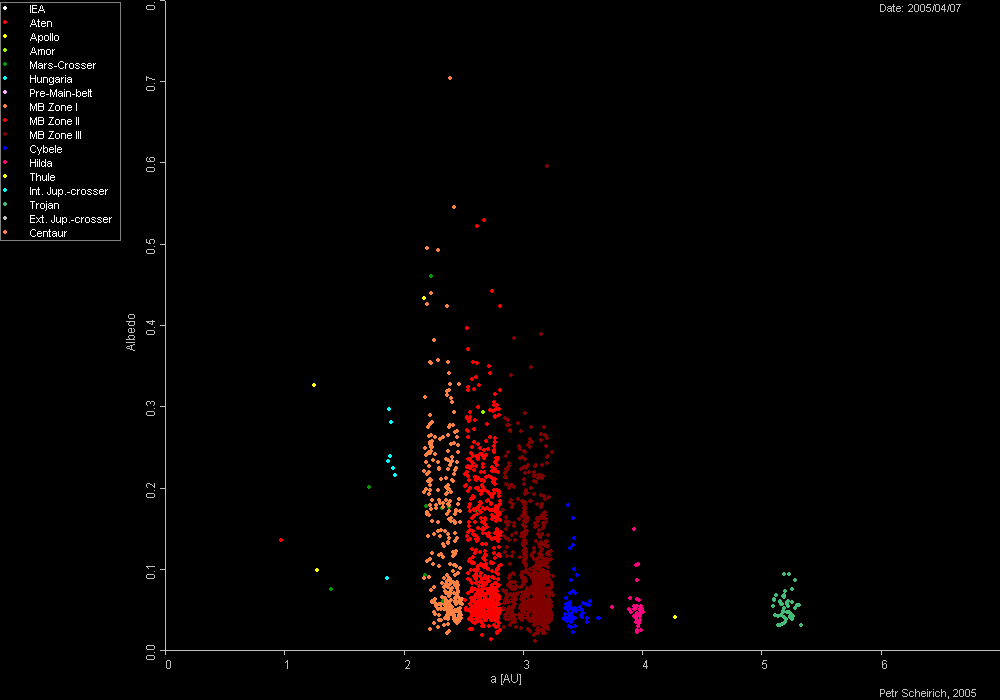
Figure 2. Albedo versus semi-major axis (Plot created by Piotr Deuar, appearing in Wikipedia).

In this figure there are 7 Hungaria asteroids, and their median albedo is 23% (range is 9 to 30%). As shown below, the asteroid's standardized brightness is V-mag = 15.76 (estimated SE = 0.05 mag). This corresponds to a diameter of 1.9 km (range is 1.7 to 3.1 km).



2006 and 2007 Light Curve Observations

Here's a chi-squared "solution" for the rotation light curve shape and period based on adjusted observation dates: 20060128, 20060131, 20071008, 20071011, 20071101 and 20071107 (UT).



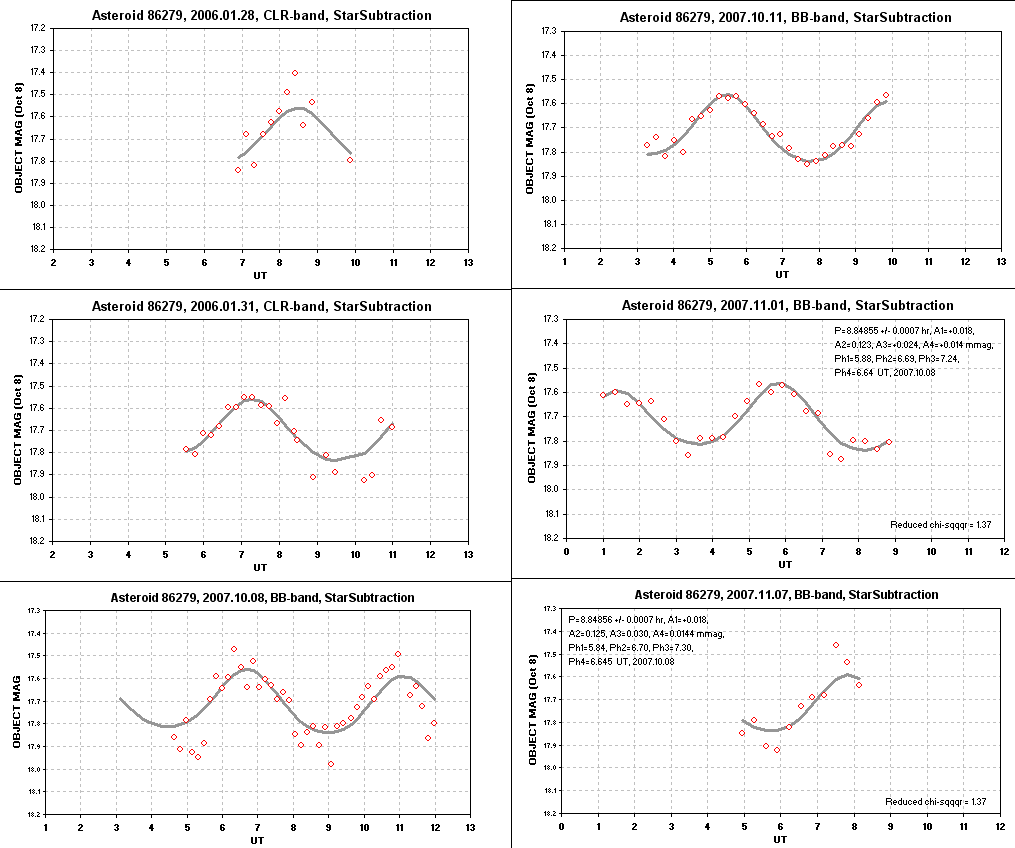
The "adjustments" consist of two things: 1) magnitude offsets to compensate for distance and sun-asteroid-earth geometry (from an ephemeris), and 2) time shifts caused by the same sun-asteroid-earth angle and hypothetical rotation period. This second adjustment causes a similar rotational aspect to be observed either earlier than or later than an average periodic interval depending on whether the asteroid is before or after opposition. If the rotational vector pointed at the ecliptic north pole, for example, before opposition a given aspect would be viewed before a uniformly spaced schedule and after opposition it would be later. This means the asteroid's rotation direction, prograde versus retrograde, can be determined. For the above solution only the prograde hypothesis produced a good solution.

Based on these observations it appears that the asteroid's rotation period is 8.84856 ± 0.00003 hours. The average peak-to-peak brightness variation is 0.26 magnitude, implying that the asteroid's projected solid angle varied by 27% (i.e., the largest area projection was ~27% greater than the smallest). This assumes a uniform albedo and similar shape for all sides. However, since the two minima are different the ends must have different shapse. The peaks are about the same, so the opposite sides probably have the same projected area and albedo.

The measured magnitude offsets from ephemeris values predicted a magnitude average -0.14 magnitude. In other words the average V-magnitude is brighter than the ephemeris values by ~14%. This requires that the ephemeris H value be changed from 15.9 to 15.76 (assuming  G = 0.15 is correct and my all-sky calibration is correct).

Image Subtraction Analysis

[Note: this section describes an image processing procedure that removes a background star field image from individual asteroid images that produces a residual image showing the asteroid at 100% of its true value and stars at ~1% of their original value. Since I wrote this I have made small improvements in analysis procedure, but the basic concept is the same. Later, when I settle on a final procedure, I'll update this section.]

An image subtraction technique was used to process observations made 2006.01.28 UT with my 14-inch Celestron. Downslope winds cause seeing to vary from bad to poor, with FWHM ranging between 4.5 to 6.0 "arc (for 4-minute exposures).

Let's begin with an image of the star field showing the path of the asteroid during the 3-hour observing period.



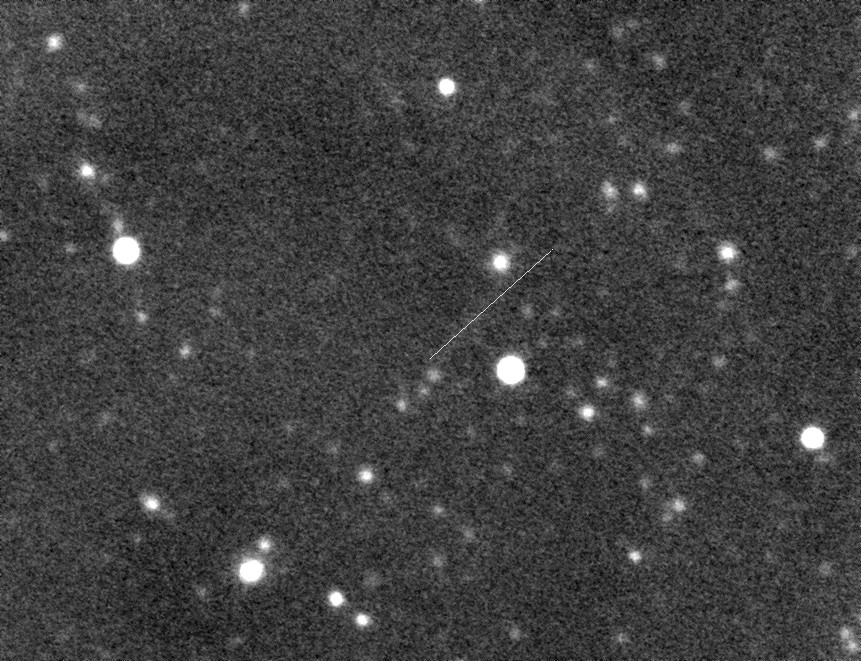
Figure 2. Path of asteroid during the 3-hour observing period of 2006.01.28. At the beginning (lower-left) the asteroid is just north of a 19.1 magnitude star. The asteroid does not appear in this image because it is a median combine of 21 images during which the astreroid's location changed. The faintest stars have CV magnitudes of 22.2 (SNR=3). The brightest star (saturated in this 8-bit image, but not saturated in the 16-bit FITS image) has CV = 14.59 with FWHM = 6.0 "arc. The FOV is 8.6 x 6.6 'arc (cropped from the original 15 x 10 'arc image). North up, east left. [Total exposure = 84 minutes.]

The next image is a median combine of the first 3 images (cropped the same as the previous image).



Figure 3. Median combine of first 3 images, showing asteroid (cicled) at the beginning of its path for the night.

The asteroid is close to a 19.1 magnitude star, located to its south within the sky reference annulus. Any attempt to measure the asteroid's brightness would be affected by the nearby star. This is when "image subtraction" is useful.



Figure 4. Same star field after image subtraction, showing the asteroid without interference from nearby stars.

Let's show the before and after versions of the previous two images for a smaller FOV.



Figure 5. Before and after image subtraction (for a smaller FOV) for the first 3-image set.

Notice that the 19th magnitude star to the asteroid's south is completely removed after image subtraction. Only the 14.6 magnitude star is present as a ghost feature with an approximate brightness comparable to the 18.7 magnitude asteroid. Thus, the image subtraction processing achieved a star subtraction of about 4 magnitudes (40-fold reduction).

If you want to learn more about the image processing procedure used on this data go to IS for 6128.

Animation of Asteroid Motion



Figure 6. Animation of asteroid's 3-hour motion, using cropped versions of the image subtraction images.

Notice that in this animation there is no hint of other stars besides the ghost of the bright 14.6 magnitude star. This suggests that the image subtraction process did what it was suppsoed to do.

Fuzzy Animation

Here's an animation from "smoothed" versions of the same images (only 10 frames).

 

Figure 7. Same animation but with smoothing applied.

2005 January Observation

The discovery of "86279 Brucegary" was made 1999.10.17 by Jeff Medkeff and Dave Healy. They used Dave's Junk Bond Observatory 20-inch Ritchey-Chritien (loaner) telescope in Sierra Vista, AZ (3 miles from my place).

The asteroid has the following known properties:

    Semi-major axis = 1.932 a.u.
    Eccentricity = 0.068
    Inclination = 21.8 degrees (unusually large)
    Absolute magnitude = 15.9 (my suggested revision calls for 15.8)

The brightness implies a diameter of ~3.0 km (based on the H value and an albedo of 0.15).

Of course, I had to take a "picture" of it as soon as I learned about the official naming.
 
 

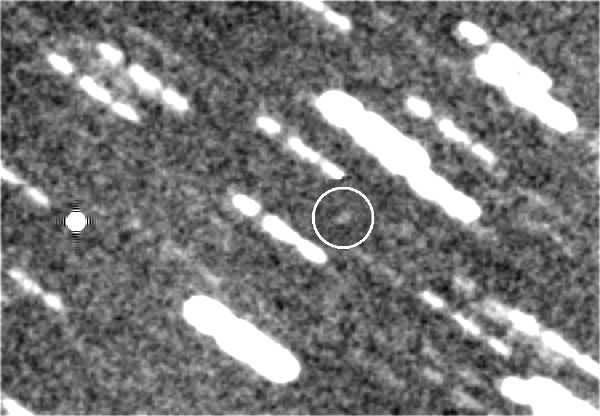
 Figure 8. Stack of 48 one-minute exposures, using the predicted position of the asteroid for alignment. Unfiltered brightness corresponds to V-mag = 20.6 +/- 0.13 (SNR = 8). [Celestron 14-inch, prime focus, f/1.86, SBIG ST-8XE; 2005.01.29; Hereford, AZ]
 
Measuring the brightnessof a stationary object with a V-magnitude of 20.6 is easy for amateurs, but a moving object of the same brightness is more difficult. This asteroid was moving at the rate of 3.8 "arc/minute, which meant that exposures could not exceed ~1 minute. The asteroid's motion was known, so I added an "artificial star" to each image that was carefully offset from a nearby bright star by an amount that corresponded to the asteroid's motion. I then used this artificial star for alignment of groups of 4 images while performing a median combine. Since there were 48 one-minute images, this led to a set of 12 median combined images, each of which was cleansed of any artifact blemishes (such as cosmic ray features). These 12 images were averaged, again using the artificial star for alignment. Voila! At the predicted location there appeared a 20.6 magnitude object which I assume is the asteroid. It was located 1.6 pixel to the east and 0.1 pixel to the south of the predicted location. 

Nearby Tycho stars were used to establish the magnitude scale, which I estimate allowed me to establish a magnitude scale accurate to 0.07 mag, SE. The ephemeris predicted a magnitude on the observing date of 20.3, so based on my measured magnitude I am suggesting that the asteroid is 0.3 magnitude fainter than assumed by the ephemeris program. In other words, I am suggesting that H = 16.2 (instead of 15.9). Of course, there are two other alternative reconciliations of this brightness difference. The asteroid rotates, and I observed it near minimum, and the assumed opposition effect differs from the adopted value describing the fall of of brightness with increasing sun-object-observer angle (G = 0.15). My observation was made close to the time when the asteroid was on the opposite side of the sun from the Earth. It was ~2.9 a.u. from Earth, whereas at opposition it will be ~1.3 a.u. away, and will be at 18.8 magnitude (at declination +42 degreese).


References

Faure, Gerard, http://www.astrosurf.com/aude/map/us/AstFamilies2004-05-20.htm

Ivezic, Z., Lupton, R. H., Juric, M., Tabachnik, S., Quinn, T., Gunn, J., Knapp, G. R., Rockosi, C. M., Brinkmann, J., "Color Confirmation of Asteroid Families," A. J., 124, 2943-2948, 2002 November.

Return to AstroPhotos