Figure 2. SED for a star with Landolt and SDSS magnitudes (as well as 2MASS mag's).
Converting Magnitudes to SED
(Spectral Energy Distribution)
Bruce L. Gary, Last Updated
2014.10.18
Suppose you want to know a star's
"spectral energy distribution" (SED). If it's brighter than
~ 16th magnitude it will have good quality mag's for bands
BVg'r'i'JHKs, thanks to the AAVSO's APASS project (AAVSO
Photometric All-Sky Survey)
and the 2MASS project (2-Micron All-Sky Survey). There's an
easy conversion of these magnitudes to star flux at the
bandpass equivalent wavelength.
V-mag Example
This section may look complicated, but that's just because we're
going through the logic of what needs to be done. In the next
section you'll see how easy it really is.
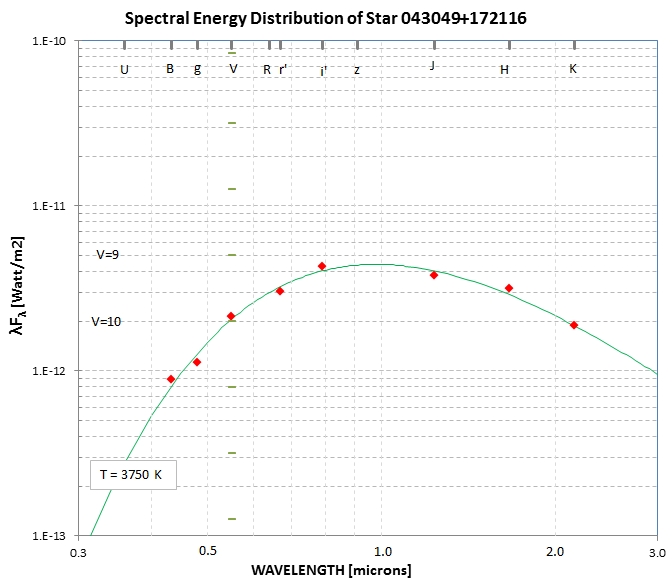
Consider the star at 043049+172116 (J2000), with V-mag = 9.978.
It is fainter than a zero magnitude star by the factor
10^(-0.4*9.978) = 1.020e-5. Since a zero mag star at V band has a
flux of 3836 Janskys (Jy), our star of interest has a flux of
0.391 [Jy]. Since a Jy is defined to have units of 1e-23
[erg/s/cm2/Hz], the star's flux = 3.91e-24 [erg/s/cm2/Hz]. We
don't care about Jy, because we're not a radio astronomer; we want
flux in units of either [erg/s/cm2/micron] or [watts/m2/micron] or
[watts/m2]. Let's go through the steps for each.
Note: Just to be clear, when I write [erg/s/cm2/micron] I mean
[erg / (s · cm2 · micron)]. Also, from now on I'm going
to abbreviate the word "flux" with F, and wavelength will be given
as λ.
If we multiply F [Jy] by c/λ2 we'll get F
[erg/s/cm2/cm], provided we use c = 2.997924e10 [cm/s].
Since this is flux per unit wavelength interval let's call it Fλ.
CCD counts are proportional to the number of photo-electrons
counted, and longer wavelength photons have less energy than
shorter wavelength ones. Therefore there's a good reason to create
a version of F that is proportional to photon flux. This is
achieved simply by multiplying Fλ [erg/s/cm2/cm] by λ
[cm]. This new flux is called λFλ[erg/s/cm2]. If
you prefer λFλ[watts/m2], as I
do, then multiply by 1e-3. Returning to the example,
above, with F = 3.91e-24 [erg/s/Hz], and λ = 550 [nm] = 5.50e-5 [cm], we can calculate
Fλ = 3.91e-24 [erg/s/Hz] * {2.998e10 /
(5.50e-5)^2} = 3.88e-5 [erg/s/cm2].
Also, λFλ
= 2.13e-12 [W/m2] = 2.13e-12
[watt/m2].
Generalizing the V-mag Example
Mathematically, all we did in the
previous example is: λFλ
[W/m2] = 11.50e-9 × (10-0.4 V) / λ [micron].
In other words, the general equation is a constant
(associated with the filter band in question) times a
magnitude ratio divided by wavelength in microns. To
simplify further, let's define a "SED Constant" that
includes the wavelength, so that:
λFλ [W/m2] = SED Constant × 10-0.4 Mag
which allows us
to present the following table listing the SED
Constant:
| Band |
Effective Wavelength [micron] |
Jansky Constant [erg/s/cm2/Hz] |
SED Constant [W/m2] |
| B |
0.433 |
4267 |
2.954E-8 |
| V |
0.550 |
3836 |
2.091E-8 |
| Rc |
0.640 |
3080 |
1.443E-8 |
| Ic |
0.790 |
2550 |
0.968E-8 |
| g' |
0.481 |
2.48E-8 |
|
| r' |
0.670 |
1.75E-8 |
|
| i' |
0.790 |
1.40E-8 |
|
| z' |
0.910 |
1.22E-8 |
|
| J |
1.235 |
1594 |
3.869E-9 |
| H |
1.662 |
1024 |
1.847E-9 |
| Ks |
2.159 |
667 |
0.926E-9 |
Table 1.
The last column is used to calculate star
flux according to the
equation λFλ
[W/m2]= SED Constant × 10-0.4 MAG, where MAG is star
magnitude. "Jansky Constant" is given merely
for anyone wanting to know the basis for
deriving the SED Constant. The g'r'i'z' SED
Constants are my empirical values.
Getting APASS & 2MASS Mag's
My favorite planetarium program for obtaining magnitudes is C2A (http://www.astrosurf.com/c2a/english/). This is a free program, and it supports the UCAC4 database if you have it on your computer. TheSky6 and TheSkyX also support UCAC4, but C2A is easier to use.Creating the SED
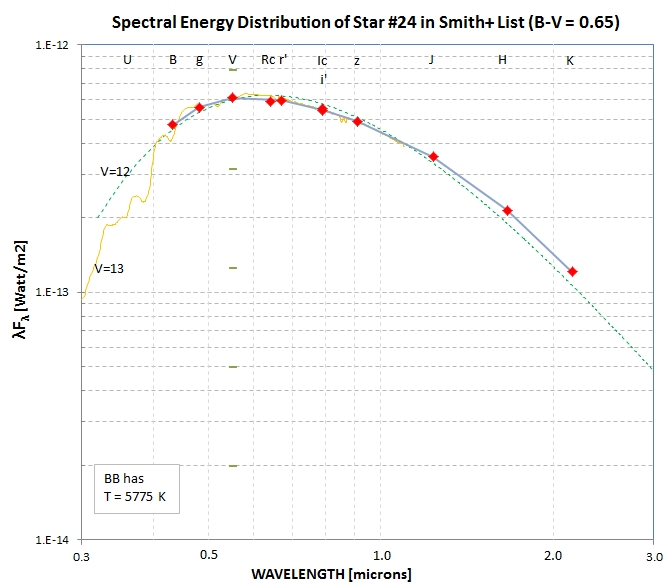
Here's an example of a SED for the star used in the above example.
When the star is fit well by a blackbody (BB) function it is a
simple matter of representing the star's flux at any desired
wavelength (within the wavelength range where the fit is good).
This is useful for creating a SED for target stars not in the
UCAC4 catalog, and especially for asteroids. For example, using a
spectrograph in an attempt to create an asteroid's SED the
procedure can be to 1) measure the spectrum for a nearby star, 2)
measure the spectrum for the asteroid, 3) create a SED for the
nearby star using BVg'r'i'JHK magnitudes (as demonstrated above),
4) use the BB fn to calculate a flux spectrum for the nearby star
at the resolution of the spectrograph, and 5) use the ratio of the
asteroid's measured spectrum to the nearby star's spectrum,
multiplied by the BB fn of the previous step, to arrive at the
asteroid's flux spectrum. If the goal is to determine the
asteroid's geometric albedo, for example, then the asteroid's flux
spectrum can be divided by the sun's known flux spectrum, etc. An
illustration of this, using a transmission grating (SA100) is
shown at this link: http://brucegary.net/Albedo/.
Another Example
The Landolt stars have excellent quality BVRcIc magnitudes, and
the Smith et al (2000) SDSS stars have excellent g'r'i'z'
magnitudes. The latter catalog is a subset of the former, so it
includes all of the above magnitudes. Here's an example for Star
#24 in my list of Smith et al stars.

Figure 2. SED for a star with Landolt and SDSS
magnitudes (as well as 2MASS mag's).
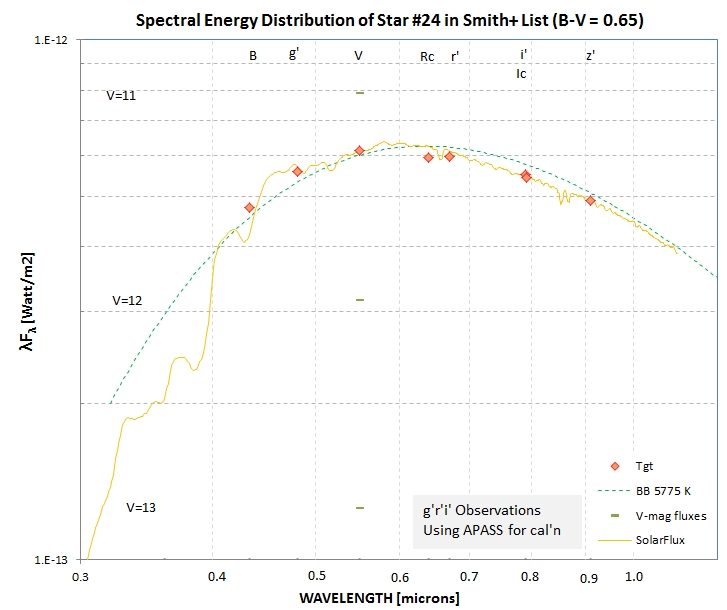
Figure 3. Same SED for the visible region.
BGary master list of web sites: http://brucegary.net/MASTER.html
____________________________________________________________________
This site was opened 2014.09.06. Nothing on this
web page is copyrighted. BGary web sites