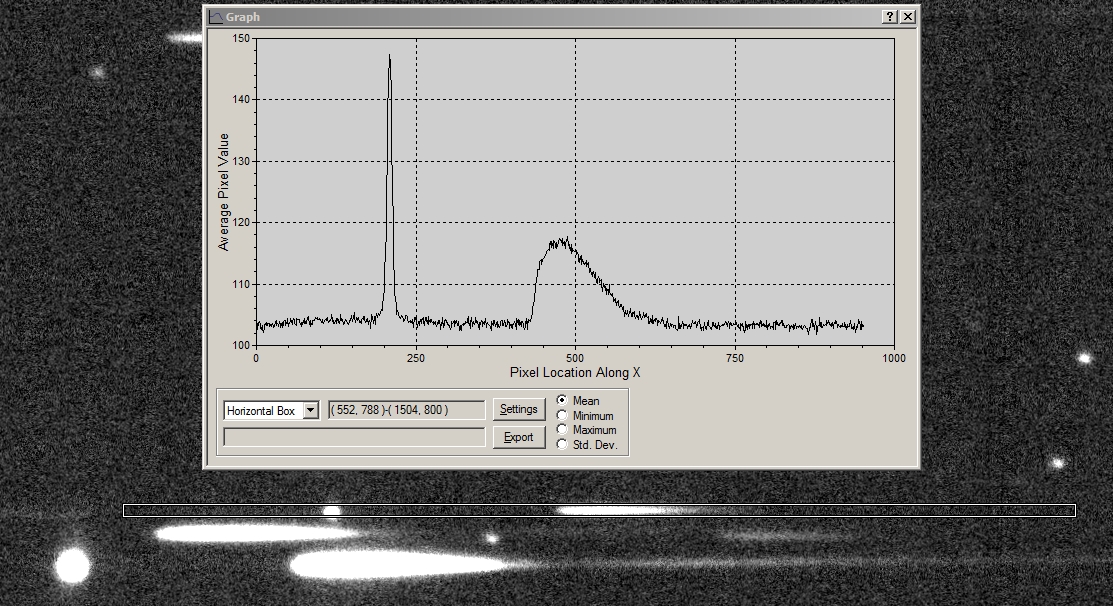
Figure 2. MaxIm DL's "Profile" tool captures the sum of counts within each column of a horizontal box for a long stretch of rows, that contain spectrum information. The horizontal box has a "vertical width" of 12 pixels.
Determining an Asteroid's
Albedo
Using the SA-100 Transmission Grating
Bruce L. Gary, Last Updated
2014.09.08
This web page demonstrates that using a SA-100 transmission grating with a 12.5-inch Schmidt-Cassegrain telescope is adequate for deriving the flux spectrum of stars (and asteroids) as faint V-mag = 14.0 (and probably fainter) for the wavelength interval 470 to 800 nm. For V-mag = 12 the longest useable wavelength is 900 nm, while brighter objects can provide useful flux spectra to ~ 1000 nm. Flux spectra can be processed to produce standard magnitudes BVg'r'i'z', and the necessary procedure for doing this is given. Two SA-100 calibration methods are compared: all-sky photometry using a well-calibrated standard star and differential photometry using another star in the same FOV. Both methods are feasible, but the best results are obtained using all-sky photometry. The only exception is when the atmosphere is very humid and spatial structure of line-of-sight water vapor is likely; for that situation calibration using a background star in the same FOV is preferred. This method requires the conversion of a star's magnitudes (BVg'r'i'JHK) to a Spectral Energy Distribution (SED), with a blackbody fit for use in the SA-100 calibration. Converting SA-100 flux spectra to geometric albedo is demonstrated for Vesta, 23 Thalia and Scythia.
The SA-100 transmission grating is
designed for use by amateurs for obtaining low resolution (1%) spectra
of stars, asteroids, planetary nebulae, etc. It costs $200
and screws into a typical 1 1/4-inch filter wheel. This web
page demonstrates how to use the SA-100 for determining as
asteroid's albedo. Geometric albedo can be determined if
sufficient brightness versus phase angle information is
available. The procedure to be described is novel, as far as
I know, for it employs a "differential photometry technique"
(instead of the more difficult all-sky photometry technique)
for calibration, which relies upon a SED (Spectral Energy
Distribution) for a nearby star in the CCD's FOV instead of
an already calibrated secondary standard star. I will
illustrate use of both calibration techniques on this web
page.
Links on This Web Page
Example 1:
Geometric albedo spectrum using background star for SA-100
calibration
Example 2:
All-sky calibration alternative, Vesta geometric albedo
spectrum using 59 Vir
Dangers
of all-sky calibration (due to water vapor inhomogenities)
Equation
for calculating geometric albedo
Example 3:
Faint asteroid (V=14.1) using all-sky calibration (51Peg);
all-sky and background star calibration methods compared
Converting
flux spectrum to standard magnitudes
Standard
filter band measurements; comparing magnitudes from
SA-100 with those using standard filters
Example #1: Geometric Albedo Spectrum Using Background Star for SA-100 Calibration
The following image was made with a Celestron CPC-100 (11-inch)
telescope and a SBIG ST-10XME CCD. A "clear with blue blocking"
was included in the optical path to reduce the 2nd order spectrum
from interfering with the long wavelength portion of the 1st order
spectrum (described later). The image is a median combine of 19
10-second exposures.

Below is a "profile" of the asteroid's spectrum.

Figure 2. MaxIm DL's "Profile" tool captures the sum of
counts within each column of a horizontal box for a long stretch
of rows, that contain spectrum information. The
horizontal box has a "vertical width" of 12 pixels.
The profile's spike is the zero-order (straight-through) image of
the star (~28% of total incident light). Plenty of baseline level
information is retained in this long profile, as well as some
2nd-order information. The exported CSV-file is loaded into a
spreadsheet that I've prepared for such data.
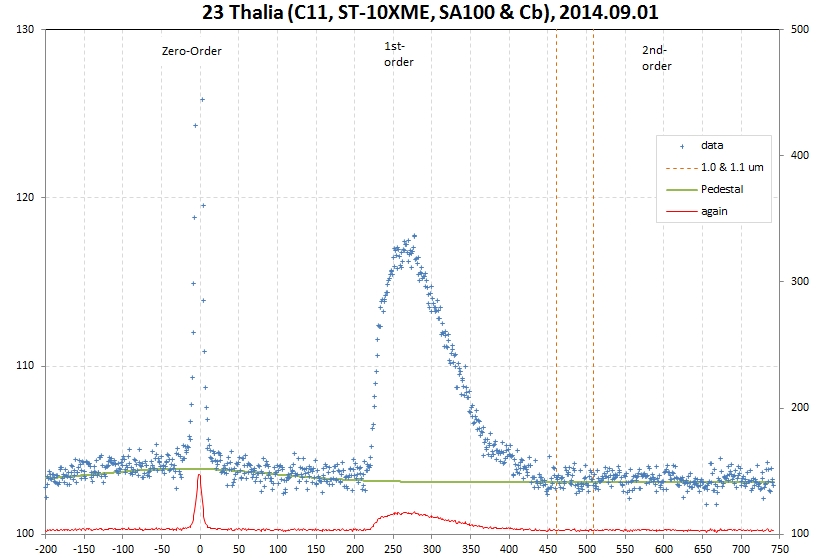
The above plot is total counts for each 12 pixel wide column
versus pixel distance from the 0th-order star-like image. From an
analysis of other stars I know the pixel-to-wavelength
conversion: λ
[nm] = 12
+ 2.140 * pixel location. The two vertical dashed lines represent
1000 and 1100 nm. For bright stars (or asteroids) there is
measurable flux out to ~ 1100 nm.
This profile by itself is essentially useless. We need to
calibrate it using a star with a known spectrum. That's what the
bright star in the lower-left corner (c.f., Fig. 1) will be used
for. This star has coordinates 04:30:49.0 +17:21:16, so I'll refer
to it as RefStar043049. It is ~2.02 magnitudes brighter than 23
Thalia (at the time of this image). Below is a profile of this
star, made in the same way as for the asteroid.
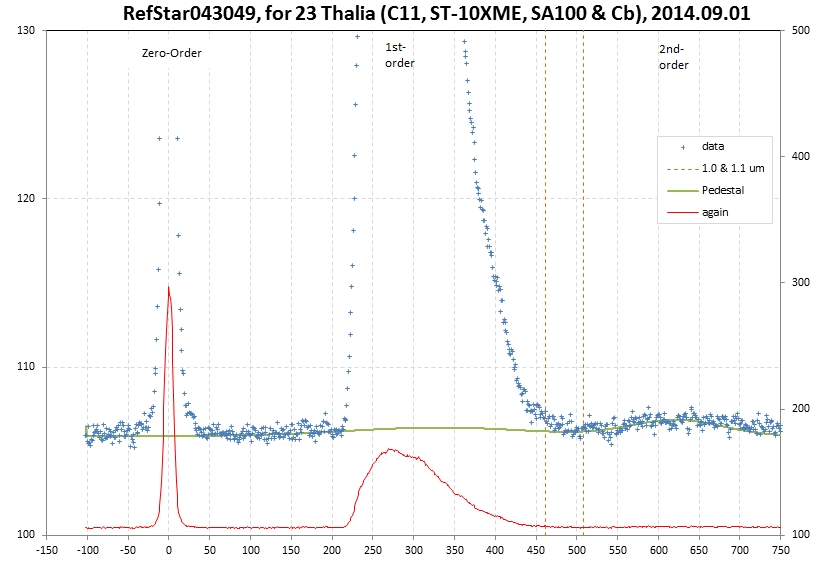
Now we need to know the flux spectrum of the reference star. A
detailed procedure for doing this is given at this web page:
http://brucegary.net/SED/.
Briefly, we enter magnitude values for the bands BVg'r'i'JHK in a
spreadsheet that converts each magnitude to a flux value. Here's
the reference star's flux spectrum with a blackbody fit:
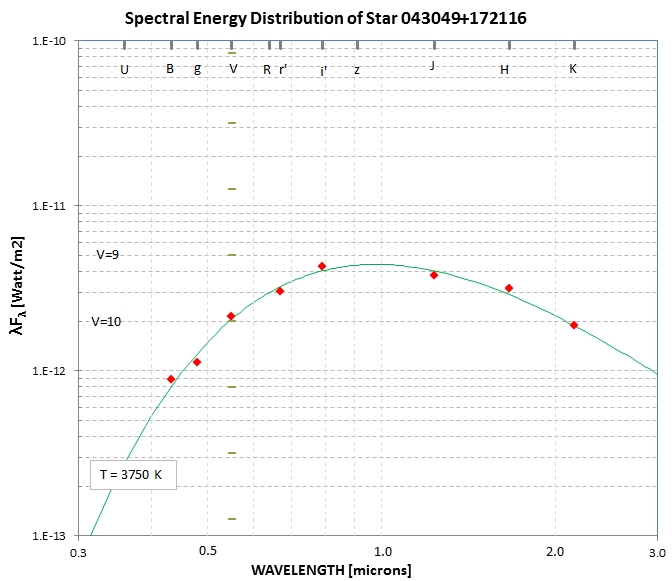
The plotted flux is a special version that is proportional to
photon flux, which is what CCD counts is proportional to.
In the spreadsheet a ratio is calculated for "23 Thalia Counts /
RefStar043049 Counts" vs. wavelength. This is multiplied by the
blackbody function that fits the flux spectrum of the reference
star. Notice that by representing the reference star's flux
spectrum by the blackbody fit it is possible to calculate flux
values at each of the wavelengths sampled by the SA-100. We arrive
at a flux spectrum for 23 Thalia, shown in the next figure.
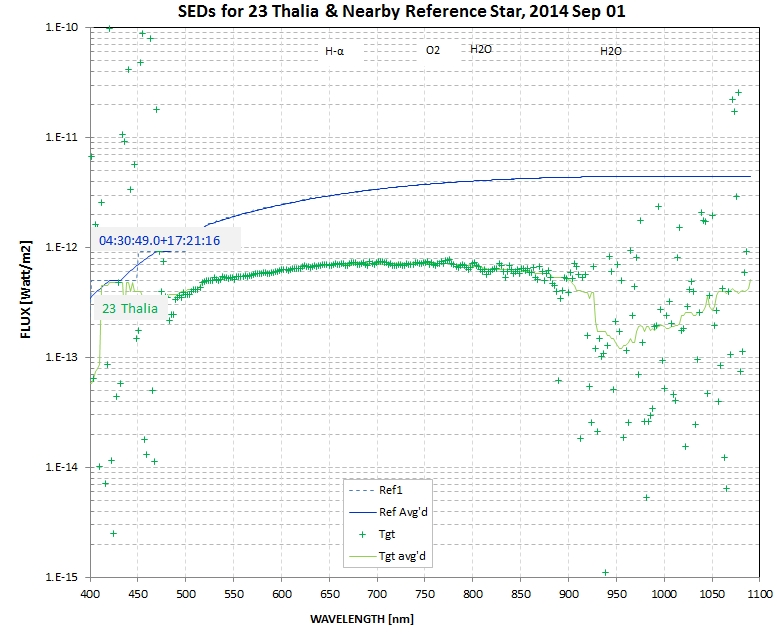
Notice that the 23 Thalia data is noisy at short and long
wavelengths, where SNR is low. The short wavelength region has low
SNR due to the use of a "clear with blue blocking filter," which
turns on at ~ 480 nm. At SNR at longer wavelengths is low for
several reasons: 1) the CCD's QE is low and decreasing steeply
with wavelength, 2) the telescope's corrector plate has a
transmission function that decreases steeply with wavelength, and
3) the asteroid's reflected sunlight is is decreasing with
wavelength.
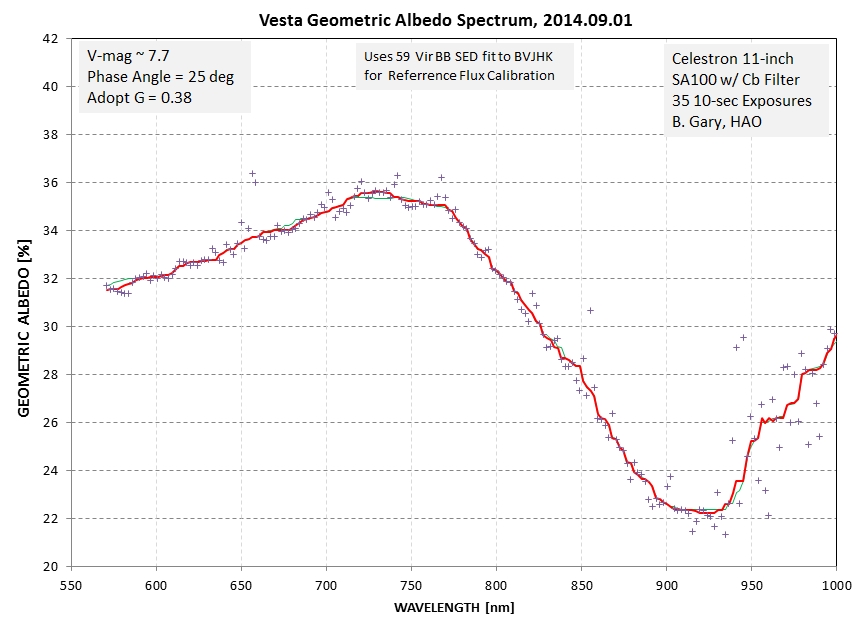
We now know the asteroid's flux spectrum, and since the sun's
flux spectrum is well known we can simply take their ratio to
obtain a shape for the asteroid's albedo. Here's the solar flux
spectrum.
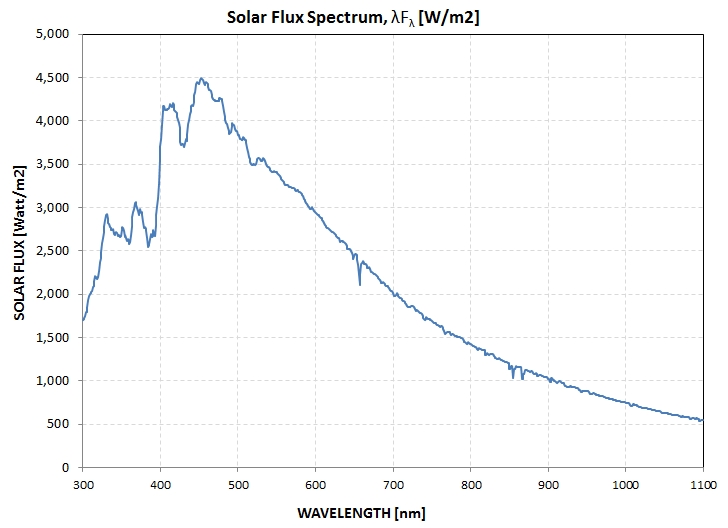
After dividing the asteroid's flux spectrum by the solar flux
spectrum we arrive at a shape for the asteroid's albedo, shown
below.
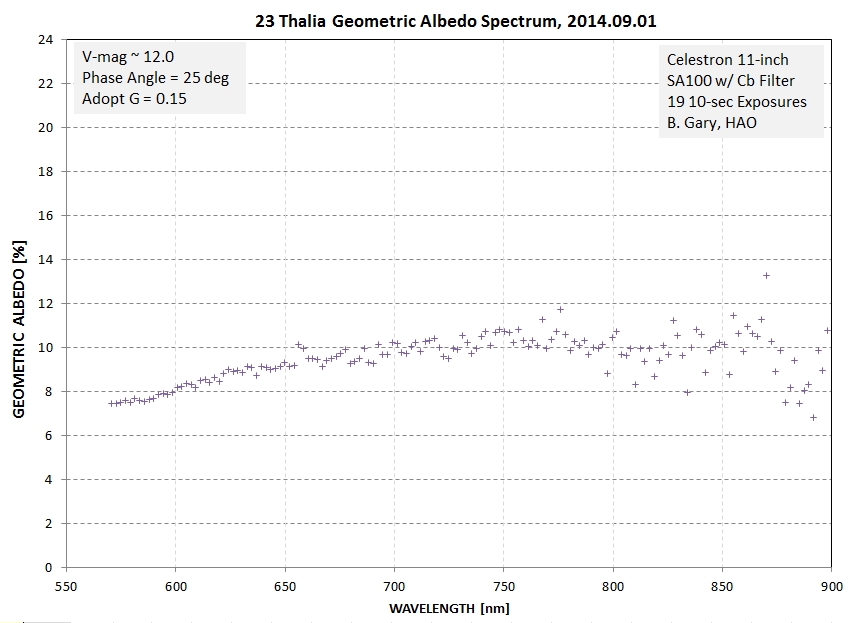
Here's an example that illustrates a shortcoming of using the
all-sky technique for establishing the spectrum of another star
during high water vapor burden conditions (varying between 3.7 cm
and 6.5 cm during 30 hours during previous & following
daytimes).
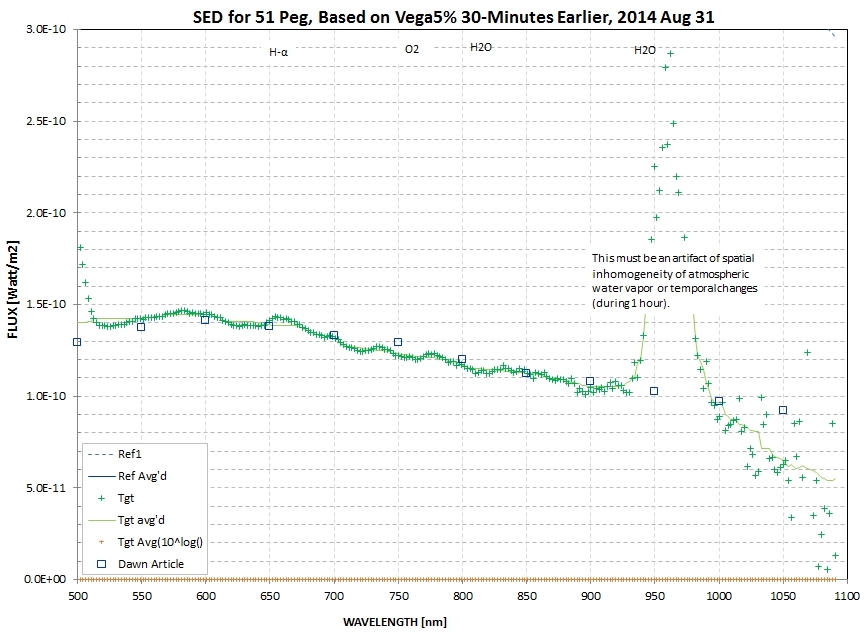
This comparison shows good agreement from ~ 520 nm to 925 nm; the
"artifact" at ~ 960 nm has the shape of the water vapor absorption
complex of lines, so it must be produced by a difference in the
water vapor for the two line-of-sights (Vega and 51 Peg, at same
air mass, but different parts of the sky). The loss of data
quality longward of ~ 1020 nm is due to small flux levels for the
Vega observations (1-second exposures, to avoid saturation at
short wavelengths, with a 5% mask).
This is why I prefer to use the "differential photometry"
technique for calibrating SA100 spectra, at least when water vapor
burden is high and potentially variable.
Calculating
Geometric Albedo
In case you're interested in calculating geometric albedo, here's
the equation.
Ag[%] = 100 × GeometryRatio × FluxRatio,
where GeometryRatio = ( r[a.u.] × d [km] / Ra
[km] )2
FluxRatio = FluxAsteroid [W/m2] / FluxSun
[W/m2]
and r [a.u.] is sun/asteroid distance, and d
[km] is asteroid/Earth distance = d [a.u.] × 1.496e8 [km]
and Ra [km] is the asteroids radius
Example #3: Faint Asteroid Geometric
Albedo Determination
When a Near Earth Asteroid passes close to Earth it may not be
possible to obtain the necessary SA-100 observations when the
asteroid is bright due to cloudiness or the asteroid's fast
motion. Days after closest approach observing opportunities might
be more favorable, but by then the asteroid will be fainter. In
this section I show a successful measurement of a 14th magnitude
asteroid's geometric albedo using the SA-100 mounted to the prime
focus of a Meade 14-inch telescope.
On 2014 Sep 20 I observed the main belt asteroid 1306 Scythia
(1930 OB) using my Meade 14-inch with a prime focus configuration
that employed a HyperStar lens, a SBIG ST-10XME CCD and a SBIG
CFW10. The 10-slot CFW obscured 31% of the collecting area,
rendering the photons intercepted at the CCD equivalent to a
11.3-inch refractor or a 12.5-inch typical Schmidt-Cassegrain
reflector (with 13% blockage). A few days earlier I had
calibrated the sun-like star 51 Peg using a Celestron 11-inch
telescope to compare its SA-100 flux spectrum to Vega's SA-100
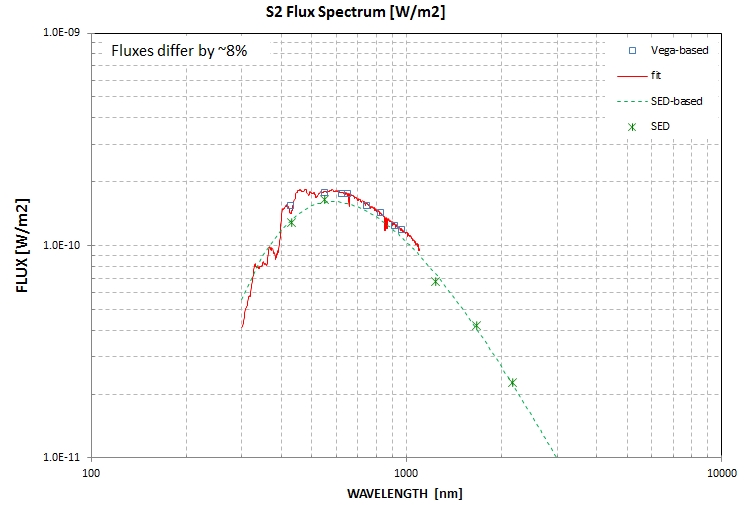
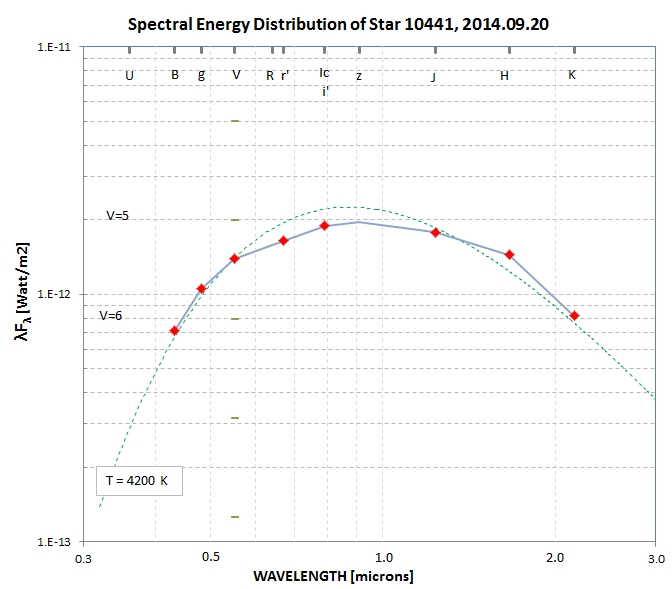
spectrum using a 5% aperture mask. Here's the SED I derived for 51
Peg:
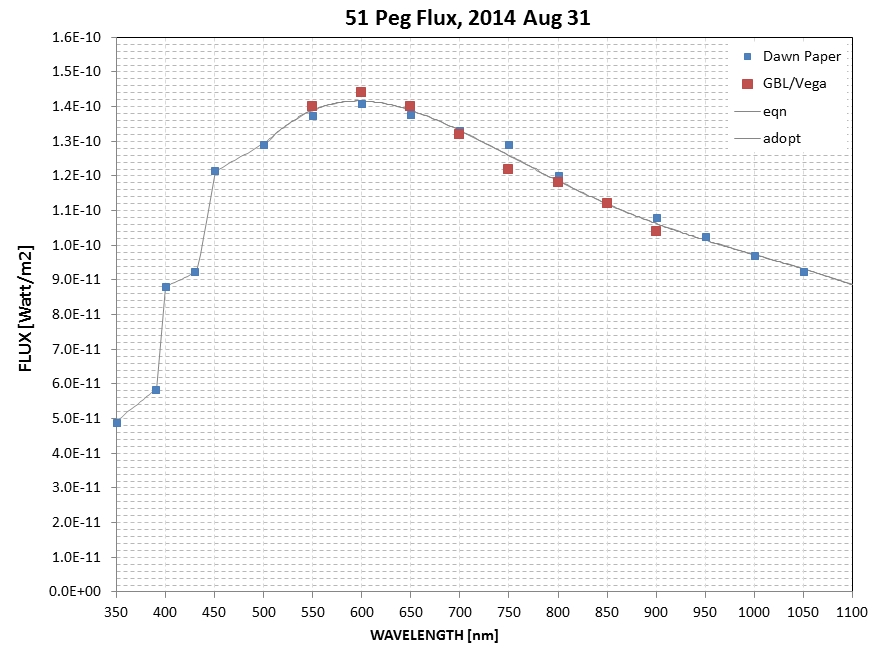
There is excellent agreement between the 51 Peg SED adopted by
Schroder et al (2013) and the one I measured on Aug 31 using the
SA-100.
My observations of Scythia on 2014 Sep 20 with a Meade 14-inch
were sub-optimal because the Meade's prime focus FOV was 71 x 48
'arc, with an image scale of 1.95 "arc/pixel, which produced a
crowing of stars and their SA-100 spectra, as shown by the next
sample image:

Several 9-image median combine images were measure using the
MaxIm DL profile tool, and each was processed in a spreadsheet to
produce "raw spectra" shown here:
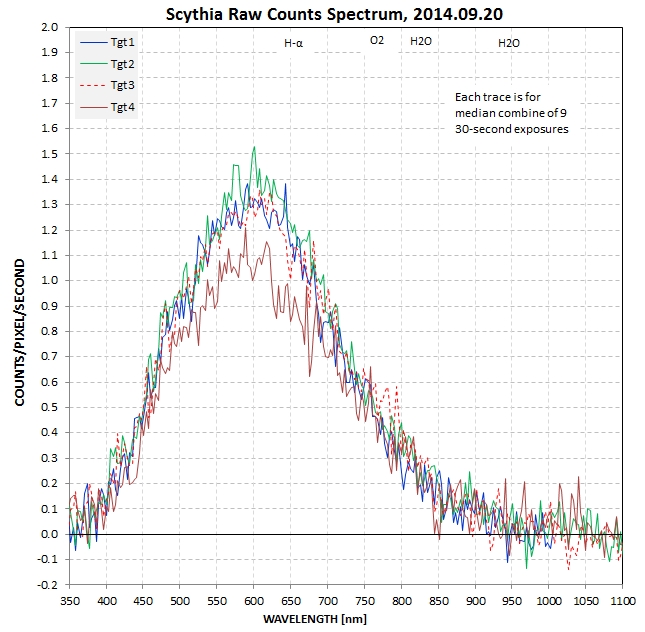
Cirrus clouds were present so one of the raw spectra (red trace)
may be low due to transient cloud losses.
Path 1: At this point there's a divergence of
analyses of the Scythia SA-100 data. The first path will make use
of the traditional "all-sky calibration method, and later I'll
resume from this stage of analysis using the differential
calibration method.
Scythia was only 3.3 degrees from 51 Peg, so my observations of
both fields were automatically at about the same air mass (all at
an elevation of ~ 71 degrees).
The ratio of Scythia to 51 Peg was multiplied by my adopted SED
for 51 Peg to produce the Scythia SED in the following:
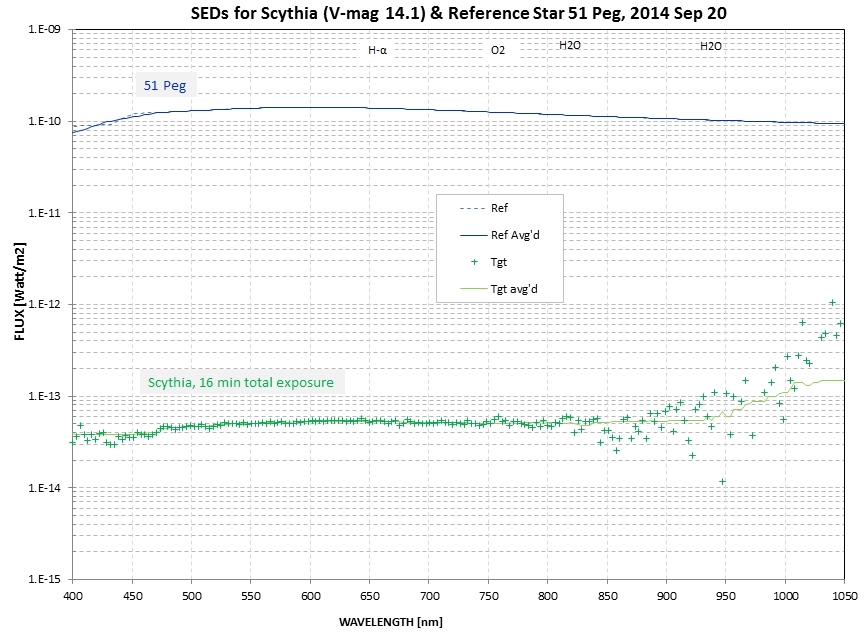
Figure 14. SEDs for 51 Peg and asteroid Scythia, taken
at the same air mass and approximate same time with the
Meade 14-inch telescope.
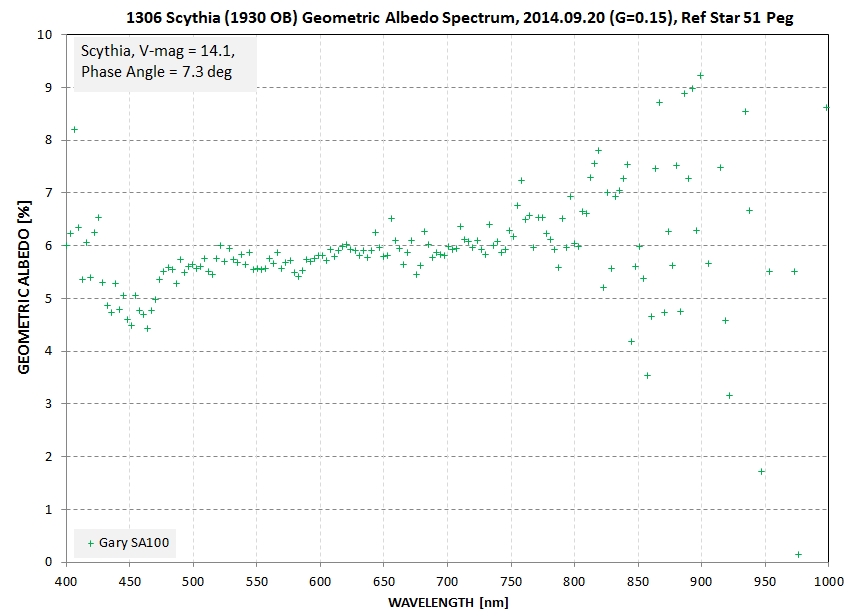
Converting an asteroid's SED to geometric albedo involves dividing asteroid SED by the sun's SED, and entering the result in an equation described in the previous section. For Scythia, using 51 Peg for an all-sky calibration just described, the geometric albedo result is shown in the next figure.



Converting SA-100 Flux Spectrum to
Magnitudes
There's a relationship between flux and magnitudes, given by the
following equation and table (described in detail at link):
λFλ [W/m2] = SED Constant × 10-0.4 Mag
| Band |
Effective Wavelength [micron] |
SED Constant [W/m2] |
| B |
0.433 |
2.954E-8 |
| V |
0.550 |
2.091E-8 |
| Rc |
0.640 |
1.443E-8 |
| Ic |
0.790 |
0.968E-8 |
| g' |
0.481 |
2.48E-8 |
| r' |
0.670 |
1.75E-8 |
| i' |
0.790 |
1.40E-8 |
| z' |
0.910 |
1.22E-8 |
| J |
1.235 |
3.869E-9 |
| H |
1.662 |
1.847E-9 |
| Ks |
2.159 |
0.926E-9 |
Since we know the flux spectrum for asteroid Scythia (Fig. 14) we
can determine magnitudes at these standard bands (by solving the λFλ equation
for "Mag"). Below is a plot of filter response functions for these
bands, which we must convolve with the asteroid spectrum in order
to get a response-weighted flux.

Notice that the filter response functions take into account CCD
QE function and telescope corrector plate transmission function.
The filter response weighted asteroid fluxes yield the following
magnitudes:
B = 14.52
V = 14.09
g' = 14.31
r' = 13.93
i' = 13.67
z' = 13.52
Here's another way to present these mag's:
This plot is another way of showing that Scythia has increased
albedo at longer wavelengths 'i & z').
Standard Filter
Measurements: Evaluating SA-100 Magnitudes with Conventional
Measurement Method
On the same night that the SA-100 was used to observe Scythia a
set of measurements was also made with filters g'r'i'z'. The
magnitudes determined using these filters can be compared with the
SA-100 magnitudes determined from the flux spectrum in order to
evaluate the quality of magnitudes inferred from SA-100
observations.
g' = 14.28 ± 0.01 vs 14.31 SA-100
(dif = +0.03)
r' = 13.75 ± 0.01 vs 13.96
SA-100 (dif = +0.21)
i' = 13.48 ± 0.01 vs 13.87
SA-100 (dif = +0.39)
z' = 13.42 ± 0.02 vs 13.77
SA-100 (dif = +0.35)
The g' magnitudes agree well, but the others differ by ~ 1/3
magnitude. I think this is probably going to be a realistic
assessment of the much lower quality of SA-100 based magnitudes
compared with the traditional ones using filters.
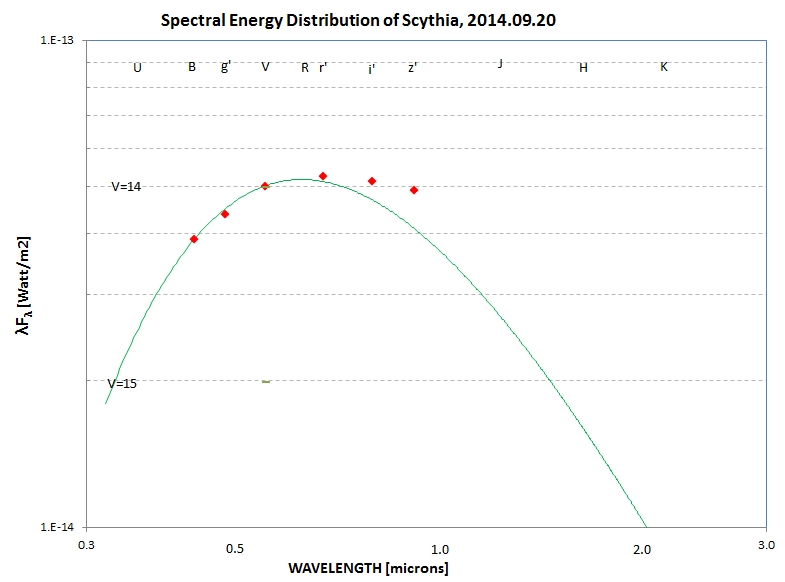
Here's a SED for Scythia based on the high quality g'r'i'z'
magnitudes:
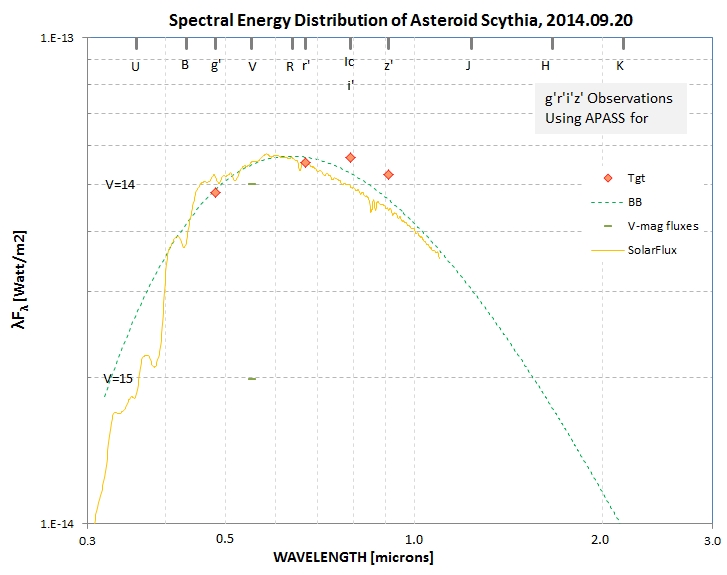
To satisfy my curiosity about the suspicious-looking SED for the
Reference Star 10441 (c.f., Fig. 16), I derived good quality
measurements of it using the g'r'i'z' filters. Here's how my high
quality magnitudes compare with the APASS ones in a SED plot:
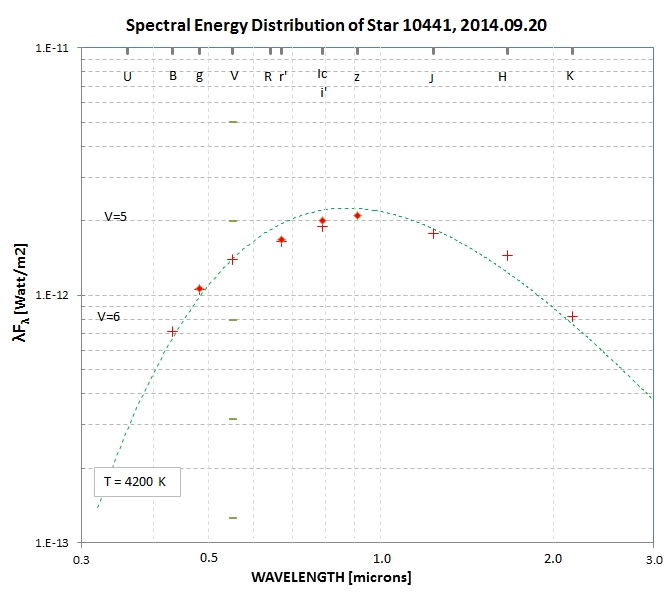
I conclude that this star simply departs from a blackbody
spectrum in a way that renders it problematical for use as a
reference star for calibrating SA-100 spectra. This underlines the
misgivings I have for using background stars for differential
photometry calibration. The safest procedure for calibrating
SA-100 observations is to use a well-calibrated secondary standard
stars using the all-sky photometry method. So far I've used Vega
as a primary standard to calibrate 59 Vir, beta CB, tau Vir, 109
Vir and 51 Peg. I need to emphasie stars near the ecliptic for the
winter season. When this project has progressed I'll present their
spectra at a web page devoted to reference stars for SA-100
calibration, and link to it at this web site.
![]()
This site was opened 2014.09.06. Nothing on this
web page is copyrighted. BGary web sites