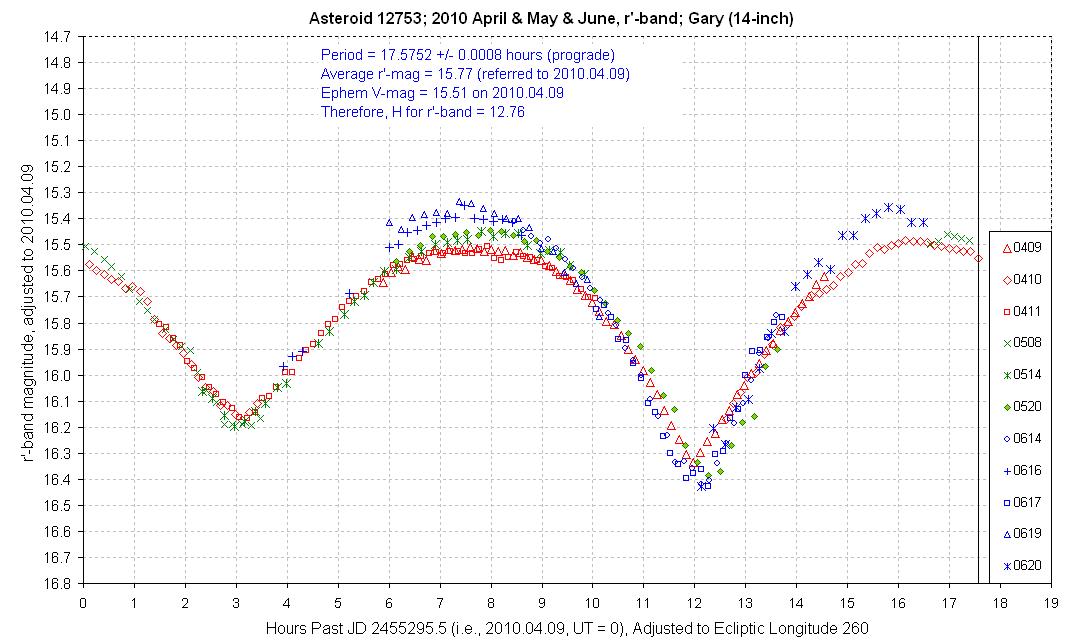
Figure 2010.01. All masurements during the 2010 opposition, with magnitude adjustments corresponding to 2010 April 9. The "before" opposition data are red, the "during" opposition data are green, and the "after" opposition data are blue.
Asteroid 12753 Povenmire probably belongs to the Eunomia family (based on its semi-major axis and eccentricity). My all-sky calibrations argue for a revised H = 12.81. Diameter can only be estimated by assuming albedo; if albedo = 5, 10 and 20% we calculate diameters = 16.3, 11.5 and 8.1 km. Colors are B-V = 0.78 ± 0.08, V-R = 0.60 ± 0.04 and R-I = 0.33 ± 0.06. The rotation period is 17.5752 ± 0.0008 hours, based on rotation light curves for 2010 April, May and June (earlier rotation light curve foldings may be flawed). The peak-to-peak brightness range is ~1.0 magnitude, and varies slightly with viewing geometry. This constrains the ratio of major to minor axis diameters to > 2.5. This web page will illustrate a pitfall that had me fooled for several years, and I hope it can serve as an instructive example on where care must be taken in analyzing rotation light curves taken over an interval greater than a few weeks.Links Internal to this web page:
This web page is devoted to my observations of asteroid "12753 Povenmire."
They began in the Fall of 2003 when I measured the rotation period and
V-Rc and R-Ic colors. More accurate observations were made in 2006 of
the asteroid's B, V, Rc and Ic magnitudes (2006.05.31). During the 2008/2009
opposition better quality measurements called for a revised period of 17.56
hours, with a slight preference for "retrograde" rotation. The 2010 opposition
occurred with the asteroid closer to Earth and at a higher declination,
and observations were made using better hardware and improved observing
and image analysis procedures. During this opposition the orientation of
the asteroid's rotation axis was more favorable, causing a greater variation
in brightness during each rotation. My plan is to add results of additional
observations to this web page, inserting them as a new section "at the
top" (immediately below this section).
The reader may wonder why I am devoting effort to this asteroid. The answer
is that I decided in 2003 that I wanted to learn about asteroid observing
by selecting one challenging asteroid for a concentrated observing project.
By coincidence, I met Hal Povenmire at the same time, and he had just
had an asteroid discovered by the Palomar Observatory 18-inch Schmidt
telescope was named for him. At Hal's suggestion I "adopted" his asteroid
for my first asteroid project. This web page is an outgrowth of that decision
and it is my way of finding out how much can be learned about an asteroid
using an amatuer telescope. It also has served to demonstrate pitfalls that
have rightly humbled me (described in the next section).
The last section describes my first floundering attempts at asteroid
observing, and it now seems "bloated" to me. At the time, however, all entries
seemed relevant since I didn't know what things had to be worried about.
I am leaving it in all its bloated form as an example of what beginners
worry about as they work to hone their observing and analysis techniques.
It is possible that other amateurs beginning the asteroid observing odyssey
may benefit from it.
The 2010 opposition was "higher in the sky" for me, and the asteroid was
~ 1.4 magnitude brighter than for the previous opposition. Two other factors
contributed to higher quality observations: 1) improved hardware (more sensitive
CCD camera, r'-band filter, dome-based), and 2) better observing and image
analysis procedures (better image alignment, smaller photometry apertures).
Folded Rotation Light Curves
Asteroid 12753 Povenmire was observed for about a week before opposition
(April), another week at opposition (May), and a week after opposition (June).
The next figure shows all measurements, with magnitude adjustments that
correspond to 2010 April 9.

Figure 2010.01. All masurements during the 2010 opposition, with
magnitude adjustments corresponding to 2010 April 9. The "before" opposition
data are red, the "during" opposition data are green, and the "after" opposition
data are blue.
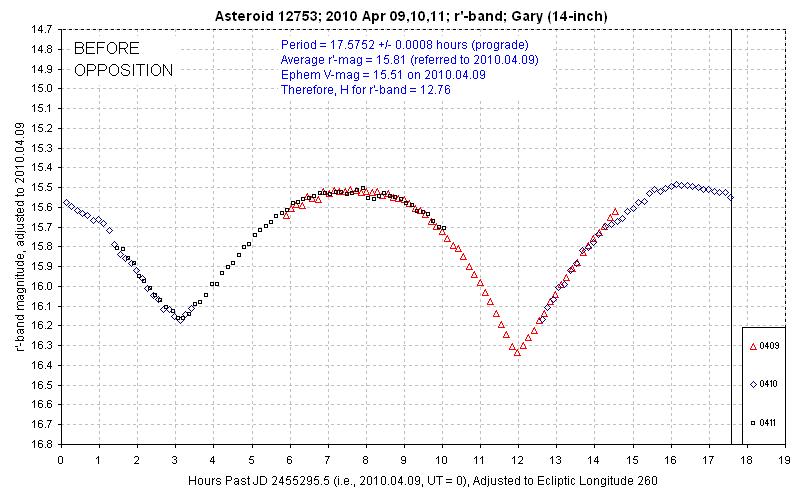
Figure 2010.02. April data, before opposition.
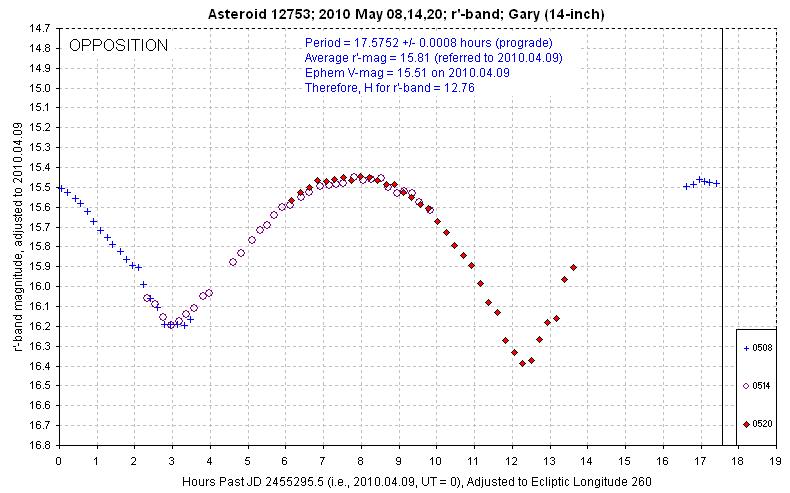
Figure 2010.03. May data, during opposition.
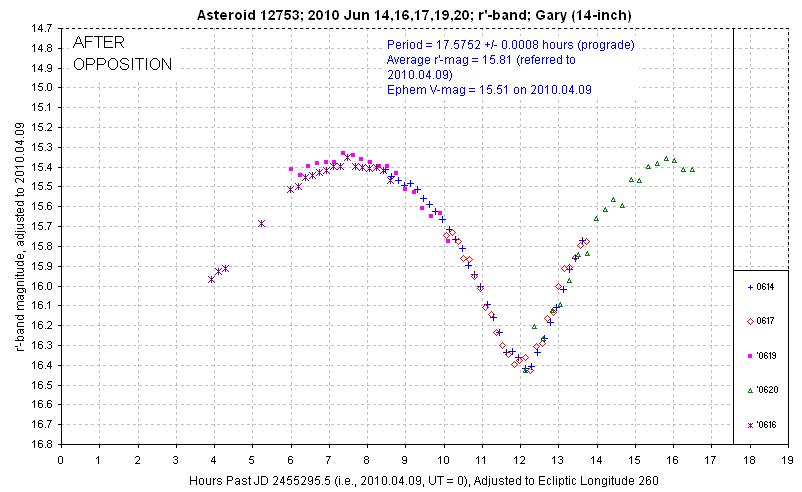
Figure 2010.04. June data, after opposition. Note that near the
summer solstice the nights are short and it's difficult to obtain a complete
rotation light curve.
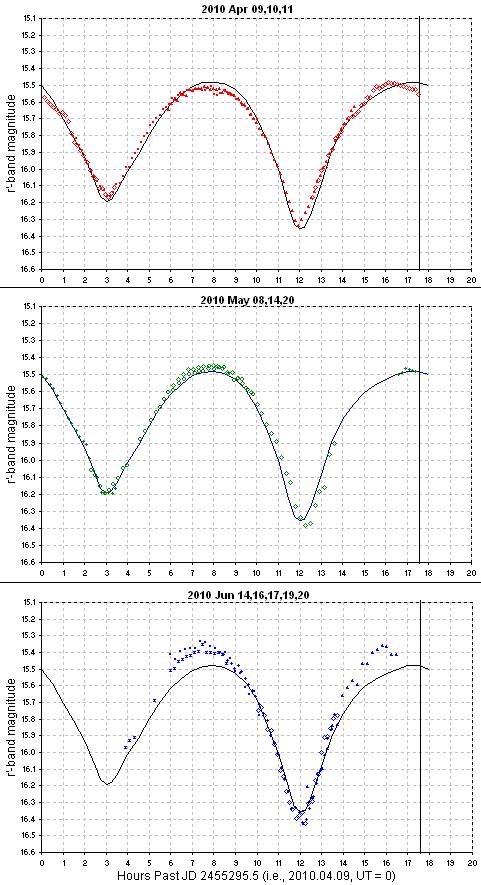
Figure 2010.05. Before, during and after panels superimposed
on the same "reference fit" showing the smooth evolution of the rotation
light curve shape.
Viewing Geometry
The interpretation of light curve observations during an opposition should
take into account at least two viewing geometry angles. One is related to
the Earth observer's view of the asteroid with respect to the asteroid's rotation
axis (fixed to the stars), and the other relates to the direction of the
sun's illumination of the asteroid in relation to the observer's view (the
phase angle). The next figure shows the relevant geometry for the three observing
times for the 2010 opposition.
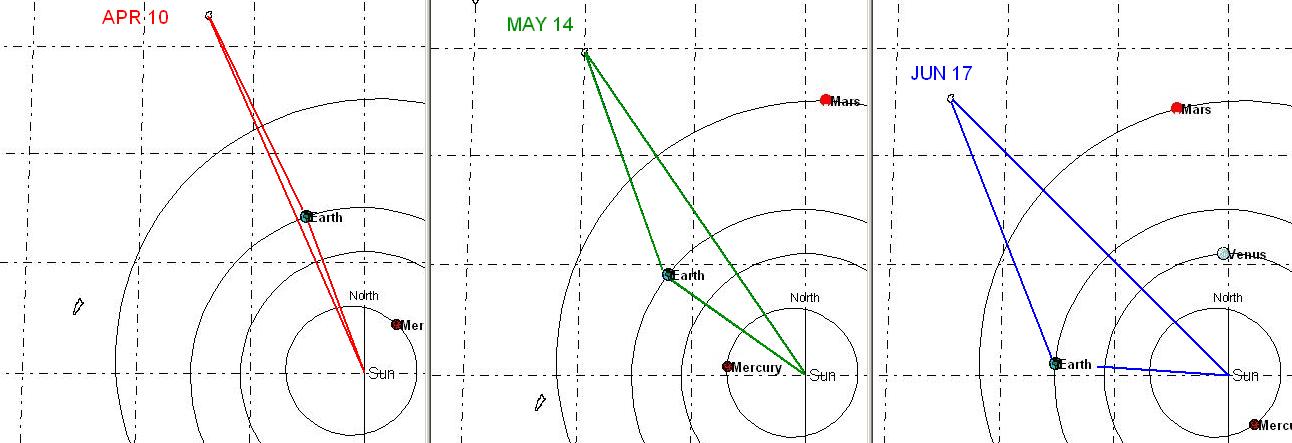
Figure 2010.06. Viewing geometry for the three observing times
in 2010, projected on the Sun-Earth-asteroid plane.
For each of the observing dates during the 2010 opposition the lines between
the Earth and asteroid point in almost the same direction. Another way to
say this is that the apparent RA/DE of the asteroid was almost the same for
all observations. Between Apr 10 and Jun 17 the change was 11 degrees.
On Apr 10 the asteroid was almost fully illuminated by the sun, and back-scattering
should have been maximum; after this date the direction of illumination was
increasing from the asteroid's right side (as viewed by an Earth observer).
Because the asteroid was above the ecliptic plane during the observations
it was never 100% illuminated (i.e., the phase angle never was zero). The
phase angle, Sun-Target-Observer (STO), was never less than 11 degrees. For
the three observing dates STO = 11, 16 and 24 degrees.
The viewing geometry can be summarized by stating that during the 2010
observations the Earth's view of the asteroid changed by 11 degrees and the
sun's illumination of the asteroid in relation to the Earth's view of it
(phase angle) changed 13 degrees. Both viewing geometry changes should be
considered as contributing to differences in the rotation light curves for
April, May and June. The small change in the Earth's view of the asteroid
(11 degrees) means that only small adjustments are needed for deriving a
rotation period from the varying viewing geometry. Another effect of the
small change in viewing geometry is that distinguishing between prograde
and retrograde rotation will be difficult since the period solution for both
possibilities will be close to the same. However, it should be possible to
constrain rotation direction by comparing the "phase" of the RLC for 2010
rotation with the phase from a previous opposition. But even this comparison
is subject to a possible ambiguity. If the other opposition occurs at exactly
the opposiste season then adding or subtracting a half rotation, corresponding
to the cases of retrograde and prograde corrections, will be equally consistent
with the observations. The best comparison is with oppositions whose seasons
are 3 months apart because adding or subtracting 1/4 rotation will have significant
differences when comparing RLCs. Here's a table of opposition dates for the
past 8 years.
OPPOSITION DATES
| Year |
Mo&date |
Mo# |
Year.fr |
dt |
dt' |
| 2010 |
Apr 17 |
4.6 |
2010.30 |
0.00 |
|
| 2008 |
Dec 09 |
12.3 |
2008.94 |
1.36 |
0.11 |
| 2006 |
May 29 |
5.9 |
2006.41 |
3.89 |
0.14 |
| 2003 |
Oct 15 |
10.5 |
2003.79 |
6.51 |
0.49 |
The interval between oppositions is not uniform because the asteroid's
orbit is eccentric; lately it was in the range 1.36 and 2.62 years. The last
column in the above table can be used to identify which oppositions can be
used to constrain the solution for prograde versus retrograde. For example,
the previous opposition occurred 0.36 years apart (after subtracting the
integer), and this differs from 0.25 by 0.11 year, so the RLC for these two
oppositions can be used to distinguish between prograde and retrograde. In
addition, the period can be refined by such a comparison.
Analysis
Observing asteroids may be easy, but extracting a correct "rotation light curve" is more difficult than I ever imagined. I thought exoplanet transit observing was difficult, but I'm beginning to think asteroids are a greater challenge. In 2004 I published a paper (in Minor Planet Bulletin) based on observations during the 2003 opposition of asteroid 12753 Povenmire. One of the purposes for the paper was to show how an asteroid can be observed in a star-dense field using a "star subtraction" procedure. That aspect of the paper is still valid, but an asteroid spends most of its time away from star-dense parts of the sky. Other observing procedures are therefore more appropriate for use for most of an asteroid's journey across the sky. I am indebted to Brian Skiff for suggesting several observing and analysis tips in November, 2008 that are appropriate for most asteroid observing situations. I'll present those tips in another section, but in this one I want to illustrate a surprise that awaited me when I used Brian Skiff's suggestions for 12753 Povenmire. My 2004 paper gave a rotation period of 12.854 ± 0.001 hours. What a surprise, then, when I measured 13.2 hours from the December, 2008 observations and 17.56 hours from the January, 2009 observations! Could the asteroid's rotation be slowing down due to an outgassing plume at one corner? Then I reprocessed the December data using the better-constrained January period and found that the 13.2 hour period was just one of many possible ones, and 17.6 hours was also compatible with that data. My task now is to re-process all observations before 2008 to see if month-long data groups are also compatible with 17.6 hours. But first, view the next three plots to see how important it is to restrict data groupings to month or shorter intervals.
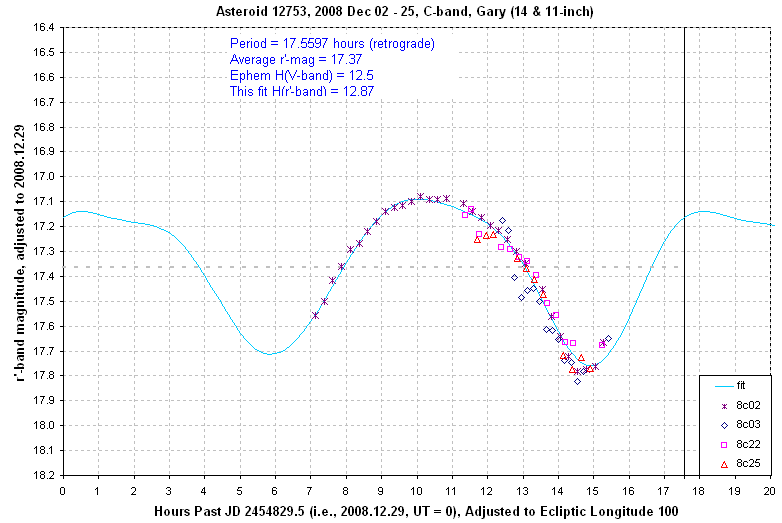
Figure 2008.01. In December, 2008 I obsaerved on 4 dates and
created this RLC, with a tentative period of 17.6 hours (before opposition).
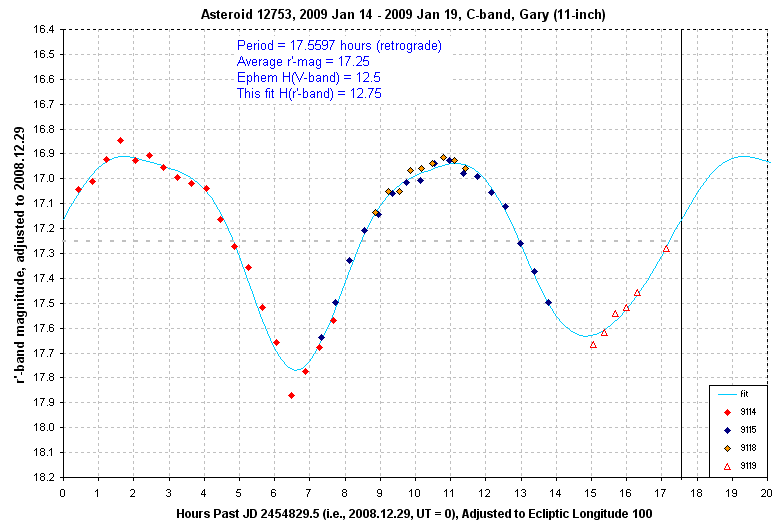
Figure 2008.02. A month later I observed on another 4 dates
and obtained this better-constrained RLC solution (after opposition).
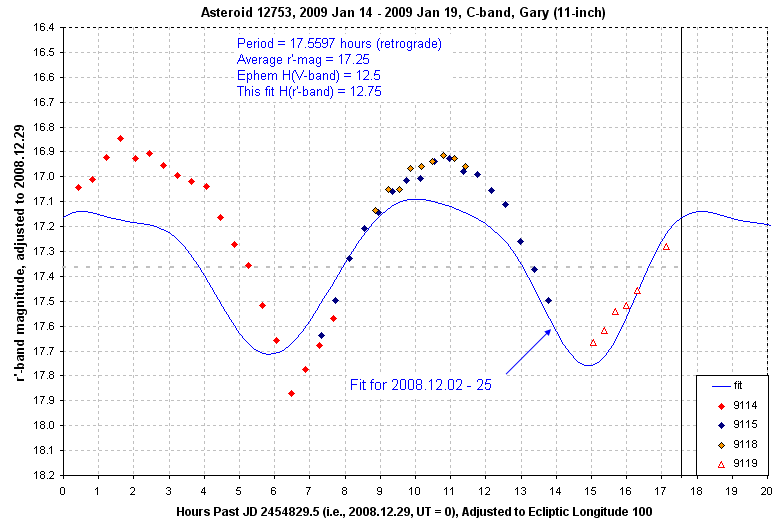
Figure 2008.03. Here's the same data as above (Early January)
and the RLC solution for a month earlier.
These three plots show that RLC shape and amplitude change with viewing
geometry on a timescale as short as a month. This means it is unwise to
try to create a RLC from observations spanning more than a month (assuming
viewing geometry is changing fast, as it does near opposition). During the
2-month interval for these observations the asteroid was viewed from essentially
the same direction, but the sun's illumination of the asteroid changed.
The sun-target-observer changed from 2 degrees in early December to 16 degrees
in mid-January. This must be the explanation for the RLC change during that
time.
As my observing technique improves I am able to produce better quality
rotation light curves. The 2008/2009 opposition will benefit from improvements
in magnitude calibration and SNR. The magnitude calibration is based
on Carlsberg Meridian Catalog stars, which are present at most declinations
where asteroids are located. Virtually all stars brighter than 14th magnitude
in r'-band are present in this catalog with sufficient accuracy (~0.04)
for use in comparing one night's observations with those from another night.
This greatly facilitates combining of observing session data from many
nights. Improved SNR is achieved by not using the star subtraction method
and instead usng a small aperture and identifying when backgound stars
produce apparent brightenings. Each apparent brightening will have a width
given by the photometry aperture, which is kept small (~1.6 x FWHM), and
animations can be used to verify that a brief brightening is due to passage
of the asteroid in front of the background star.
Re-Processing
Pre-2008 Observations
What You Can Learn
From the Orbit
I have been surprised by how much can be learned about an asteroid from
its orbit. Here are some (osculating) orbital elements for 12753 Povenmire
(for the 2003 epoch):
a = 2.62334 a.u. (semi-major axis)
i = 14.80 (inclination)
e = 0.148129 (eccentricity)
Consider how this orbit compares with a scatter plot of orbit elements
for main belt asteroids.
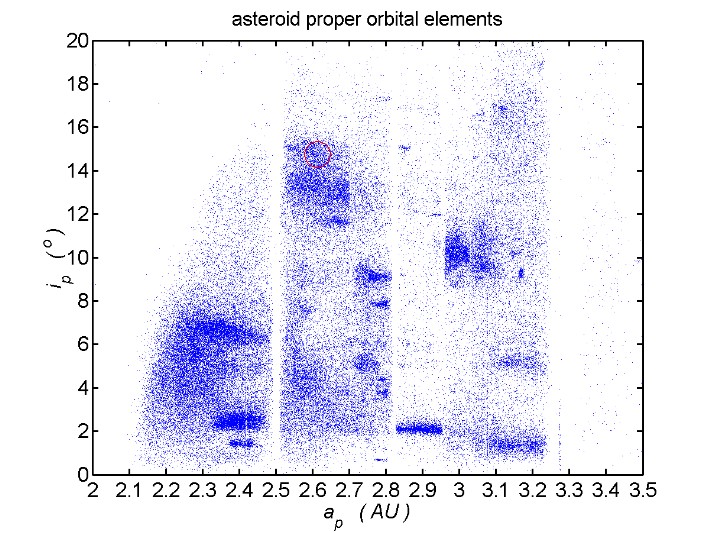
Figure 1. Scatter plot of the proper elements inclination versus semi-major axis for 96,944 main belt asteroids. The clumps are asteroid "families." The red circle corresponds to asteroid 12753's orbit. The Kirkwood gaps at 2.50 and 2.82 a.u. divide the main belt into Zones I, II and III. (Plot created by Piotr Deuar, appearing in Wikipedia).
In this figure it can be seen that asteroid 12753 Povenmire is in the
main belt Zone II, at a high inclination associated with an asteroid family.
It's also possible to see family associations in a scatter plot of i versus
e, as shown in the next figure.

Figure 2. Scatter plot of the proper elements inclination versus eccentricity. The red oval is "located" at asteroid 12753's orbit, with the dimensions corresponding to typical variations over millions of years for a main belt asteroid. (Plot created by Piotr Deuar, appearing in Wikipedia).
Again, the asteroid 12753 Povenmire appears to be associated with a couple
main belt asteroid families. It should be noted that an asteroid's current
epoch (Keplerian element) i and e will differ from its long-term average
("proper" element) i and e. Typical variations over millions of years
have been calculated by Piotr Deuar (Wikipedia) to be 0.03 (eccentricity),
0.7 degrees (inclination) and <0.02 a.u. (semi-major axis). These uncertainties
are represented by the red oval in the above figure.
Finally, there's one more scatter plot to show: e vs a.
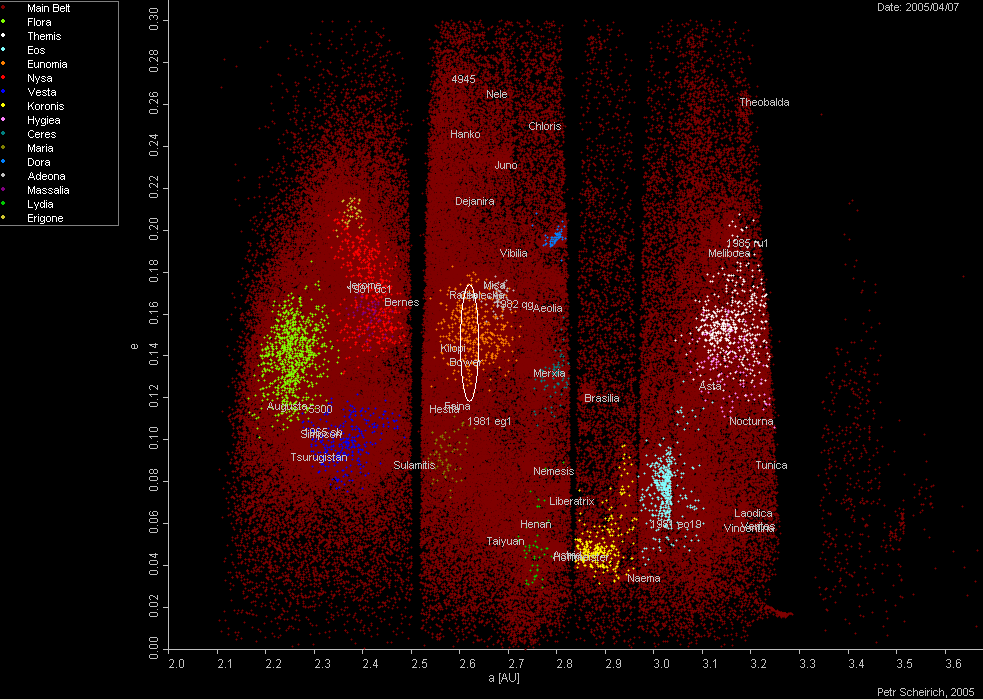
Figure 3. Proper element e versus a, with an oval showing asteroid
12753's location. (Plot created by Petr Scheirich, 2005, Wikipedia)

On May 31, 2006 I observed asteroid 12753 Povenmire with a 14-inch Meade
RCX400 telescope during a 2.5-hour session on 2006.05.31. Since this
asteroid rotates with a 12.85-hour period and a 0.23 magnitude amplitude
(1/2 of peak-to-peak), the brightness will vary in a way that is approximately
represented by a sinusoid with a period of 6.42 hours (1/2 of 12.85 hours).
This means that during a 2.5-hour observing session the brightness for each
filter band could change by almost 0.46 magnitude (2 * 0.23 magnitude).
The observing session consisted of BVRcIc followed by another such set.
The B, Rc and Ic magnitudes were offset in such a way that the entire set
of magnitudes matched a sinusoidal model having the expected amplitude
with an arbitrarily chosen phase. The model's average V-magnitude was also
adjusted to achieve agreement with the osbrevations. Here's the final set
of BVRcIc magnitudes with the model fit.
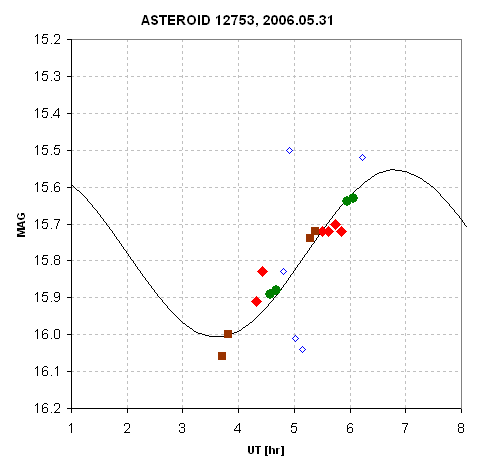
Figure 6. Magnitudes after adjustment of B, Rc and Ic to agree
with V using the rotation model determined in 2003. The model is for
a rotation period of 12.854 hours and amplitude 0.227 magnitude; the average
V-magnitude and phase shift were adjusted to agree with the data.
The sinusoidal period-averaged V-magnitude is 15.78 +/- 0.08. The following
colors were measured from required offsets required to produce the above
figure:
B-V = 0.78 +/- 0.08
V-R = 0.60 +/- 0.04
R-I = 0.33 +/- 0.06
The period-average magnitudes for all filters is given here:
B-mag = 16.56 +/- 0.10
V-mag = 15.78 +/- 0.08
Rc-mag = 15.18 +/- 0.09
Ic-mag = 14.85 +/- 0.10
These magnitudes are not based on observations of a Landolt area during
the same night's observing session, as is my usual custom. Instead, I
established calibration star magnitudes using two other methods: 1) use
of "simplified magnitude equations" and telescope system photometry constants
from previous osberving sessions, and 2) USNO-A2.0 B and R magnitudes
for stars in the asteroid image's star field. Both methods gave essentially
the same result, with differences of 0.06, 0.02 and 0.02 magnitude for
B, V and R. The first method is described at SME. The second method
is described at USNO.
Is there anything unusual about the asteroid's color? Not much, as the
next two figures show.
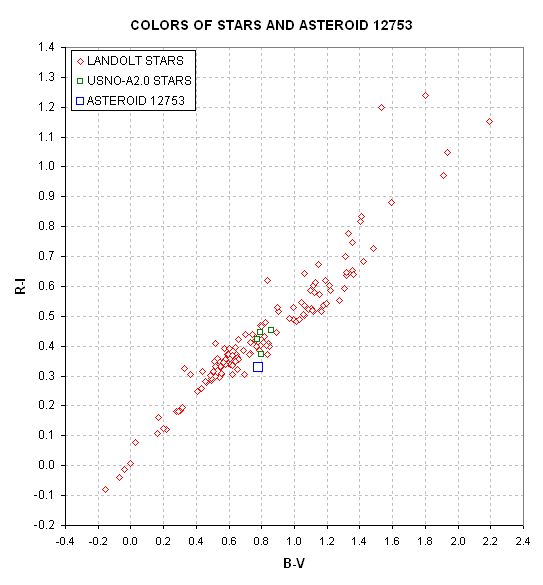
Figure 7. Colors of typical stars and the asteroid 12753. Landolt
stars are small red diamonds, the 4 USNO-A2.0 stars used as reference
standards for the FOV of the 2006.05.31 images are small green squares,
and the asteroid 12753 is the large blue square.
In this figure we plot the "color slope" in the red/infrared region versus
"color slope" in the blue/green region. Since stars have a brightness
versus wavelength distribution that is close to a "black body" spectral
distribution their color slopes fall along a straight line in this type
of figure. The asteroid's I-band brightness appears to be fainter than
expected (if it were a star) by ~0.1 magnitude (10%). If you're wondering
about the alternate interpretation of this plot, that B-V is unusual instead
of R-I, consider the next figure.
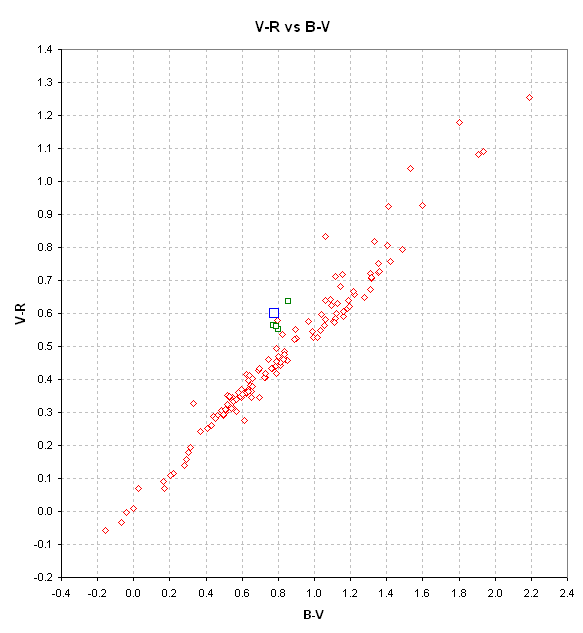
Figure 8. Color slopes V-R versus B-V for typical stars and
the asteroid 12753. Landolt stars are small red diamonds, the 4 USNO-A2.0
stars used as reference standards for the FOV of the 2006.05.31 images are
small green squares, and the asteroid 12753 is the large blue square.
This figure shows that the asteroid's brightness versus filter band is
the same as typical stars for the filter bands B, V and Rc. Therefore,
the small anomaly in the previous figure is due to the asteroid's anomalous
I-band brightness. (This result is different from the 2003 opposition,
which showed a drop in brightness for V with respect to R; these BVRcIc
colors have to be re-observed).
I am not going to speculate on the meaning of the asteroid having a slightly
low albedo at I-band because I don't know what it means. Learning about
this will be a future project.
For this date the ephemeris predicted V-mag, based on H = 12.5, was 15.33.
Since the asteroid was observed to be 0.31 magnitude fainter I recommend
revising H to the value:
H = 12.95 +/- 0.08
This suggested value for H is in approximate agreement with 12.8 made
in 2003 (described below). My weighted average estimate is
H = 12.9 +/- 0.1.
As an aside, astrometry was performed on 15 groups of 5 median combined
images with the following result.
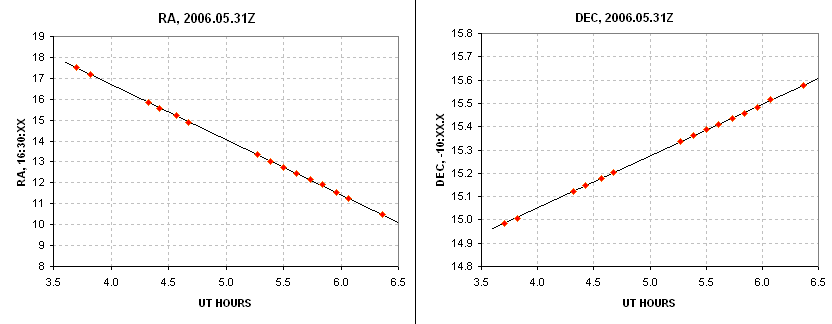
Figure 9. Astrometry solutions for RA [sec] and Dec ['arc].
RMS scatter is 0.33 and 0.20 "arc.
The RA and Dec locations agreed with the MPC ephemeris to within the MPC
round-off error. The orbit for this asteroid is very well determined.
Rotation
Light Curves and Period Solution from 2003 to 2007 Observations
This Section Will Be Removed and Replaced With
Another Re-Processing Analysis in Due Time
The following 12 "rotation light curves" are corrected for viewing geometry.
For example, if the asteroid is rotating retrograde (which is the solution
arrived at from these LCs) after opposition the asteroid has to rotate
an extra amount to be viewed by earth the same as viewed from the sun.
Before opposition the asteroid presents the same view to earth observers
before it is presented to the sun. When the sun is used for this reference
the period solution will differ slightly from what would be found if the
stars were used as a reference; the difference is miniscule since the two
periods will have a ratio equal to the ratio of the rotation period to the
orbital period (i.e., about 1 part in 3000).
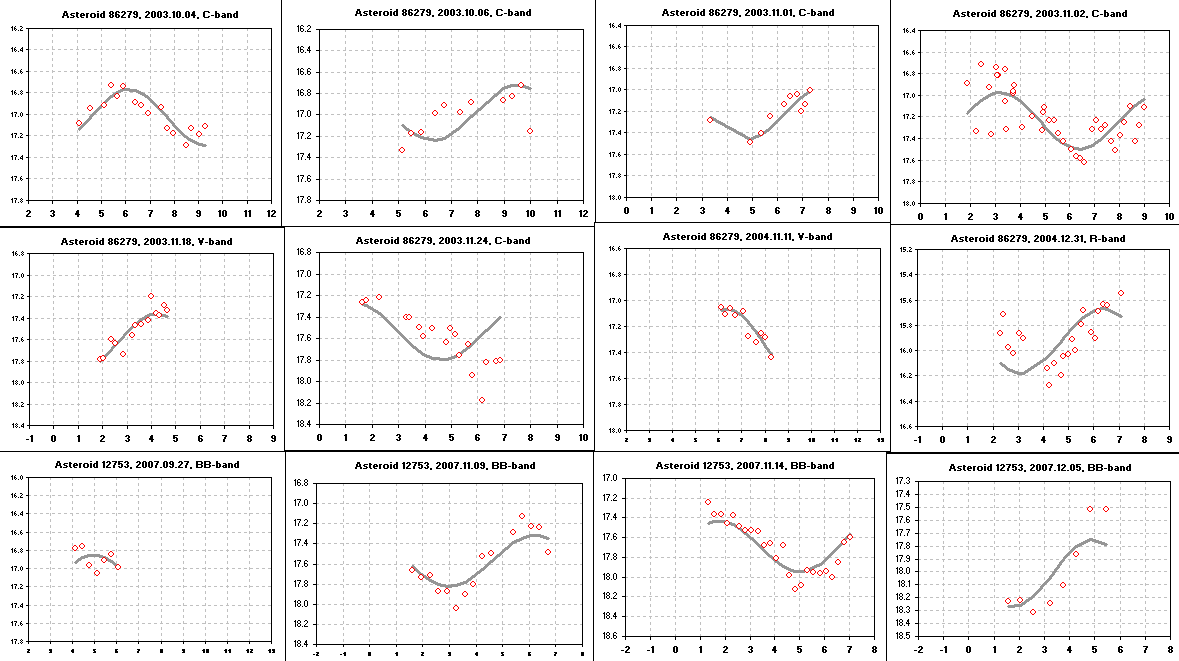
Figure 2007.01. The "model" in these 12 panels has a period of
12.85752 hours and an amplitude for the first harmonic (half the period)
of 0.258 magnitude (half of peak-to-peak).
The last panel has the suggestion that the amplitude is larger than the
model fit for all observations. This might be a correct situation because
the model does not allow for a rotation axis that is inclined to the
orbit. To illustrate the potential importance of this, consider a rotation
axis that's tilted such that when the observing geometry causes observers
on earth to see the asteroid at RA ~23 hr, for example, the rotation axis
is perpendicular to the line-of-sight, observations on dates when RA ~23
hr will exhibit a larger amplitude than at other times. During the 2007
observations the asteroid's RA ~23 hr, and according to the 12 panel display
all the 2007 observations appear to have a larger amplitude of variation.
All of the previous opposition's observations (in 2004) were made when RA
~07 hr. Only one of the panels has sufficient coverage to assess amplitude,
and it indeed is close to the model fit amplitude. The first opposition
(2003) was for RA ~1.5 hr, and since these observations dominate the solution
they exhibit amplitudes that are fit by the model. The next opposition will
occur in early December, 2008, when RA ~05.1 hr. At that time it will be
at a higher declination (+16.4 deg), a given night's observations can be
longer (because the night's are longest in December), and the asteroid will
be much brighter than for any of the previously observed oppositions (V-mag
= 16.3).
Recall that the sections are arranged with the most recent results at
the top. This section treats the Minor Planet Bulletin, 31,
3 (2004) which is based on 2003 opposition observations. Here's a copy of
the article.
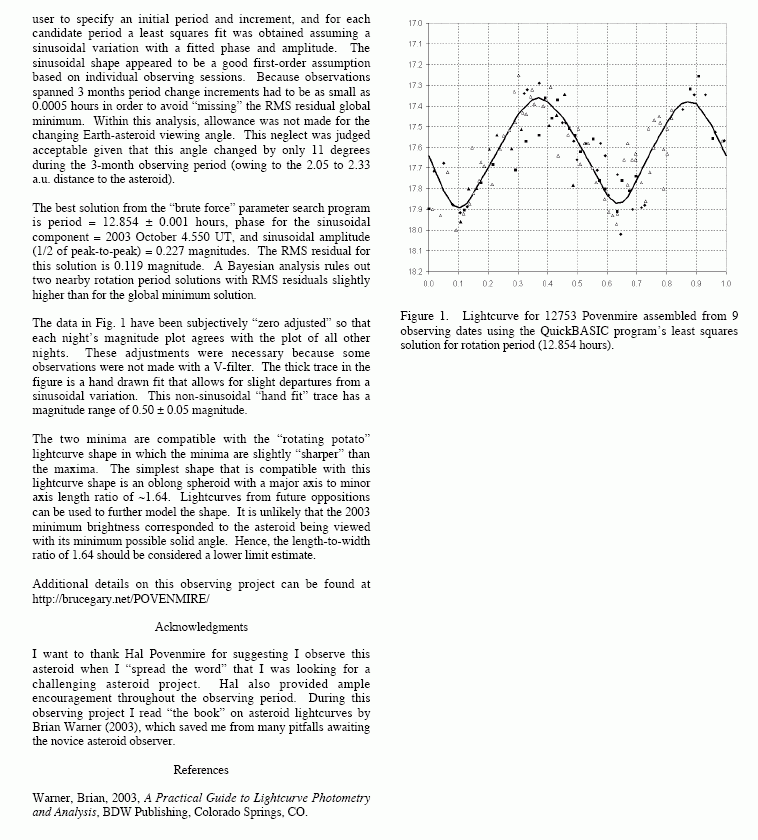
[This paper has an incorrect period of 12.854 +/- 0.001 hours. The correct
period is 17.56 +/- 0.03 hours. This has been a humbling learning experience.]
Rotation Period and
Shape (2003 Observations)
Observation Strategy Planning
I used a Celestron CGE 1400 (14-inch aperture, f/11, Schmidt-Cassegrain) telescope, a SBIG ST-8XE CCD, a SBIG AO-7 adaptive optics image stabilizer, a SBIG CFW-8 color filter wheel and JMI Smart Focuser. The telescope and detection system is mounted permanently in a sliding roof observatory in my residence back yard, located in sparsely-populated Hereford, AZ (Lat = 31.45265 degrees North, Lon = 110.23743 degrees West, altitude 4630 feet). My "seeing" point spread function FWHM typically ranges from 2.0 to 3.5 "arc (depending on exposure time). An unfiltered exposure of 4 minutes typically produces an image with a limiting magnitude of 20.0 (S/N = 3). Since the asteroid's magnitude was predicted to be 17.0 at opposition, the predicted signal-to-noise ratio, SNR, was ~50. This means the SE stochastic uncertainty should be ~2.3% for each 4-minute exposure (at opposition).
I suspect that the limiting factor for accurate measurements of brightness will be changes in extinction during a 10-hour observing session. If a reference star has a different color than the asteroid, then the ratio "asteroid/reference star" will vary approximately linearly with air mass (with the actual rotational light curve superimposed). One strategy to minimize extinction effects is to use a R filter (red), since extinction is smallest at the red end of the optical spectrum. This strategy incurs a siignal-to-noise, S/N, penalty of about 3, requiring approximately 9 filtered exposures to achieve the same S/N as an unfiltered exposure of the same duration.
An alternative strategy is to use only refernce stars that are known to have the same color as the asteroid. This strategy permits unfiltered exposures to be used, since both the asteroid and reference star will experience the same extinction amounts with air mass. I have tentatviely decided to adopt this strategy. Therefore, I will either pre-observe or post-observe the region through which the asteroid will move, using BVRI filters, and identify candidate reference stars that have the same approximate spectrum as the asteroid.
If I use my CCD at the Cassegrain focus, where images have a filed-of-view (FOV) with dimensions 11.2 x 7.5 'arc, the asteroids motion at opposition will be larger than the image. Since each night will require a completely new FOV, many reference star candidates will have to be studied during the course of the observations - assuming I use the CCD at the Cassegrain focus.
If I use the prime focus location for my CCD, the CCD images will have a greatly enlarged FOV. I have a HyperStar adapter lens for prime focus use, and it yields image dimensions of 72 x 48 'arc. The asteroid could be included in one image field for at least a half dozen consequtive nights. However, when the image scale is large, many interfering stars are likely to be located within any chosen reference annulus, which translates to larger systematic errors that will vary with the asteroid's motion. This is a potentially serious problem. Until I experiment with CCD exposures of star fields in the asteroid's part of the sky I will not know if this error source is important.
As an aside, it is commonly thought that fainter stars can be imaged using the prime focus than the Cassegrain focus due to the "faster" f-ratio. After all, at prime focus with my 14-inch Celestron the f-ratio is 1.86, whereas at Cassegrain it is f/11. However, prime focus is only "faster" for extended objects; it isn't faster for stars. The "speed" for stars depends upon the pixel width of star images. The same number of photons per second arrive at the star image on the CCD for both focus positions. If the width of the star is the same for both images then the signal-to-noise ratio will be the same (for a specific photometer signal circle radius, gap annulus width, and reference annulus width). Therefore, there is no advantage in observing faint stars at prime focus compared with Cassegrain focus. Not only will Cassegrain deliver more light to the CCD (due to absorption by the prime focus lens assembly), but fewer interfering stars are likely to be present in the signal circle and reference annulus.
Simulated observations of the star field at the asteroid's opposition location will reveal whether interfering stars in the reference annulus are likely to be a problem with the prime focus configuration. After a prime focus observing session it should be possible to decide whether to adopt the prime focus configuration or the Cassegrain configuration.
Initial Observations
The following color image shows a star field where the asteroid is supposed to be located. It was made using the prime focus (HyperStar) configuration, which affords a large 72 x 48 'arc FOV. The red, green and blue filter exposures were limited to 90, 90 and 180 seconds, so the faintest star have a visual magnitude ~16.0. Since the asteroid is predicted to be at Mv = 17.9 it will not be present in this image (within the circle in the figure). It is a coincidence that a high quality standard star is located about 1 degree from the asteroid (square in the figure). This star, Feige 16, has well-measured magnitudes (by Landolt), with Mv = 12.406. One purpose served by this image is to set the magnitude scale for the star field through which the asteroid will be moving for the next couple weeks.

Figure 2003.01. Color image of a star field containing the asteroid
(circle) and a calibration star (square). FOV is 72 x 48 'arc. [Celestron
CGE 1400, SBIG CFW-8, SBIG ST-8XE, red and green exposures 90 seconds,
blue 180 seconds; 2003 July 28, Hereford, AZ]
The calibration star, Feige 16 (square), has a bluish color, and this is borne out by its magnitudes. Most stars are saturated, and look white.
Unfiltered images were also made using the prime focus configuration. These will be useful in determining whether too many stars are present for obtaining star-free reference annuli.
The following animation is for a small portion of the prime focus FOV, but it does show the asteroid clearly, with the expected brightness and motion of 26 "arc durng a 1.3-hour interval.

Figure 2003.02. Movie sequence showing movement during a 1.3-hour
interval on July 28 UT. FOV is 20.8 x 13.5 'arc, northeast upper-left.
Magnitude ~18.0. The galaxy near the upper-right corner has a magnitude
of ~15.5. Each frame has a limiting magnitude of ~20.5. FWHM ~9 "arc.
[Celestron CGE 1400, prime focus HyperStar, f/1.86, SBIG CFW-8, SBIG
ST-8XE CCD; each frame consists of median combine of 13 60-second exposures,
unfiltered; 2003.07.28 UT; Hereford, AZ]
This image sequence illustrates how difficult it can be to select photometry apertures that do not include interfering stars in the reference annulus during a night's observing session. This can be seen better in the following figures, which are enlargements of the first and last images in the above sequence.
Figure 2003.03. Zoom factor of 5 of the first image in
the animation, showing a typical photometry annulus choice.
In this imge the inner signal circle contains essentially all of the asteroid's "light" and the outer reference annulus contains no interfering stars. This is an acceptable situation for photometry. For this case the asteroid's measured magnitude is ~18.0.

Figure 2003.04. Same zoom factor, but for the last frame in the animation, showing the presence of an interfering star in the reference annulus.
This image is unsuitable for photometry of the asteroid since the interfering star in the reference annulus would seriously alter the asteroid's apparent magnitude. This illustrates the main disadvantage of using prime focus for monitoring an asteroid's brightness for establishing its rotation period. Whereas the prime focus image scale is 2.81 "arc/pixel and FWHM is typically 9 "arc, the Cassegrain focus configuration provides an image scale of 0.44 "arc/pixel with FWHM typically 3.0 "arc. With a smaller FWHM it is possible to employ smaller photometry annuli, and thus reduce the likelihood of encountering interfering stars in the reference annulus. From now on I will use the Cassegrain focus configuration.
Accuracy of JPL Ephemeris
The following image shows the asteroid's location in relation to the JPL Ephemeris predicted location August 17.

Figure 2003.05. On 2003 August 17, 11:19 UT the asteroid's location
(intersection of two bars) is only 8 "arc away from a position predicted
by the JPL Ephemeris program (circle). Three stars with approximately
known magnitude are shown with labels that are 10 times the value of the
V-magnitude. The asteroid has a magnitude of 18.5. This image
is 7.2 'arc wide. North is up and east to the left. [Celestron
CGE 14-inch, JMI focuser, AO-7 adaptive optics, focal reducer yielding f/9.6,
SBIG CFW-8 color filter wheel, SBIG ST-8XE CCD; unfiltered, median combine
of 12 exposures, each 20 seconds long; Hereford, AZ]
The asteroid is positively identified from a blink sequence and its location is only 8 "arc away from the JPL Ephemeris predicted location. The (unfiltered) magnitude from this image is 18.5 +/- 0.1 (precision) +/- 0.2 (absolute uncertainty). The predicted (visual) magnitude is 17.7, so the asteroid appears to be 0.7 magnitudes fainter than predicted. More will be said about this below. The JPL Ephemeris has accurate orbital elements for this asteroid.
Preliminary Rotation Light Curve
The next figure is a 10-frame animation of the asteroid's motion on August 18 UT during a 3.6-hour observing interval.

Figure 2003.06. On 2003 August 18, from 07:58 to 11:41 UT, the
asteroid was imaged as it moved southeast. This image is 4.7 'arc square.
The faintest stars have a magnitude of 20.2 (S/N=5). The point-spread-function
has a FWHM of 3.3 "arc. The double stars are 5 "arc apart. [Celestron
CGE 14-inch, JMI focuser, AO-7 adaptive optics, focal reducer yielding
f/9.6, SBIG CFW-8 color filter wheel, SBIG ST-8XE CCD; unfiltered, each
frame is a median combine of 12 exposures, each 60 seconds long, guided
using the AO-7 adaptive optics autoguider; Hereford, AZ]
These 10 images have been used to establish apparent magnitude versus time for a 3.6-hour observing interval.
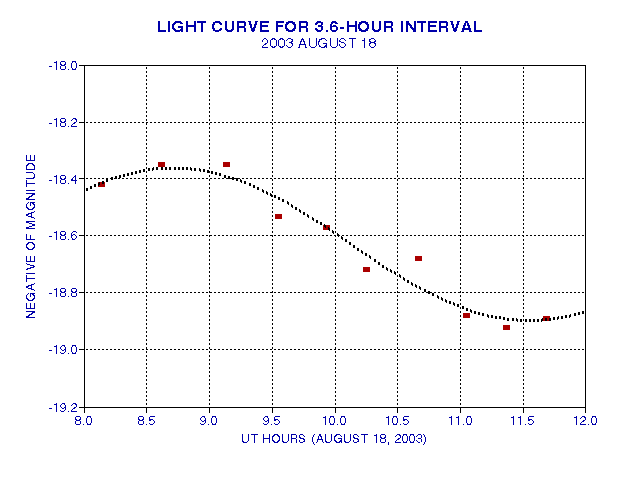
Figure 2003.07. Measured light curve and sinusoidal fit for the
10 measurements of August 18, 2003. The best fitting sinusoid has
a period of 5.68 hours, with an amplitude of 0.268 magntiude (half of peak-to-peak).
This implies that the rotation period is 11.36 hours. The standard
error uncertainty of the measurements based on their comparison with
the fitted sinusoid (4 degrees of freedom) is 0.057 magnitude.
It should be noted that a rotating body will have two maxima and two minima for each rotation. Thus, the sine wave period of 5.68 hours for this data implies a rotation period that is twice as long, or 11.36 hours.
Many caveats are appropriate here. First, asteroid light curves are usually more complex than a simple sinusoid. A detailed rotation light curve can have a short-period sinusoidal component superimposed upon a longer period variation. It is obvious that any rotation light curve can be decomposed into a series of Fourrier sinusoidal components with multiples of frequencies that go to large values (set by the shortest observing interval). The present data set is merely a demonstration of progress in observing, and a demonstration of a procedure for analyzing the data.
A second caveat is that the observations were unfiltered, which means that extinction effects are present. However, the entire data set was taken when the asteroid was rising and undergoing a monotonic decrease in air mass. There were no apparent cirrus clouds, and even if there were the magnitudes would be unaffected to first order because all asteroid brightnesses were measured from ratios to a standard star in each image, and both stars should be affected by the same amount (unless the colors of the star and asteroid differed greatly).
It will be noted that the average magnitude of the asteroid is 18.6. This is 0.8 magnitudes fainter than the JPL Ephemeris prediction, and 0.6 magnitudes fainter than a short observation 20 days earlier (during which time the asteroid should have brightened by 0.2 magnitude). It is possible for a non-spherical asteroid's distance-normalized magnitude to vary with time due to varying orientation of the rotation vector. Not only is it possible for an asteroid's average brightness to vary differently than a spherical shape model would predict, but an asteroid can even have different light curves for different viewing geometries. These variations of variations can enable an asteroid's shape and rotation vector to be inferred by a complicated modeling procedure.
The above light curve implies that the peak-to-peak brightness variation is 0.54 magnitude, or that the minimum brightness is 61% of the maximum. This is large, but not impossible. An asteroid with a two-sphere shape will exhibit a 2-fold change in brightness if the rotation vector is perpendicular to the observing direction (this assumes the rotation vector is perpendicular to the line joining the two spheres). Albedo variations across the asteroid can produce additional brightness variations, and in theory they can add to those produced by rotation.
It is clear from the foregoing that asteroid rotations light curves, made at times of different viewing geometries (different months, etc), can provide information on an asteroid's rotation period, rotation vector, and albedo variation. This makes the project of monitoring asteroid light curves interesting, and fun!
2003.09.04 Observations
Unfiltered exposures made on 2003.09.04Z illustrate the difficulty of monitoring the brightness of this asteroid when it is fainter than expected.

Figure 2003.08. Average of 21 60-second exposures, unfiltered,
on 2003.09.04Z. The oval is Asteroid 12753 Povenmire, showing a
track during the 80-minute observing session. Magnitudes for two
stars are shown. FOV = 7.1x5.9 'arc and FWHM = 3.9 "arc.
In this image the asteroid appears fainter than a star of magnitude 19.6, but this is due to the asteroid's movement which spreads out it's light when the star field is used to align the 4 images that were averaged.
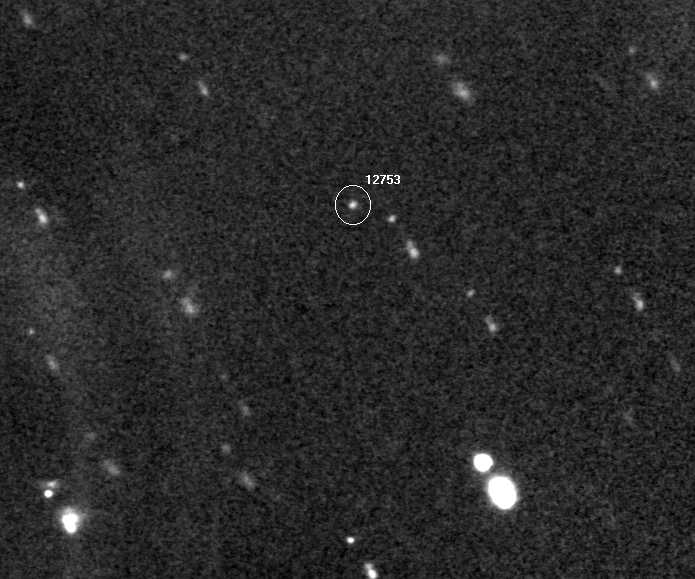
Figure 2003.09. Average of the same 4 images as above, except aligning
them so that the asteroid is at the same location.
When the images are aligned to the asteroid's position the stars are spread out and the asteroid appears brighter. Magnitude estimates from the four frames that compose this set of observations are 18.7, 18.5, 18.5 and 18.5. The average brightness is ~1.1 magnitudes fainter than JPL Ephemeris predictions (17.4). In other words, the asteroid appears to have a brightness that is 36% of the expected value.
2003.09.26 Observations of Asteroid Colors
During the evening of September 25, 2003 I observed Asteroid 12753 for 2.5 hours with photometric filters BVRI and C (where C stands for "clear"). The hardware configuration consisted of my new "standard": CGE-1400, JMI Smart Focuser, Celestron focal reducer (meant for f/7 with a f/11 SCT), SBIG AO-7 image stabilizer, SBIG CFW-8 color filter wheel, and SBIG ST-8XE CCD. Flat fields were taken with each filter during sunset.
Because the asteroid is fainter than predicted, and because "atmospheric seeing" at my site has been worse than average lately, I chose 2x2 binning. Each pixel intercepts a small square on the sky with dimensions 1.8 x 1.8 "arc. Nyquist sampling requirements are met whenever the "seeing" FWHM > 3.6 "arc, which it was on this night. Using a 2x binning increases sensitivity for faint point sources by a factor root-2, provided the Nyquist sampling requirement is met. All integration times were 60 seconds, and groups of 8 light and 2 dark frames (same exposure) were made at least once for each filter setting.
The goal for these observations is twofold: 1) determine the "shape" of the asteroid spectrum using BVRI filters, and 2) determine the absolute values of the asteroid's brightness at the BVRI bandpasses for a specific epoch. The first goal is the easier one.
It is difficult to measure an object's magnitude at many filter colors when the images do not contain standard stars with well-measured BVRI magnitudes. Three approaches come to mind: 1) performing all sky photometry, which is a way of transferring magnitudes of well-calibrated stars in one part of the sky to the field of stars in the image of interest, 2) using USNO A2.0 B and R magnitudes for stars in the image field as starting points for performing a statistical determination of magnitudes at other colors, and 3) starting with a large number of V-magnitudes for stars in the image field whose average magnitude might be OK but whose individual magnitudes are likely to exhibit large errors (of order ~0.3 magnitude), and determining statistical magnitudes for the other colors.
A detailed discussion of these three methods can be found at Chart creation with photometric sequence and will not be repeated here. It was found that Method #1 is probably feasible but prone to such large errors that Method #2, which involves only slightly more work, is a far superior procedure.
Using Method #2 it the following magnitudes for the asteroid were determined:
Asteroid
Mb < 18.2
Asteroid Mv = 18.50 +/- 0.11 (SEstoch) +/- 0.11 (SEcal) +/- 0.16 (accuracy)
Asteroid Mr = 17.16 +/- 0.05 (SEstoch) +/- 0.07 (SEcal) +/- 0.09 (accuracy)
Asteroid Mi = 17.49 +/- 0.02 (SEstoch) +/- 0.06 (SEcal) +/- 0.06 (accuracy)
Asteroid
V-R = +1.34 +/- 0.12 (SEstoch) +/- 0.13 (SEcal) +/- 0.18 (accuracy)
Asteroid R-I = +0.33 +/- 0.05 (SEstoch) +/- 0.09 (SEcal) +/- 0.10 (accuracy)
To understand whether or not these two color ratios are unusual (for stars) we must consider histograms of V-R and R-I for typical stars. These are shown in the next two figures, which are based on the famous set of Landolt calibration stars.
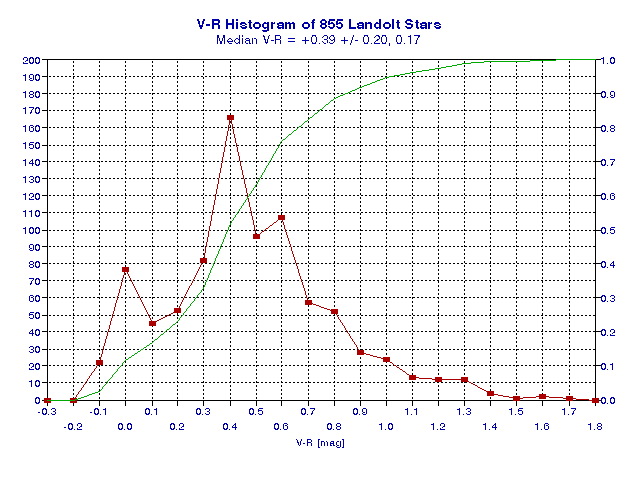
Figure 2003.10. Histogram of V-R for all Landolt stars (red).
The "integral to value" trace (green) shows that the median V-R is +0.39.
Half of all Landolt stars have V-R between the ranges +0.19 and +0.56
as indicated by the 25th and 75th percentiles.
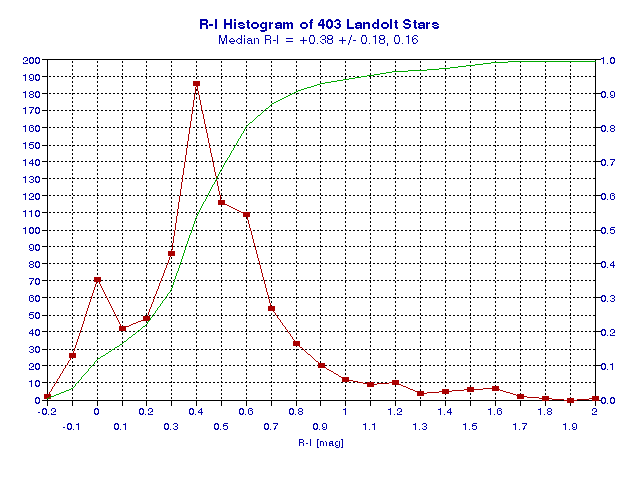
Figure 2003.11. Histogram of R-I for all Landolt stars (red). The
"integral to value" trace (green) shows that the median R-I is +0.38.
Half of all Landolt stars have R-I between the ranges +0.22 and +0.55
as indicated by the 25th and 75th percentiles.
The asteroid's R-I is typical for stars, as can be seen by referring to Fig. 13. However, the asteroid's V-R is unusual. Referring to Fig. 12 it can be seen from the green trace that only 1% of stars are as red as the asteroid in the VR spectral region.
There's a better way of comparing the asteroid's spectrum to that of stars, and that's to create a plot of V-R versus R-I and place the asteroid as well as the stars in the Landolt catalog in such a graph. This is done in the next figure.
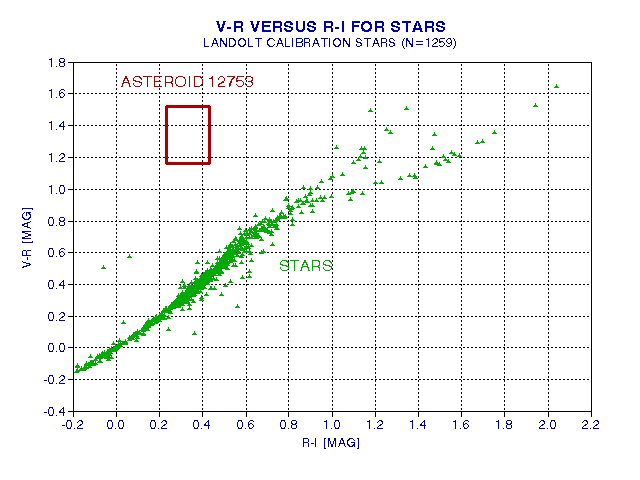
Figure 2003.12. Relationship between V-R and R-I for all stars in the Landolt catalog (green symbols) and for Asteroid 12753 Povenmire (red box). The asteroid box covers and area defined by the accuracy of the magnitude measurements.
Figure 14 shows that the asteroid is unlike all 1259 stars in the Landolt catalog. Since the sun is a typical star with color indices that will be place it among the green symbols on this graph, the only explanation for the asteroid being different is that it has an albedo spectrum that varies throughout the VRI region.
The BVRI filter spectral passbands are summarized in the next graph.
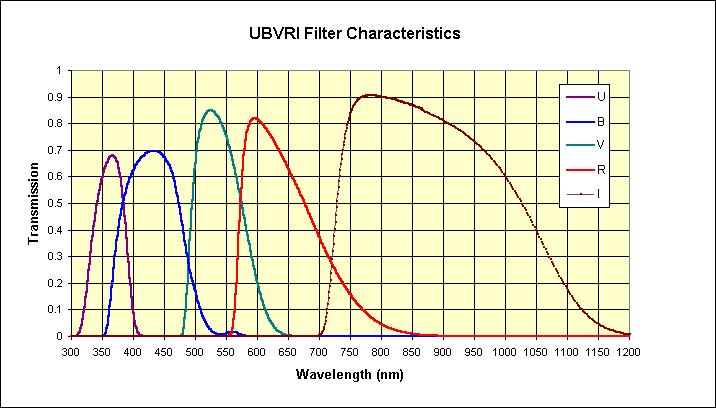
Figure 2003.13. Spectral response for BVRI filters.
The asteroid's R-I of +0.33 is typical for stars, so it's albedo must be approximately the same throughout the ~600 to 900 nm spectral region. However, because the asteroid's V-R is +1.34, the V magnitude must be high (faint) with respect to R, implying that the albedo decreases dramatically in going to shorter wavelengths from ~600 to ~500 nm. The anomaly is 1.0 +/- 0.20 magnitudes, corresponding to an intensity ratio of 2.5 +/- 0.5. This in turn implies that the asteroid's albedo at ~500 nm is only 40 +/- 8 % of its value at ~600 nm.
The analysis in the previous paragraph assumed asteroid's albedo between ~600 nm and ~900 nm is constant. This assumption is unecessary for computing the asteroid's albedo spectrum, since we know the sun's color. The sun and asteroid colors are compared in the following table.
Table I
Sun and Asteroid Colors
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The color differences between the asteroid and sun can be related to the asteroid's albedo. Between R and I passbands there is essentially no difference in asteroid albedo. But in going from R to V the asteroid's albedo drops 0.97 +/- 0.18 magnitude. In other words, the asteroid's albedo at V is only 40 +/- 8 % of its albedo at R. The asteroid's albedo drops this much somewhere in the 500 to 600 nm region (referring to Fig. 15).
If, for example, the asteroid's albedo at 650 nm were ~15%, at 530 nm it would be 6 +/- 1% according to the measurements reported here.
The following figures illustrates a possible albedo spectrum for the asteroid.
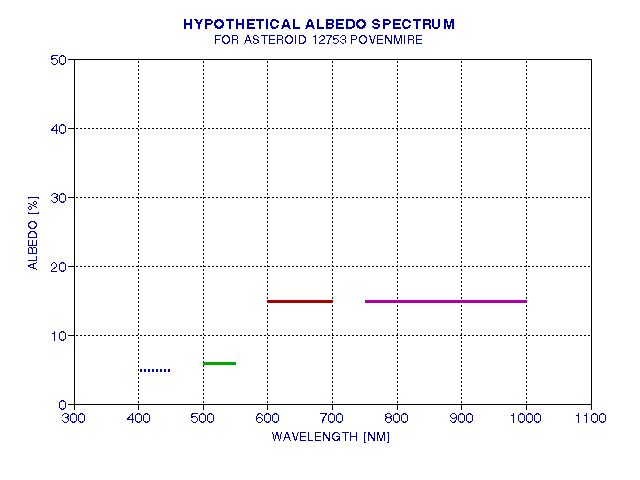
Figure 2003.14. Hypothetical albedo spectrum for the asteroid that
is compatible with the measurements reported here.
How reasonable is this spectrum? The next figure shows 4 asteroid spectra taken by the professionals.
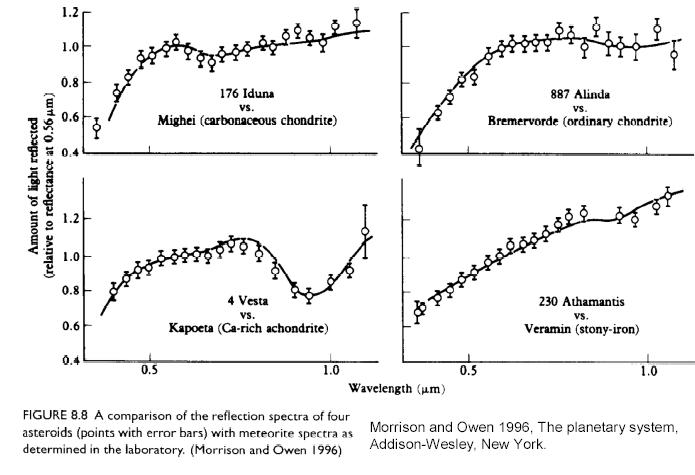
Figure 2003.15. Albedo spectrum for 4 asteroids, showing agreement
with carefull chosen meteorite albedo spectrae. From the internet:
http://www.solar-system-school.de/lectures/jockers/part2.pdf
This figure shows that asteroid albedos commonly decrease at short wavelengths, and a steep drop shortward of ~500 nm is common.
Observations of 2003.10.01 of Light Curve Using Infrared Filter
I have concluded that an "all-sky photometry" calibration on any clear night is better than a photometry calibration using POSS B and R magnitudes and conversion equations for getting V and I. This observing session was my first experience with all-sky photometry, and it was very successful. First, consider the distribution of Landolt stars in the region of 12753's motion during the 2003 opposition, shown in the next figure.
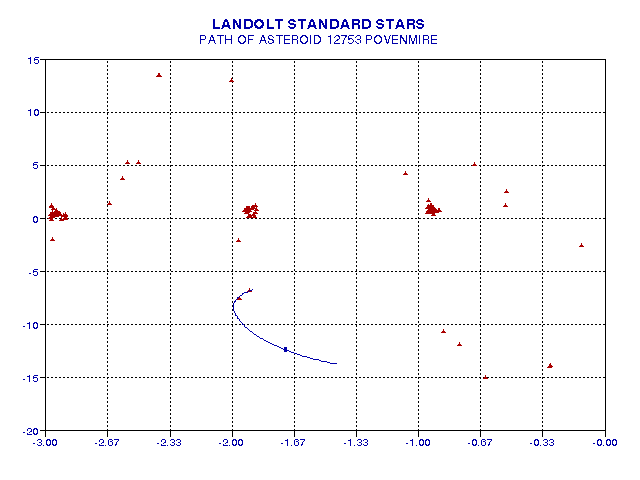
Figure 2003.16. Map of Landolt stars in the region of Asteroid
12753, whose path for Aug 1 through October 20 is shown (bue trace).
This figure shows that Asteroid 12753 passed very close to two Landolt stars in August, 2003. Four other Landolt stars precede the asteroid in their motion through local hour angle, LHA, at essentially the same declination. These stars are especially useful for calibrating the asteroid's magntidues since they can be observed and then 1 hour later the asteroid passes through the same LHA at the same air mass. The left-most of these stars was used to calibrate 12753's infrared magnitude during the October 1 (UT) observing session.
I transferred the I-magnitude from this Landolt star to a bright star in the CCD FOV that was centered on the asteroid's position. I observed the Landolt star later in the evening, when it was on the meridian (lowest air mass) just to see if I could assess the effect of greater extinction on the earlier measurement. Indeed, it had brightened, but only 0.12 magnitudes, or 11.7%. Air mass changed from 1.55 to 1.44, but if this were responsible for the brightening then an unreasonable 1.7 mag/air mass would have to be invoked. The more likely interpretation is that the atmosphere above me underwent an increase in transparency during the 2.5-hour interval, which requires a transparency change of 11.7% over a 2.5-hour interval. More on this later, but first let's just proceed with the innocent assumption that the atmosphere had zero extinction the whole time, and see what we find for the asteroid light curve. This is shown in the next figure.
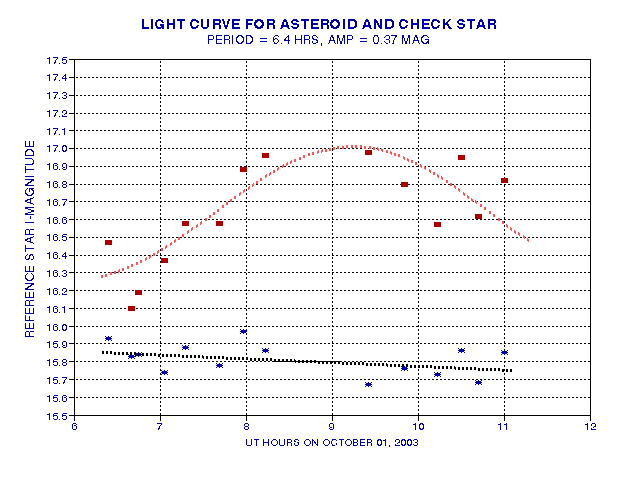
Figure 2003.17. Infrared magnitude of asteroid 12753 (red) and
a nearby "check star" (blue) during the 5-hour observing period of 2003 October
1 UT. These measurements assume that the atmopshere is transparent.
The least squares solution for a sinusoidal fit to the asteroid's magnitude
has a period of 6.4 hours and an amplitude of 0.37 magnitude (i.e., peak-to-peak
variation of 0.72 magnitude).
The rotation period that best fits this night's data (6.4 hours) is compatible with the period determined from the August 18 unfiltered measurements (5.7 hours). The best fitting amplitude (0.37 magnitude) also is compatible with the August 18 amplitude (0.27 magnitude). The present sinusoid fit has a greater uncertainty than for the August 18 data because an infrared filter was used in place of a clear filter.
But wait, the above figure assumed there was no atmosphere and my CCD had perfectly stable response during the entire 5-hour observing period. The CCD chip was temperature stabilized by a TEC, so the assumption of a stable CCD response might be OK. However, the atmopshere is likely to have changed since cirrus clouds were observed at the end of the observing period (which caused me to suspend observations). Notice that the check star's magnitudes change in a related way with the asteroid's magnitudes. Fortunately, I have two check stars, and the other one is much brighter than the one shown in the figure. The next figure shows how the bright check star's magnitude varied during the observing period.
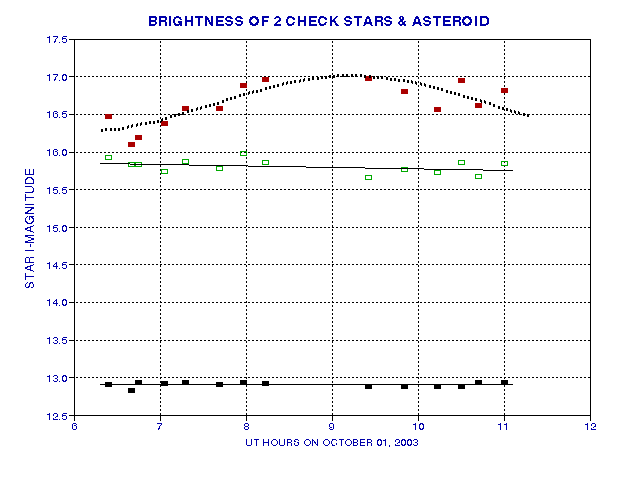
Figure 2003.18. Magnitudes of bright check star (black), a faint
check star (green) and the asteroid (red).
This figure shows two important things: 1) fainter stars exhibit more "noise" (no surprise), but 2) a faint check star does not exhibit the variations shown by the asteroid. This latter point gives confidence that the asteroid variations are real, and not an artifact of my data analysis. The first point suggests that if any corrections for atmospheric extinction changes are to be applied they should be based on the bright check star (and not the faint check star). Both check stars have served a useful purpose.
The next figure shows the faint check star and asteroid magnitudes after correction by the bright check star.
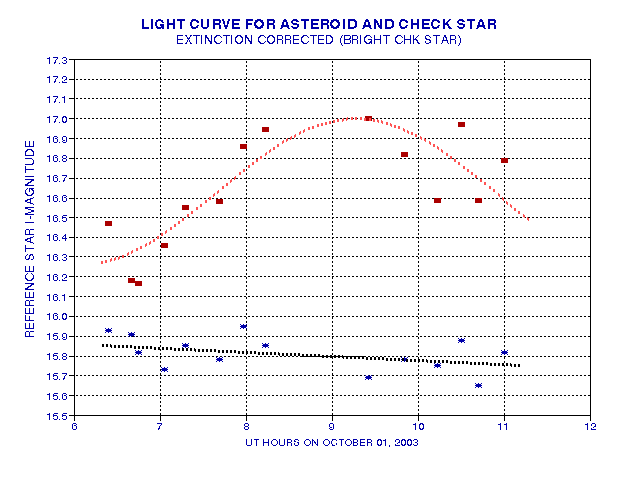
Figure 2003.19. Same as Fig. 17 except that the faint check star
and asteroid magnitudes have been corrected for atmopsheric extinction
changes using the bright check star. Best ftting sinusoid for the
asteroid has the following parameters: Avg Mi = 16.63 mag, amplitude
= 0.37 mag, period = 6.45 hours (rotation period = 12.9 hours), phase =
7.66 hours. RMS differences of check star and asteroid from a straight
line and the sinusoidal fit are 0.086 and 0.266 mag.
There's little change between Fig. 17 and 19, implying that the atmosphere's extinction was stable and did not degrade the faint star and asteroid brightness measurements using a simple all-sky photometry procedure. There's a greater RMS difference of the asteroid with respect to its sinusoid curve than the RMS difference of the faint check star with respect to its straight line fit. Most of this difference in RMS can be attributed to the fact that the asteroid is fainter, 0.83 magnitudes fainter on average, than the faint check star.
The greatest significance of these measurements is a validation of the idea that unfiltered measurements can be counted on to give the same results as those with the infrared filter. This is an important finding from my observational perspective, because I would much prefer to observe a faint object unfiltered. There's an approximate 4-fold improvement in "information rate" for unfiltered (or "clear" filter) observations compared with infrared filter observations. The reason for using an infrared filter to verify the quality of unfiltered observations is based on the fact that atmospheric extinction is very small at infrared, whereas it increases greatly in going to blue. Since the asteroid is essentially devoid of blue light, and is faint in visible, the unfiltered observation is almost equivalent to using a filter that passes both the red and infrared. This about doubles the signal level, which then leads to a 4-fold improvement in achieving a given percentage precision per unit of observing hour. I plan on conducting all future observations for establishing a light curve with the CLR filter (unfiltered).
Observations of 2003.10.04: Light Curve Using Clear Filter
Given that the asteroid is very red, and red stars experience small levels of extinction, I have adopted the unfiltered configuration for determining the asteroid's light curve. (Use of a "clear" filter is equivalent to unfiltered, the only difference being the focus setting.) On the night of October 3 (October 4 UT) I observed the asteroid from 4.0 UT to 9.3 UT, with observing cycles that consisted of 8 1-minute exposures and 3 dark 1-minute exposures. Analysis included two check stars, having magnitudes of 11.8 and 17.0 (approximately). Air mass ranged from 3.5 to 1.4, so it was possible to construct extinction curves. The bright and faint check stars had extinction values of 0.163 mag/air mass and 0.148 mag/air mass. Apparently the faint check star was redder than the bright one. After transit, that required a "meridian flip," both check stars were fainter; the bright star lost ~0.09 mag and the faint check star lost ~0.16 mag. I don't understand this, and can only blame it on the CCD being orientation sensitive (as if the TEC cooler was less effective after transit, perhaps due to gravity effect on air circulation). Since the faint reference star was closer to the asteroid than the bright star, and since it more closely resembled the asteroid in color, I chose to adopt the faint check star for corrections to the asteroid magntiudes due to both effects: extinction and CCD response. The next figure shows the raw magnitude estimates of the faint check star and asteroid before any corrections.
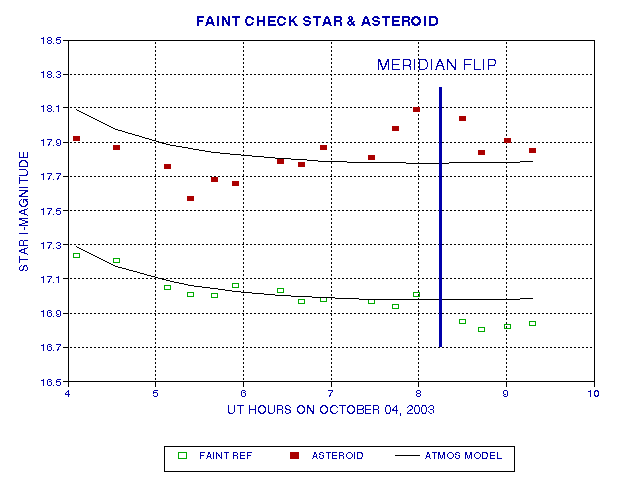
Figure 2003.20. Raw photometric magnitudes for the faint check
star (green) and asteroid (red) . Transit at 8.1 hours UT requried
a "meridian flip." Traces are used to show the atmospheric extinction
solution for the faint star's "pre-meridian flip" data (which is almost
identical to the solution for the bright check star).
The next figure shows the asteroid magnitudes after corrections that were based on the faint check star.
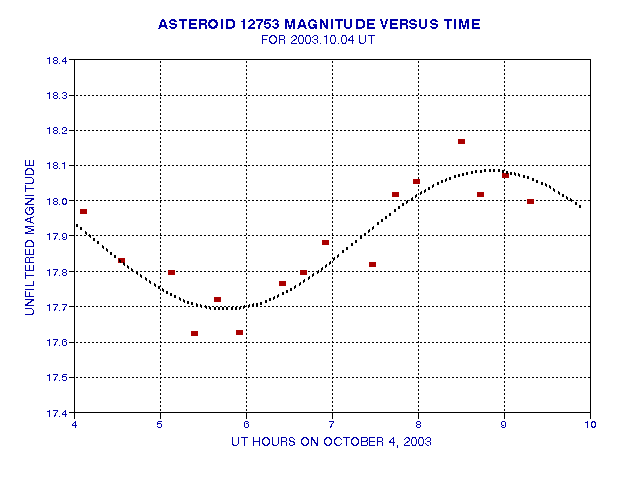
Figure 2003.21. Corrected magnitudes for the asteroid (corrections
based on the faint check star) versus time for October 4, 2003.
The least squares fit sinusoid has the following parameters: Period
= 6.13 hours (rotation period = 12.26 hours), amplitude = 0.196 magnitudes,
phase = 7.30 UT hours, 2003.10.04. The RMS deviation of the data from the
sinuoid fit is 0.065 magnitudes.
This result bothers me! It's a good fit, almost as good as could be expected from SNR considerations. However, minimum brightness ooccurs at 8.9 hours UT, 0.7 hours after transit, and this is similar to the result of 3 days earlier. The October 3 light curve has a minimum brightness at 9.2 hours UT, also 0.7 hours after transit. My first light curve, August 18, had a minimum brightness at 11.5 hours UT, which is exactly at transit. As an observationalist, I must wonder if there's a flaw in my observing technique that produces a minimum brightness at or slightly after transit for a red star.
If these light curves are taken at face value, the simplest interpretation of them is that the asteroid is rotating with a period very close to 12 hours. With the asteroid making 2 rotations per day, it will present approximately the same light curve every night. This would be a disconcerting situation from an observational standpoint. Nobody should believe a light curve that is correlated with transit!
Observations of 2003.10.06: Light Curve Using Red Filter
Observations were made with a red filter during a 5-hour interval on 2003 October 6, UT (evening of October 5). Although the red filter affords a lower SNR, I continue to feel the need to verify that the filtered and unfiltered measurements produce the same result. The extinction for this night was 0.15 magnitudes per air mass, and the air mass ranged from 2.04 to 1.40 at transit, then to 1.65 for the last observation. I processed the data slightly differently this time, because I wanted to achieve a good quality R-magitude for the asteroid using all-sky photometry. I first observed a Landolt star that preceded the asteroid by ~50 minutes in its air mass versus time progression. After the Landolt star I observed the asteroid and nearby stars until after it passed through the same air mass as the Landolt star (m=2.4). This allowed me to transfer the magnitude scale established by the Landolt star to the asteroid. The 5-hour average magnitude of the asteroid is Mr = 17.01 +/- 0.02.
The light curve for the asteroid was totally discrepant with the expected light curve. This was a clue that using the previous set of data I chose the wrong null in the periodic pattern of RMS off fit versus hypothesized period. These nulls occur at intervals of 0.125 hours, so I tried the periods that produced the neighboring nulls in the previous period solution exercise. The next lower period produced a poor fit, but a longer period afforded a good fit. It is shown in the next section, and argues for a period of 12.784 hours.
Observations of 2003.11.01 and 11.02: Light Curve HyperStar Prime Focus and Clear Filter
Observations were made with at prime focus using the Starizona HyperStar corrector lens on November 1 and 2, 2003. A clear filter was used since the asteroid is getting fainter with increasing distance to Earth. The observions lasted 4.0 hours and 7.1 hours. Use of the HyperStar has several advantages and one disadvantage. All the advantages are related to the fact that the field of view (FOV) is large, being 72 x 48 "arc. This means that the same calibration star used for one night can be used on at least two other nights for an asteroid moving at the speed of 12753. When two nights are used with the same calibration star there is a relaxed requirement for observing length; either night, or both, can be short observing sessions. When no single star is available for calibrating two observing nights, then each night's observations is subject to an unknown magnitude offset when all observing nights are combined for an analysis of the asteroid's light curve. When an observing session lasts at least a half rotation, which is ~3.2 hours for 12753, then an appropriate average can be estimated, but even this is subject to uncertainty. With the HyperStar it is possible to transfer the value for one reference star to another that is in the same FOV. This can be done for observing nights that are as much as 5 nights apart (assuming the present asteroid motion). Thre are other advantage to useing the HyperStar, but they are not worth describing here.
The only disadvantage in using the HyperStar prime focus configuration is that the point-spread-function (PSF) is greater than for the Cassegrain configuration. Typically, the HypeStar PSF has a full-width-half-maximum (FWHM) of ~8 "arc (varies from 7 to 9 "arc, depending on tracking and exposure time). For the Cassegrain configuration the PSF had a FWHM of 3"arc (varies from 2.0 to 4.5 "arc, depending on atmospheric seeing). The problem with a large PSF is that nearby stars are more likely to be a problem when choosing values for the photometry aperture radius, gap width and reference annulus width. To minimize unwanted interference of nearby stars it is important to use as small a value for these three parameters as possible. And the smaller the PSF the smaller these parameters can be, and the better the photometry. The HyperStar has PSF values almost 3 times larger than for the Cassegrain configuration. Since the errors grow in proportion to the areas of the photometry fields, this means that the HyperStar will typically have errors due to this effect that are ~7 times greater than for Cassegrain.
The November 2 asteroid track in the sky went past at least 3 faint stars, and corrections were applied for two of them. This correction is reminescent of what radio astronomers do at long wavelengths (longer than 10 cm) when observing a planet, since at these wavelengths there is a background of radio sources that are detectable with typical radiometers. This situation is called "confusion" in radio astronomy, and a proper analysis requires that a separate set of observations be made at a later date (or earlier) in order to observe only the background sources to establish what levels must be subtracted from the planet observations. In the present case, where the asteroid moves several point-spread-function widths in a matter of hours, the entire correction procedure can be made using a single night's observations.
The following image shows the asteroid's motion during the November 1 4-hour observing period.

Figure 2003.22. Asteroid motion during the 4-hour observing period
of November 1, 2003. The brightest star has a magnitude of 13.44,
and the asteroid averages 17.63 magnitude.
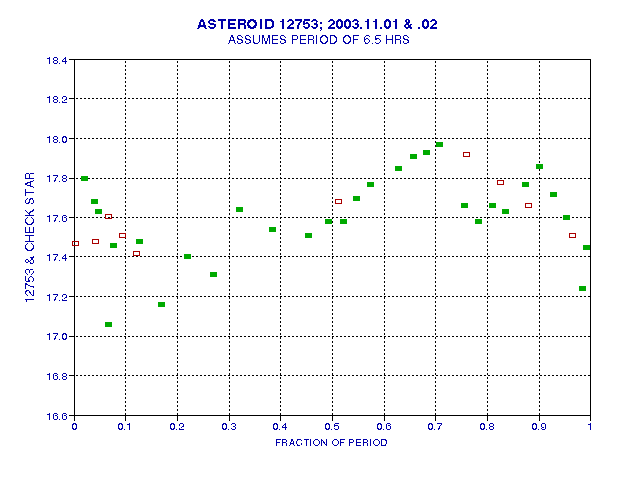
Figure 2003.23. Magnitude of asteroid for November 1 (red open
squares) and November 2 (green filled squares), versus a hypothetical rotation
period or 13 hours.
Some of the scatter of the green data in this plot are undoubtedly due to a "confusing star source" having a magnitude of 18.0 (almost the same as the asteroid's 17.6). The next figure shows the track of the asteroid and 6 "consfusing stars."
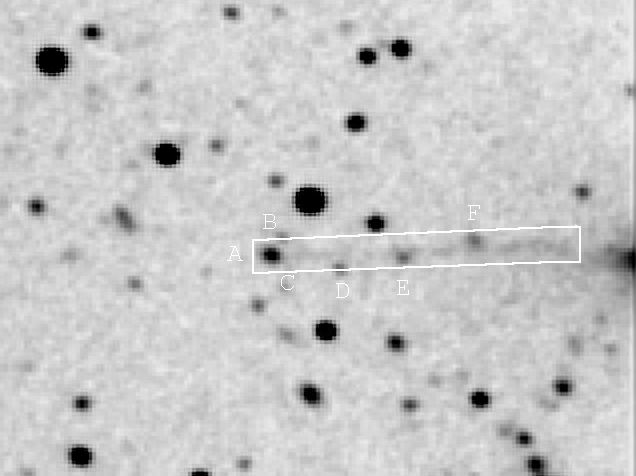
Figure 2003.24. Path of asteroid during the 7.1-hour 2003 November
2 observing period (within the rectangle) showing several "confusing stars."
Star "A" is the brightest confusing star, with a magnitude of 18.0.
Star "D" is 19.2, star "E" is 19.0 and star "F" is 18.8 mag. The
faintest stars in this image are magnitude 20.8. (Several faint
galaxies are present in this image.)
I averaged three measurements in the vicinity of the 18th magnitude "confusing star source" so that the resulting magnitude uncertainty will be comparable to the other measurements. The fainter the asteroid, the more important it is to correct for "confusing stars" or to choose observing dates when all confusing stars are faint. This is an example of what I like about a challenging observing project!
Observations of 2003.11.18:
I observed with the prime focus HyperStar configuration and a V-filter on November 18 UT. The 3-hour set of measurements were perfectly predicted by the previous data using a period of 12.8546 hours. The brightness variation consisted of a monotonic rise. A good absolute calibration was possible by using ASAS-3 V-magnitudes for the star field within the FOV. The average value is 17.8, which is 0.2 magnitudes fainter than for November 2 (my new standard date).
Combining All Light Curve Data for Establishing Period
Let's summarize the light curve sinusoidal fits to date:
YYYY.MM.DD FILTER OBS'G TIME PERIOD AMPLITUDE RMS Notes
2003.08.18
C 3.6 hrs 11.36 hrs
0.268 mag 0.057 mag Good quality data
2003.10.01 I 4.7 hrs
12.90 hrs 0.37 mag 0.266 mag
Moderatley good data
2003.10.04 C 5.3 hrs
12.26 hrs 0.196 mag 0.065 mag Good
quality data
2003.10.06 R 5.1 hrs
12.4 hrs 0.22 mag 0.11 mag
Poor SNR due to use of red filter
2003.11.01 C 4.0 hrs
?.? hrs ?.?? mag 0.10 mag
Good magnitude calibration star (V-mag)
2003.11.02 C 7.1 hrs
13.0 hrs 0..22 mag 0.14 mag
Confusing stars (correction attempted); used same cal star
2003.11.18 V 2.9 hrs
n/a
Good quality data, avg 17.8 mag
Each observing date contains phase information that must be compatible with every other date's observations. It is possible to improve the precision of a period by assuming all possible values for period, amplitude and phase and evaluating each hypothetical solution using RMS with respect to each hypothetical model prediction.
The proper procedure for this type of analysis is to assume a period, perform a least-squares solution for all other parameters (amplitude and phase are the principal ones), and record the resultant RMS. Then change the period by a small amount (that depends on the range of dates for which data exists), such as 0.001 hours, and perform another LS solution for amplitude and phase. Repeat the process untill all possible periods have been evaluated, and plot the RMS versus hypothetical period. The curve will have narrow "dips" at candidate period solutions, and one of these will have the deepest dip (i.e., smallest RMS).
This sounds like a lot of work, and indeed it is unless you have the appropriate parameter search program. I've written a program that does this comprehensive parameter search, and the next figure shows RMS versus hypothetical period with all non-period parameters LS solved.
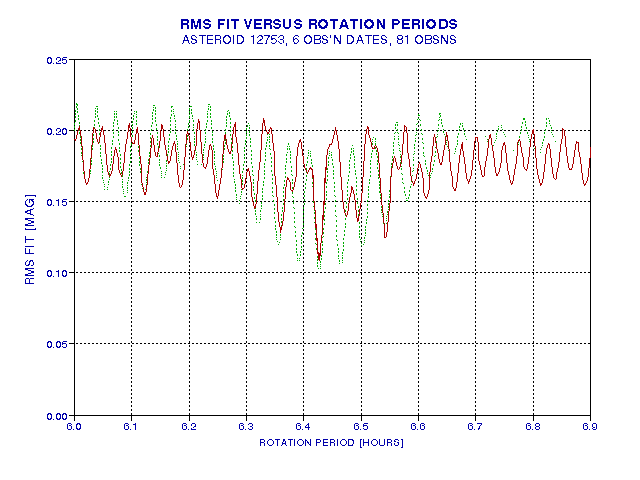
Figure 2003.24. RMS off of model fits where sinusoid period is
incremented in small steps and all other parameters are least-squares solved
for. The best solution is for a sinusoid period of 6.4267 hours (rotation
period of 12.8534 hours), amplitude = 0.210 magnitude, phase = October
4.550, yielding RMS = 0.109 magnitude. The dotted green trace is based
on all data before November, 2003.
The main message of this graph is that the rotation period is between 12.7 and 13.1 hours, with a most likely period of 12.8534 hours. The best solution is similar to two neighboring solutions, which differ by -0.144 hours and +0.226 hours. More observations are needed to rule-out the neighboring solutions.
Here's the current best solution model compared with measurements from the 6 observational dates.
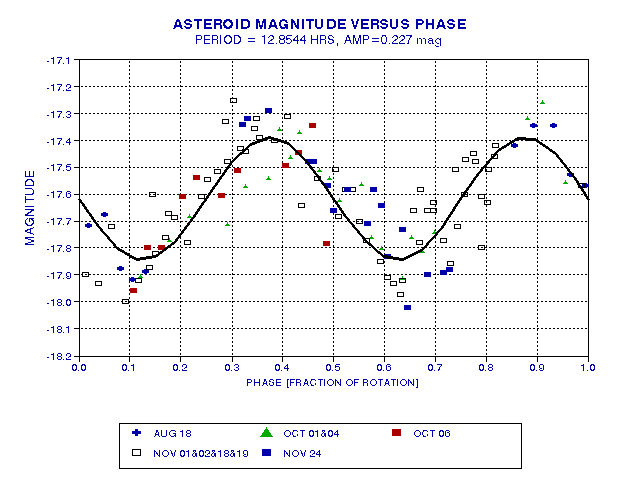
Figure 2003.25. Plot of all light curve data (to date) versus a
sinusoidal model having the following parameters: period = 12.8544
hours, amplitude = 0.227 magnitudes, phase = October 4.550 UT. RMS
residuals are 0.119 magnitude. Negative of magnitude is used so that
greater brightness is up. The magnitude scale agrees with red filter
measurements; the other filter observations have been adjusted so that
the average magnitudes agree.
There is accumulating evidence for a non-sinusoidal rotational light curve, and the following graph attempts to portray a hand-fit trace.
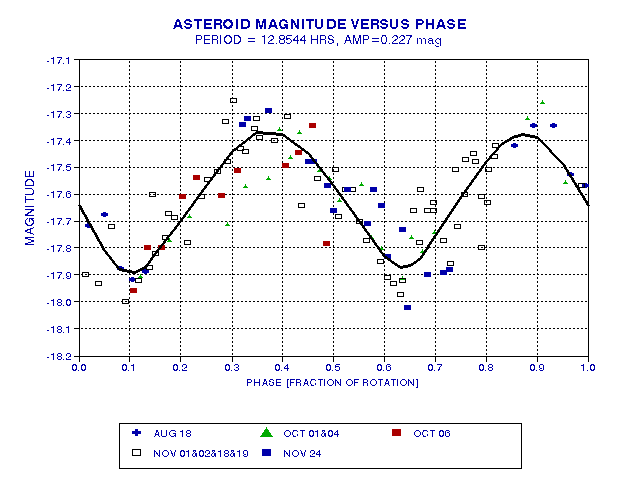
Figure 2003.26. Hand-fit trace of all data.
This hand-fit trace has more rounded maxima and "sharper" minima, which is tyical of rotating asteroids. The amplitude of variation can be explained by postulating that the asteroid has a "potato shape" with major to minor axis lengths >1.64. Other oppositions will be needed to improve this "solution."
Based on the excellent agreement of all data with the current best rotation period, I conclude that the asteroid has a period of 12.854 hours. [Wrong! It later turned out to be 17.56 hours.]
I could work on estimating a formal stochastic error for this period, using Bayesian concepts, but I intend to observe the asteroid more and derive much a more precise period.
The light curve's departure from a sinusoid is very interesting.
This is not unusual among asteroids, and the exact shape can be used
to constrain a solution for the shape of the asteroid. More on this
later.
![]()
What's Generally Known About Asteroids
For an informative set of viewgraphs on asteroids, go to http://www.solar-system-school.de/lectures/jockers/part2.pdf
Here are a few figures from that article:
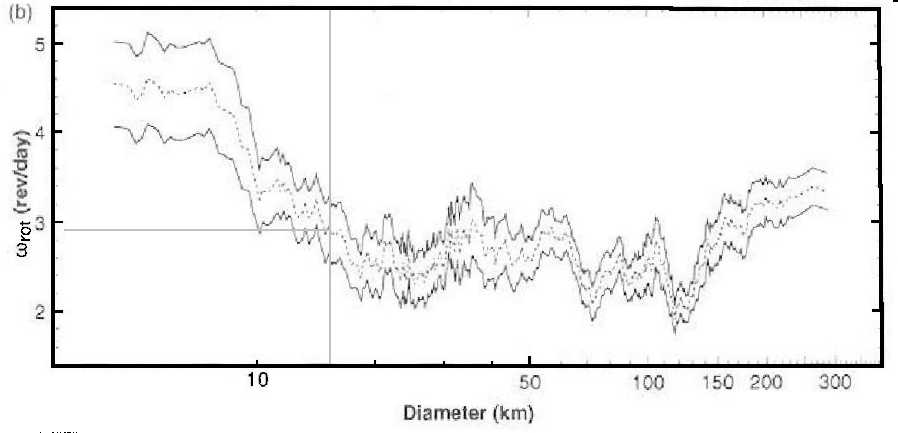
I've place a vertical line at the 16 km (10 mile) diameter x-axis location
in order to show that the most-likely rotation rate is 2.9 revolutions
per day (period of 8.2 hours) for an asteroid having the diameter attributred
to Asteroid 12753.
References
Scheirich, Petr, 2005, http://sajri.astronomy.cz/asteroidgroups/groups.htm
This site opened: July 19, 2003. Nothing on this web page is copyrighhted. Last Update: 2010.06.28