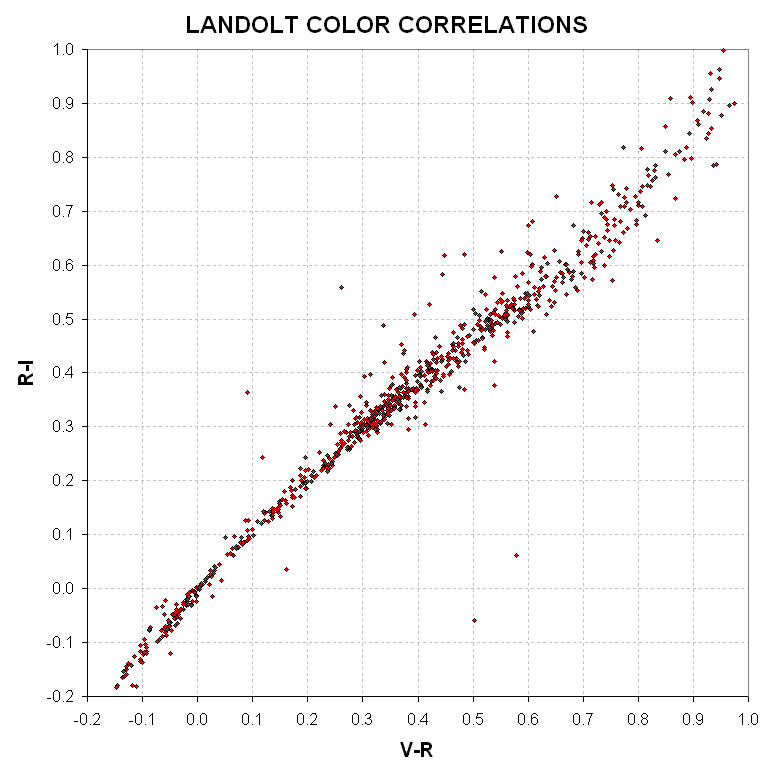
This web page describes a procedure for
calibrating an image using USNO-A2.0 B and R magnitudes for some of the
stars in that image. You'll have to download a list of information for
several stars within a specified distance of your region of interest
(ROI).
Step 1: "Plate Solve" the image. Use PinPoint to perform an astrometric solution for the image of interest. Inspect it and decide what part of it has the best stars for calibration purposes. The best stars will be bright but unsaturated and free of nearby interfering stars. Note the RA/Dec for the middle of this ROI.
Step 2: Download USNO-A2.0 B and R magnitudes for the ROI. Direct your browser to http://archive.eso.org/skycat/servers/usnoa and fill out the folowing fields: RA (HH:MM:SS), Dec (+DD MM SS), Radius (7), Bright Limit (8), Faint Limit (16), Sort Record (pull down menu), Number of ouput objects (100). After a couple seconds you'll see a display of 1-liners for up to 100 stars. Save this web page to a directory as a text file. The filename could be USNO_6622.TXT, for example.
Step 3: Import USNO-A2.0 information to Excel. View the file and note the order of data entried (i.e., number, ID, RA, Dec, R-mag, B-mag, distance from ROI, PA for this radial distance). Use Mixrosoft Windows Notepad to delete the header lines. Run Excel. Import USNO_6622.TXT to Excel (Alt-D, D, D, navigate to your directory, double-click the filename, check "Fixed Width", Next, verify column settings for data separation, Finish, OK).
Step 4: Convert USNO B and R magnitudes to Landolt-equivalent B, V and R. Note that the USNO-A2.0 data lists only R and B magnitudes. These are from readings of Palomar Observatory glass plates from up to 50 years ago. These R and B magnitudes, which I'll refer to as Ru and Bu, have to be converted to Landolt-equivalent B, V and R magnitudes. This can be done for the entire list of stars in the spreadsheet using the following conversion equations:
B = 1.097 * Bu - 1.216 Eqn 1
V = 1.064 * [ (5 * Ru + 3 * Bu) / 8 ] - 0.822 Eqn 2
R = 1.031 * Ru - 0.417 Eqn 3
These conversion equations are described as accurate for Bu and Ru magnitudes between 12 and 19.
Here's what your spreadsheet could look like:
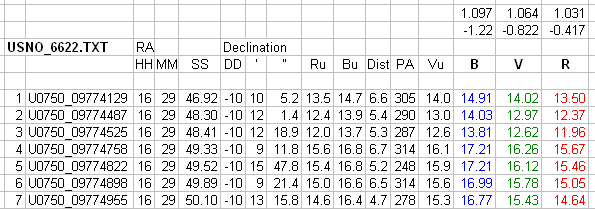
Figure 1. Data from the USNO-A2.0 site were imported to the upper-left cell containing a "1" and it filled columns as far as the one labelled "PA." The columns labelled Vu, B, V and R are calculated.
Step 5: Compile list of calibration stars.
Print your image so you can make notes on it. To do this first convert it to an "inverse" version so that most of the image is white. (With MaxIm DL this can be done using the following steps: adjust brightness and contrast to your liking, open the Screen Stretch window, click "+" on this window, drag the two pointers that are below the histogram to the opposite ends, further adjust the brightness and contrast so to get mostly white, do a Process/Stretch (linear, screen stretch, 8-bit, OK), save as a JPG image with a suitable filename change).
Circle the stars you want to use as "calibrators" and assign a sequence number to each one. Create a table in your reduction log with a line for each star. Record the RA/Dec for each of these stars (with MaxIm DL viewing this info is easy).
Scan the list of stars in the spreadsheet to identify each of your calibrator candidates. (It helps when their listed in order of RA, for example. (If they're not ordered this way consider creating such an ordering.) Record in your reduction log table the BVR magnitudes for each calibrator candidate star.
Step 6: Solve for the Zero Shift constant for this image. Let's begin by assuming that we chose only one star as a calibrator. Suppose this star had B = 13.26 and V = 12.23. Suppose further that we're working with a 60-second exposure image taken with a B-band filter. Assume we measure the flux from this star to be 14,550 counts (using a photometry aperture radius that we plan on using later to measure the target object, such as a faint asteroid). From previous calibrations of our telescope system (observing Landolt star fields) we know the following for B-band:
B-mag = Z - 2.5 * LOG10 ( S / g ) - Kb * m + 0.32 * C Eqn 4
where Z is a zero shift constant (~19.31 for my system), S is star flux [counts], g = exposure time [sec], Kb is B-band zenith extinction (~0.24 [mag/airmass] for my site), m is air mass, and C is star color. Star color is defined here to be:
C = 0.57 * ( B - V ) - 0.30 Eqn 5
Our star has C = +0.29. Since we're only calibrating one image it isn't necessary to use an accurate vlue for Zb or to calculate air mass m. In the spreadsheet illustration I'll simply use a nomal Z and a known air mass value. We can now evaluate Z because we have values for all other terms in Eqn 4. Rearranging terms, we have:
Z = B-mag + 2.5 * LOG10 ( S / g ) + Kb * m - 0.32 * C Eqn 6
Z = 13.26 + 2.5 * LOG10 ( 14550 / 60 ) + 0.24 * 1.41 - 0.32 * (+0.29) Eqn 7
Z = 19.47
If this were a good quality value for Z we could convert the flux for any other star in this image to B-mag. However, recall that the USNO magnitudes are quantized at the 0.1 mag level, and any single star is likely to be uncertain for a variety of other reasons (it could be a variable, there might have been a defect on the Palomar plate, etc). It has been estimated that the USNO catalog list of Ru magnitudes should be treated as exhibiting an uncertainty of ~0.26 magnitude (RMS). The Bu uncertainty is presumably similar. Therefore, with only a single star we can expect our evaluation of Z to exhibit an uncertainty of at least 0.26 mag. There could be an additional component of uncertainty associated with our star flux measurement. For the specific example treated here the star's flux was measured with SNR = 311, which corresponds to SE = 1/311 mag, which is negligible in relation to the USNO uncertainty.
If we used 4 calibrator stars we would reduce the USNO component of uncertainty by a factor 2 (assuming the errors for nearby stars are uncorrelated). After repeating the above procedure for 3 additional stars, using the same image in this case study example, we have a spreadsheet that looks like the following:
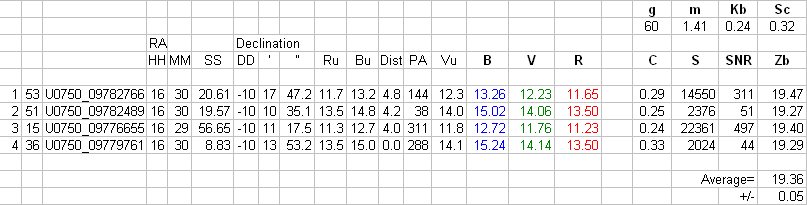
Figure 2. Four USNO stars are used to derive an average value for the zero shift constant for converting B-band star fluxes to B-mag.
For the 4 stars chosen there is a small internal scatter implying a small uncertainty for the average Z value (19.36 +/- 0.05 mag). There probably is a systematic error that all stars share, which is likely considering that they probably all were measured from the same Palomar plate. A more likely SE uncertainty for the average Z is 0.13 mag (although I've achieved 0.05 SE on several occasions while using ~8 USNO-A2.0 stars).
When using several USNO-A2.0 stars to establish a zero shift constant for an image it is advisable to median combine the several zero shift values instead of averaging. This minimizes the effects of star variability and image defects.
Step 7: Measure the target object's flux and convert to magnitude. Now that a zero shift value for B-band has been determined for this one B-filter image, it is possible to convert all other star fluxes to a B-mag using the following equation:
B-mag = 19.36 - 2.5 * LOG10 ( S / 60 ) - 0.24 * 1.41 + 0.32 * C Eqn 8
Miscelaneous Comments
Step 1: "Plate Solve" the image. Use PinPoint to perform an astrometric solution for the image of interest. Inspect it and decide what part of it has the best stars for calibration purposes. The best stars will be bright but unsaturated and free of nearby interfering stars. Note the RA/Dec for the middle of this ROI.
Step 2: Download USNO-A2.0 B and R magnitudes for the ROI. Direct your browser to http://archive.eso.org/skycat/servers/usnoa and fill out the folowing fields: RA (HH:MM:SS), Dec (+DD MM SS), Radius (7), Bright Limit (8), Faint Limit (16), Sort Record (pull down menu), Number of ouput objects (100). After a couple seconds you'll see a display of 1-liners for up to 100 stars. Save this web page to a directory as a text file. The filename could be USNO_6622.TXT, for example.
Step 3: Import USNO-A2.0 information to Excel. View the file and note the order of data entried (i.e., number, ID, RA, Dec, R-mag, B-mag, distance from ROI, PA for this radial distance). Use Mixrosoft Windows Notepad to delete the header lines. Run Excel. Import USNO_6622.TXT to Excel (Alt-D, D, D, navigate to your directory, double-click the filename, check "Fixed Width", Next, verify column settings for data separation, Finish, OK).
Step 4: Convert USNO B and R magnitudes to Landolt-equivalent B, V and R. Note that the USNO-A2.0 data lists only R and B magnitudes. These are from readings of Palomar Observatory glass plates from up to 50 years ago. These R and B magnitudes, which I'll refer to as Ru and Bu, have to be converted to Landolt-equivalent B, V and R magnitudes. This can be done for the entire list of stars in the spreadsheet using the following conversion equations:
B = 1.097 * Bu - 1.216 Eqn 1
V = 1.064 * [ (5 * Ru + 3 * Bu) / 8 ] - 0.822 Eqn 2
R = 1.031 * Ru - 0.417 Eqn 3
These conversion equations are described as accurate for Bu and Ru magnitudes between 12 and 19.
Here's what your spreadsheet could look like:

Figure 1. Data from the USNO-A2.0 site were imported to the upper-left cell containing a "1" and it filled columns as far as the one labelled "PA." The columns labelled Vu, B, V and R are calculated.
Step 5: Compile list of calibration stars.
Print your image so you can make notes on it. To do this first convert it to an "inverse" version so that most of the image is white. (With MaxIm DL this can be done using the following steps: adjust brightness and contrast to your liking, open the Screen Stretch window, click "+" on this window, drag the two pointers that are below the histogram to the opposite ends, further adjust the brightness and contrast so to get mostly white, do a Process/Stretch (linear, screen stretch, 8-bit, OK), save as a JPG image with a suitable filename change).
Circle the stars you want to use as "calibrators" and assign a sequence number to each one. Create a table in your reduction log with a line for each star. Record the RA/Dec for each of these stars (with MaxIm DL viewing this info is easy).
Scan the list of stars in the spreadsheet to identify each of your calibrator candidates. (It helps when their listed in order of RA, for example. (If they're not ordered this way consider creating such an ordering.) Record in your reduction log table the BVR magnitudes for each calibrator candidate star.
Step 6: Solve for the Zero Shift constant for this image. Let's begin by assuming that we chose only one star as a calibrator. Suppose this star had B = 13.26 and V = 12.23. Suppose further that we're working with a 60-second exposure image taken with a B-band filter. Assume we measure the flux from this star to be 14,550 counts (using a photometry aperture radius that we plan on using later to measure the target object, such as a faint asteroid). From previous calibrations of our telescope system (observing Landolt star fields) we know the following for B-band:
B-mag = Z - 2.5 * LOG10 ( S / g ) - Kb * m + 0.32 * C Eqn 4
where Z is a zero shift constant (~19.31 for my system), S is star flux [counts], g = exposure time [sec], Kb is B-band zenith extinction (~0.24 [mag/airmass] for my site), m is air mass, and C is star color. Star color is defined here to be:
C = 0.57 * ( B - V ) - 0.30 Eqn 5
Our star has C = +0.29. Since we're only calibrating one image it isn't necessary to use an accurate vlue for Zb or to calculate air mass m. In the spreadsheet illustration I'll simply use a nomal Z and a known air mass value. We can now evaluate Z because we have values for all other terms in Eqn 4. Rearranging terms, we have:
Z = B-mag + 2.5 * LOG10 ( S / g ) + Kb * m - 0.32 * C Eqn 6
Z = 13.26 + 2.5 * LOG10 ( 14550 / 60 ) + 0.24 * 1.41 - 0.32 * (+0.29) Eqn 7
Z = 19.47
If this were a good quality value for Z we could convert the flux for any other star in this image to B-mag. However, recall that the USNO magnitudes are quantized at the 0.1 mag level, and any single star is likely to be uncertain for a variety of other reasons (it could be a variable, there might have been a defect on the Palomar plate, etc). It has been estimated that the USNO catalog list of Ru magnitudes should be treated as exhibiting an uncertainty of ~0.26 magnitude (RMS). The Bu uncertainty is presumably similar. Therefore, with only a single star we can expect our evaluation of Z to exhibit an uncertainty of at least 0.26 mag. There could be an additional component of uncertainty associated with our star flux measurement. For the specific example treated here the star's flux was measured with SNR = 311, which corresponds to SE = 1/311 mag, which is negligible in relation to the USNO uncertainty.
If we used 4 calibrator stars we would reduce the USNO component of uncertainty by a factor 2 (assuming the errors for nearby stars are uncorrelated). After repeating the above procedure for 3 additional stars, using the same image in this case study example, we have a spreadsheet that looks like the following:

Figure 2. Four USNO stars are used to derive an average value for the zero shift constant for converting B-band star fluxes to B-mag.
For the 4 stars chosen there is a small internal scatter implying a small uncertainty for the average Z value (19.36 +/- 0.05 mag). There probably is a systematic error that all stars share, which is likely considering that they probably all were measured from the same Palomar plate. A more likely SE uncertainty for the average Z is 0.13 mag (although I've achieved 0.05 SE on several occasions while using ~8 USNO-A2.0 stars).
When using several USNO-A2.0 stars to establish a zero shift constant for an image it is advisable to median combine the several zero shift values instead of averaging. This minimizes the effects of star variability and image defects.
Step 7: Measure the target object's flux and convert to magnitude. Now that a zero shift value for B-band has been determined for this one B-filter image, it is possible to convert all other star fluxes to a B-mag using the following equation:
B-mag = 19.36 - 2.5 * LOG10 ( S / 60 ) - 0.24 * 1.41 + 0.32 * C Eqn 8
Miscelaneous Comments