This web page documents my photometric sequence observations for the exoplanet IL Aqr (GL 876, GJ 876).
Star field overview and suggested reference stars
CLose Double Warning
All-Sky Photometry Observations of Landolt Stars
Miscellaneous Links
TransitSearch and AAVSO Collaboration
The AAVSO is interested in exoplanet observing projects, and the
upcoming exoplanet IL Aqr transit windows of 2004.10.21 and 22 will be
the first observing project that the AAVSO is coordinating with the
TransitSearch group. Web pages for TransitSearch start at http://www.transitsearch.org/links.htm
and the AAVSO web page for the IL Aqr project is at http://www.aavso.org/news/ilaqr.shtml
Photometric Sequence (Suggested Reference Stars)
The exoplanet system IL Aqr is located at 22:53:17.03, -14:15:52.6
(equinox 2000.0, according to my UCAC 2.0 astrometry, with a RMS
residual of 0.2 "arc). The following image shows the stars in the IL
Aqr region. Here are my suggested "referecne star" magnitudes.
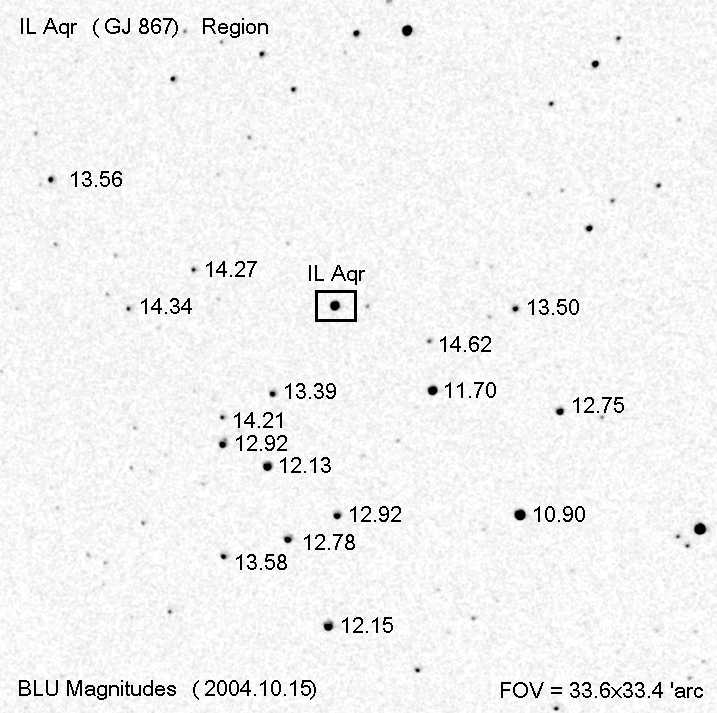
Figure 1. Suggested reference star magnitudes for B-band filters.

Figure 2. V-magnitudes. FOV = 35.8 x 38.3 'arc,
north up, east left. SE uncertainty is 0.05 magnitude.
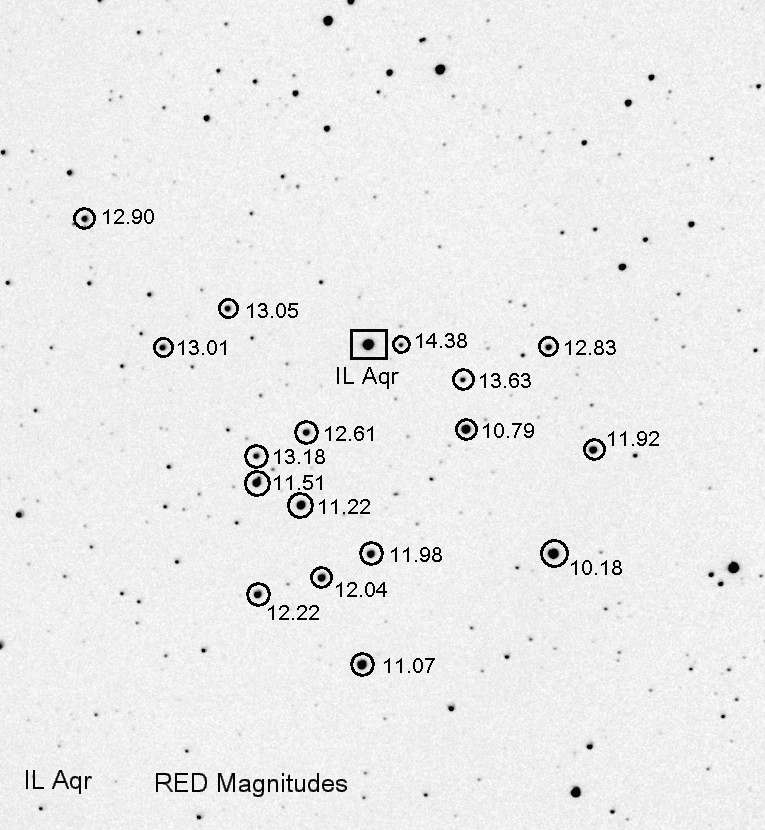
Figure 3. R-magnitudes. FOV = 35.8 x 38.3 'arc, north up, east left. SE uncertainty is 0.08 magnitude.
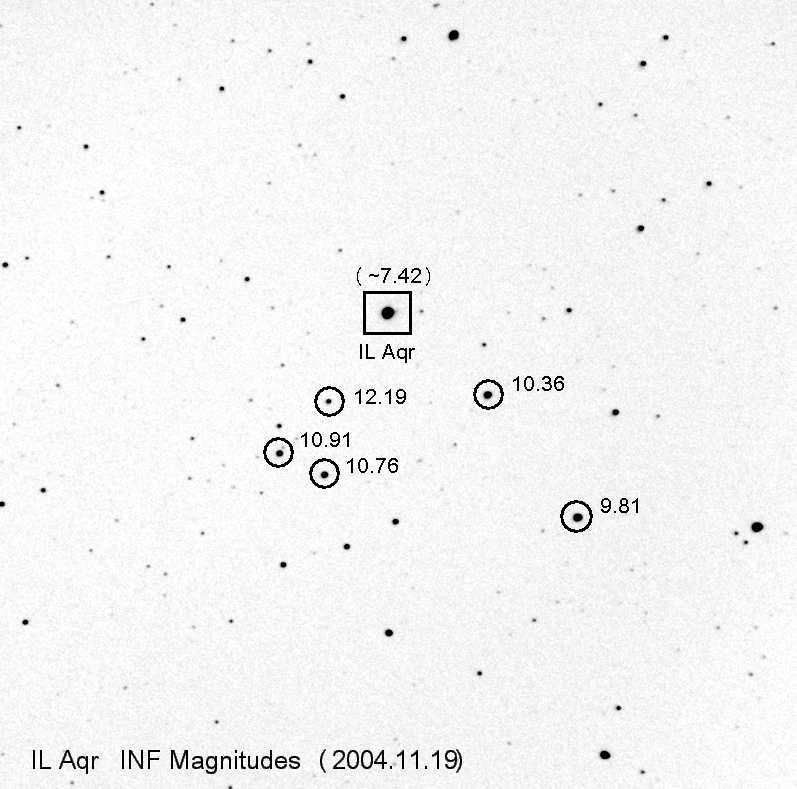
Figure 4. I-magnitudes (INF = I-band). FOV = 36 x 38 'arc, north up, east left. SE uncertainty is 0.06 magnitude.
None of the magnitudes in the above 4 images have been "endorsed" by the AAVSO; they are my determinations from all-sky observations conducted 2004.10.15.
Aaron Price (AAVSO) has suggested using reference star with a
V-magnitude of 11.93 since it is very red, like IL Aqr. This star,
hereafter referred to as *119, has a problem, however. It's a double,
with the fainter star ~17 "arc to the NNE (pa = 327 degrees), as shown
in a low resolution image below. The faint star is 3.0 magnitudes
fainter than *119
using a V-band filter.
My photometry of *119 excluded the nearby faint
star by employing a technique that would horrify most observers; I used
a pixel editing feature to "remove" the faint star from the image
(using a copy of the original for the horrific deed), then performed
the photometry using that edited image. (I'm practised in this from my
faint asteroid light curve work, where an asteroid is always going near
faint stars during the course of an evenning's observing.) I didn't
have the option of changing the "aperture radius/gap annulus width/sky
reference annulus width" settings because doing that would render my
equation predicted magnitude (described in the next paragraph) unusable
for those changed settings. The way I recommend handling this faint
interfering star for exoplanet monitoring is to set the signal aperture
so that the faint star is entirely within or entirely outside the
signal aperture (and not withni the sky reference annulus). The effect
of completetly including the faint star within the signal aperture is
to merely introduce a slight offset in the exoplanet magnitudes, and
provided all images are reduced with the same aperture settings this
will not cause changes in the exoplanet light curve.

Figure 5. This is the preferred way to set aperture
radius, gap width and sky reference annulus so that the neaerby
interfering star does not affect the measured intensity of reference
star 119. FOV = 6.0 x
5.8 'arc, north up, east left (crop of a 72 x 48 'arc image).
All-Sky Photometry Using
Landolt Stars
Two nights were used to establish the photometric sequence presented
above. I will describe obserations for the second night since it
consisted of many more Landolt stars, a greater air mass range and an
equation for converting intensity to magnitude that included an
additional term.
I employ a novel scheme for
converting measured star intensity to magnitude (described at http://brucegary.net/AllSky/x.htm).
It is based on the idea that the intensity of a star in a CCD image is
proportional to the star's brightness, to first order. In addition, it
is assumed that allowance must be made for extinction effects, an
instrumental response to stars of various colors, and a term that
allows for the fact that the broad-band spectrum of a star is affected
by total extinction (i.e., zenith extinction times air mass). It is
just as intuitively obvious that a reverse calculation should be
possible, namely that brightness is proportional to star intensity and
all factors that affect apparent brightness. Linear dependencies are
assumed, so the desired equation for deriving brightness from measured
intensity, air mass, extinction, an instruemntal response term and a
product term should look something like the following:
Magnitude = constant + 2.5 * LOG (exposure time /
intensity) - magnitude extinction per air mass * air mass + constant *
star color + constant * air mass * star color
The procedure I've adopted is to use a large number of Landolt
standard stars (with accurate B, V, Rc and Ic magnitudes), observed at
a wide range of air mass under clear sky conditions, and perform a
least-squares solution for the various constants. Then, with these
constants, it is possible to convert any unknown star's measured
intensity to magnitude. For star color, such as B-V, an iterative
procedure is employed, and this is straight-forward when using a
spreadsheet.
When the Landolt stars are subjected to the same procedure as
proposed for sue with unknown stars it is possible to assess the
accuracy of the equations with their solved-for constants. I shall now
present scatter plot graphs of the Landolt stars equation magnitudes
versus true magnitudes.
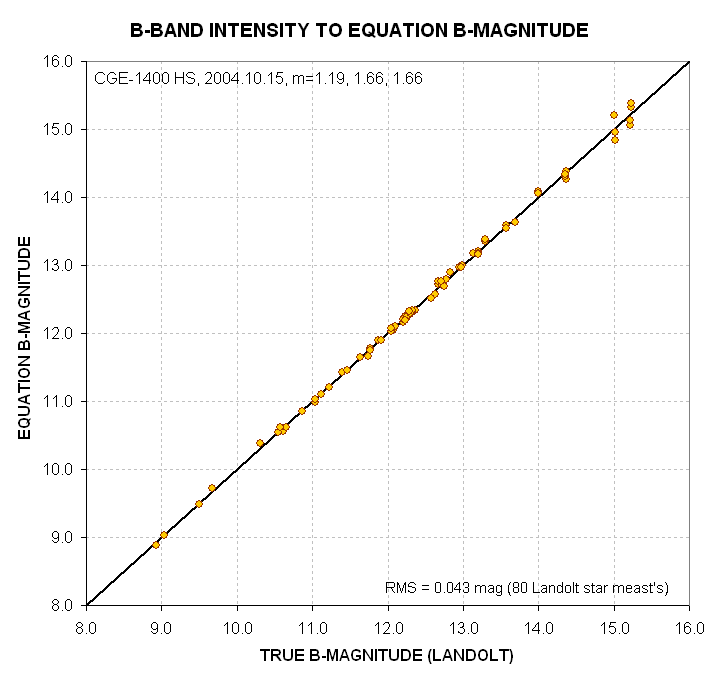
Figure 6. Equation versus true B-magnitude for 56
Landolt stars observed under 4 air mass conditions on 2004.10.15. As
noted in the graph the residuals from a perfect fit have an RMS of
0.043 magnitude (for stars brighter than 14.7)
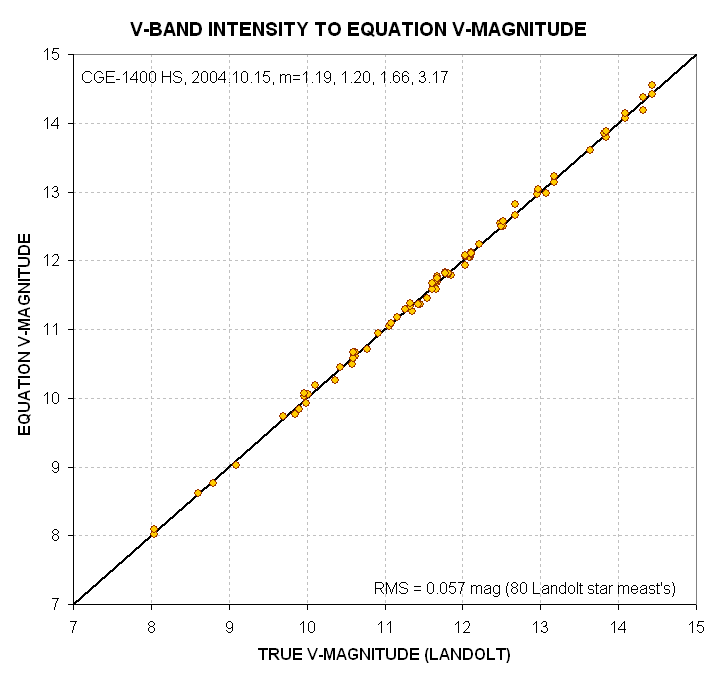
Figure 7. Equation
versus true V-magnitude for 56 Landolt stars observed under 4 air mass
conditions on 2004.10.15. As noted in the graph the residuals from a
perfect fit have an RMS of 0.057 magnitude.
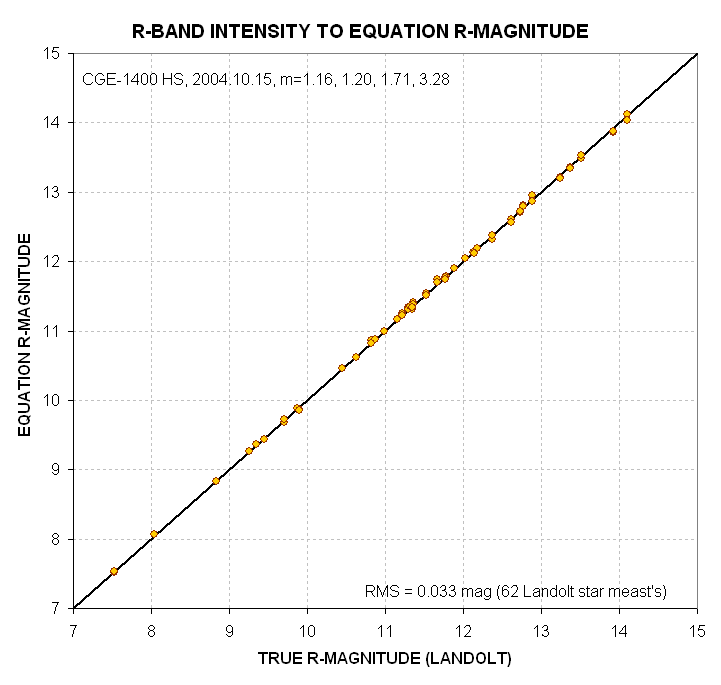
Figure 8. Equation
versus true R-magnitude for 62 Landolt stars observed under 4 air mass
conditions on 2004.10.15. As noted in the graph the residuals from a
perfect fit have an RMS of 0.033 magnitude.
The above graphs use the following equations:
B-mag = 19.31 + LOG (G / Iblu) - 0.228 * m + 0.10
*
((B-V)-0.70) + 0.06 * m * ((B-V-0.70)
R-mag = 19.83 + LOG (G / Ired) - 0.100 * m -
0.110
* ((B-V)-0.70) + 0.02 * m * ((B-V-0.70)
I-mag = 18.723 + LOG (G / Iinf) - 0.09 * m - 0.066 * ((B-V)-0.64) + 0.02 * m * ((B-V-0.64)
where G is exposure time [seconds] (G
stands for "gate time")
Iblu = intensity using B-band filter (ADU counts), Ivis = V-band
intensity, and Ired =
R-band intensity, and Iinf = I-band intensity
m
= air mass, and
B-V is
star color (derived iteratively for unknown stars).
Light Curve for 2004.10.23
On October 23 UT I observed IL Aqr for about 6 hours and found no deviation from constant brightness. Here's my V-magnitude light curve.
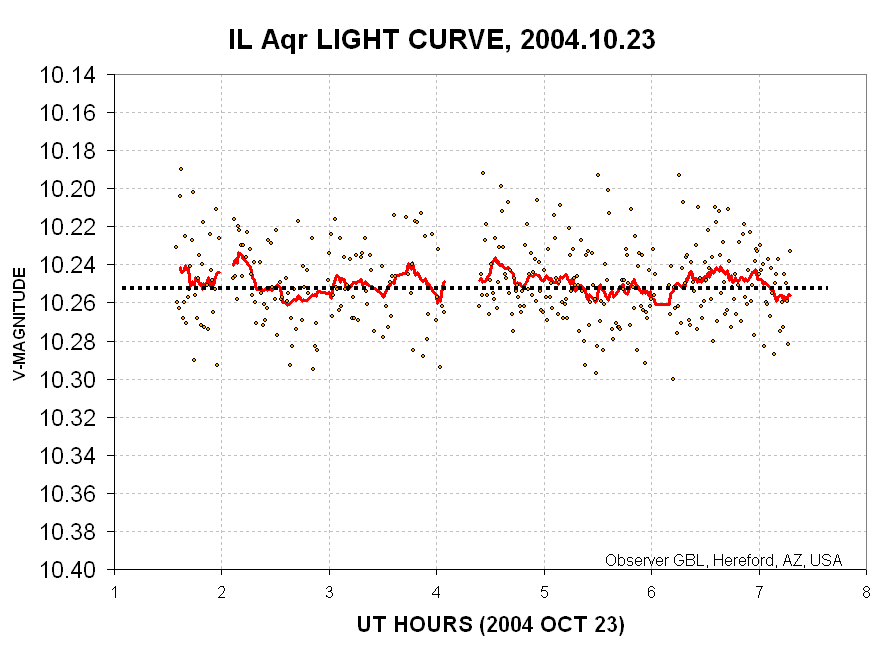
Figure 9. V-magnitude light curve from a 6-hour observing run on October 23 UT. The gap at 4.1 hours is due to having to perform a "meridian flip" (MF) and re-calibrate the autoguider. (No adjustment was made to the post-MF data to bring it into agreement with the pre-MF data.) Each datum is a 30-second exposure, and their RMS departures from the average line is 0.021 magnitude (corresponding to a 20-minute average SE of 0.0041 magnitude, allowing for download overhead). Three reference stars were used, having V-magnitudes of 11.02, 11.48 and 10.42.
The pre-transit data are noisier than the post-transit data due to differences in autoguider performance. The lack of nearby bright reference stars means that some of the IL Aqr measurement uncertainty is due to the stochastics of using a limited number of relatively faint reference stars. Another source of scatter for these obserations was a high level of sky brrightness caused by the moon, which was 10 degrees away.
Miscellaneous Links
XO-1 observations (serves as an exoplanet observing tutorial) http://brucegary.net/XO1/x.htm
Exoplanet observing tutorial at http://brucegary.net/tutorial_exoplanet/x.htm
AAVSO home web page is at http://www.aavso.org/
TransitSearch home web page is at http://www.transitsearch.org/links.htm
TransitSearch tranist ephemeris for all exoplanets candidates is at http://www.ucolick.org/%7Elaugh
TransitSearch Results for TrES-1 is at http://www.ucolick.org/%7Elaugh/TrES-1b.results.html
AAVSO CCD observer's manual is at http://www.aavso.org/observing/programs/ccd/manual/
My TrES-1 observations of three transits is at http://brucegary.net/TrES-1/x.htm
My HD209458 observations of one transit (in 2002) is at http://reductionism.net.seanic.net/HD209458/ExoPlanet.html
My general interest AstroPhotos web page with many links is at http://reductionism.net.seanic.net/brucelgary/AstroPhotos/x.htm
All-sky procedure using equations for converting intensity to magnitude http://brucegary.net/AllSky/x.htm
My observatory in Hereford, AZ is shown at http://reductionism.net.seanic.net/brucelgary/AstroPhotos/m_hardware.htm
and you can reach me at the following e-mail address: b l g a r y @ u m i c h . e d u
____________________________________________________________________
This site opened: October 11,
2004. Last Update: August 16, 2006