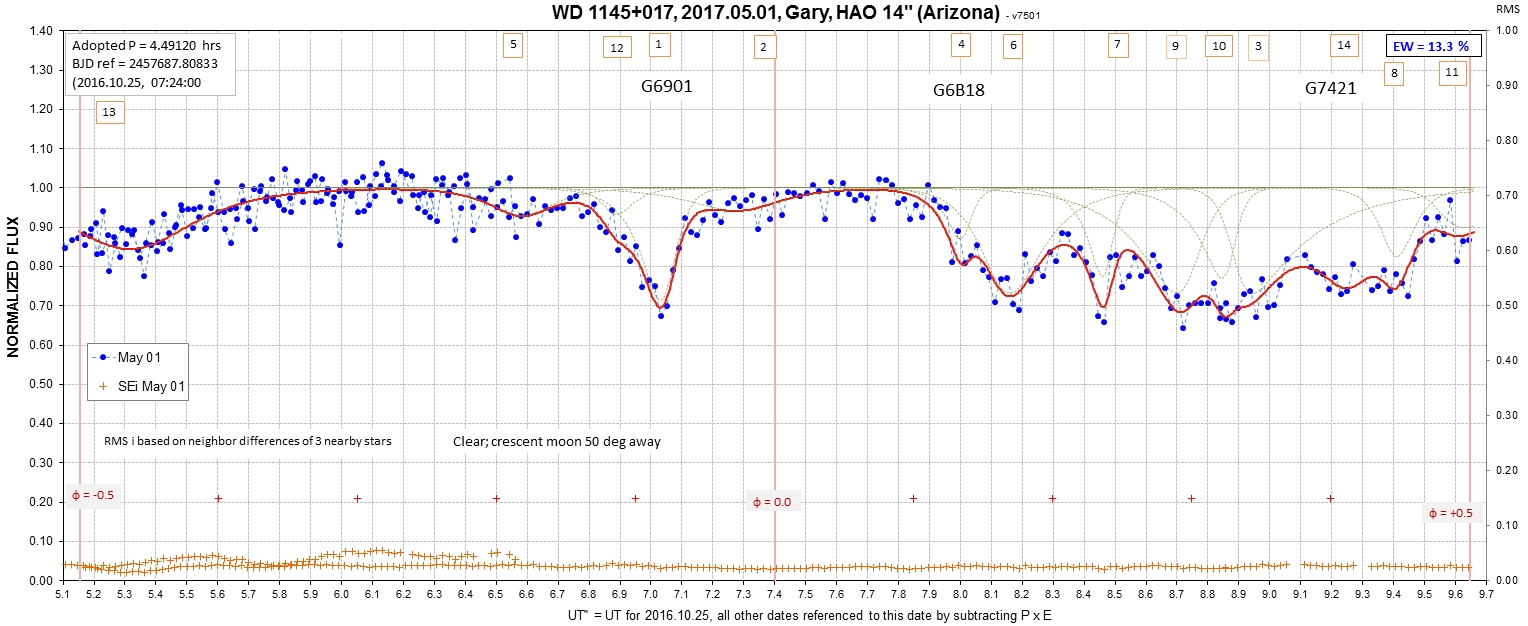
Figure 4. A night's LC from an active year for WD1145. OOT is present ~ 1/3 of the time.
White Dwarf Story
B. Gary, 2024.05.23
This web page
is structured to motivate celestial mechanic modelers to
explain observations of white dwarfs with transiting dust
clouds. It assumes only a modest familiarity with the WD
observations that need to be explained. It is assumed that
dust clouds are produced from collisions and that interloper
planetesimals in highly eccentric orbits are involved. An
ever-present "Roche debris disk" is assumed to exist, created
and maintained by millions of years worth of planetesimal
tidal disruptions at periastron passage. No attention is given
to alternative mechanisms for dust production, and I also
neglect the mysterious matter of how a dust cloud can be
maintained for months without spreading out into nothingness
on daily timescales due to Keplerian shear.
Step 1: Natal Kicks
WD With Low
Packing Fraction (J0139)
WD With Higher
Packing Fraction (WD1145)
WD
With Even Higher Packing Fractions (J0328)
Scenario
Leading to Interloper/Debris Disk Interactions
Questions
for Modelers
Deacription of Packing
Fraction
References
Imagine a WD that is orbited by millions of
planetesimals that used to be in far-out orbits (before the
planetary nebula transition) but are now in highly eccentric
ones with millions having their periastron within one A.U.. At
any randomly chosen time one of the planetesimals orbits so
close to the WD that it feels tidally disrupting forces during
periastron passage. Let's refer to it as an "interloper."
Imagine also that previous interlopers have left
debris that is at the tidal disruption distance in orbits that
have been circularized (due to Poynting-Roberston drag and the
Yarkovsky effect). Encounters with this debris shortens the
interloper's orbital period., so encounters become more
frequent.
Every periastron passage is brief, lasting less than a
minute. But the distance covered is long due to its high speed
(440 km/sec). The interloper's Hill sphere size becomes
irrelevant in determining whether debris undergoes an orbit
change; only impacts matter. Most impacts are grazing because
"impact parameter" values are random.
Whenever a periastron passage produces one or more collisions this may initiate a cascade of collisions. Every collision produces a dust cloud. If the debris has a high "packing fraction" then many collisions can occur. If the "packing fraction" is low, then there may be periastron passages when no collision cascades occur. (For my description of "packing fraction" go to link below.)
2. WD With Low
Packing Fraction (J0139)
Consider the light curve for a WD with a low "packing fraction" (J0139). Every 107 days, approximately, there are dozens of dips, with each dip presumably the result of a collision. The series of dips (the individual ones aren't shown in this graph) last about a week. Notice that the 107-day timing is inexact (e.g., #2 is late). This is because some collision cascades take longer to reach a peak than other cascades. Also, notice that sometimes no cascade occurs (e.g., #6). The greatest deviation from a repeating 107-day occurrence is #9. (It's possible that the early set of dips was produced by a second interloper.)



3. WD With
Higher Packing Fraction (WD1145)
WD1145+017 apparently has more fragments per
unit of radial distance from the WD than J0139 (i.e., a greater
"packing fraction")._This is revealed by two observational
facts: 1) during a dip group the fraction of time for OOT is
greater (typically 30 to 40 %), and 2) each periastron passage
(at 124-day intervals for WD1145) has an activity function that
is a substantial fraction of the periastron interval (FWHM = 60
days for WD1145 instead of 6 days for J0139). The following
graph is essentially chosen at random from an active year.
Approximately 1/3 of the time is OOT.

Figure 4. A night's LC from an active year for
WD1145. OOT is present ~ 1/3 of the time.
The next graph shows "dip activity level" versus date for 4
observing seasons. At the bottom is an offset sine wave with a
124-day period. It does a good job of predicting dip activity.
The black trace is the sum of many Gaussian functions, spaced at
~ 124-day intervals, with amplitude adjusted to fit
measurements. Small adjustments to the best overall repeat
interval of 124 days are permitted because collision cascades
are expected to have variable timescales for reaching peak
activity. Differing amplitudes is also allowed because each
collision cascade can produce different peak levels due to the
randomness of how fragment orbits are packed. Each Gaussian
function is also allowed to have a slightly different width. A
typical FWHM width = 60 days.

Figure 5. Dip activity for the
first 4 season's of ground-based measurements. The sinusoidal
trace (tan, at bottom) has a period of 124 days), and it is
correlated with measurements of dip activity. The black trace
that fits data was produced by a repeating pattern of Gaussian
shapes with height and widths adjustments. Small date shifts
were also applied to improve fit.
To see details of the above graph, one observing
season at a time, go to this link.
If the 124-day periodicity of dip activity is real
then it should show up in a periodogram. It does!

Figure 6a. Lomb-Scargle periodogram of the
WD1145 dip activity plot for the first 6 observing seasons of
ground-based data in my archive. The main feature is a period
of 0.346 years, or 126 days. The presence of features with
longer periods are due to the year-and-longer timescale
variations (apparent in Fig. 5).
The next graph
is a periodogram for a version of dip activity in which
each season's level was either increased or decreased in
order to achieve approximate equality of peak activity
level for that season. The purpose in doing this is to
eliminate periodogram features produced by year-and-longer
timescales. This should produce a "cleaner" solution for
the main feature.

Figure 6b. Lomb-Scargle
periodogram of the WD1145 dip activity plot for the first
6 observing seasons of ground-based data in my archive
after normalizing individual seasonal variations to the
same approximate activity level. The main feature is a
period of 0.342 years, or 125 days. The presence of
features with longer periods are reduced, as expected,
which allows for a "cleaner" solution for the main
periodicity.
Indeed, the expected
"cleaning" of the periodogram was achieved, and the main
period stands out more prominently. The interloper period is
now estimated to be 125 days. (The second highest feature has
P = 94 days; if real, iy could be a second interloper.)
The next graph shows WD1145 dip activity level for
11-years, using a log scale for representing activity. The
green trace is an eyeball fit using a Poisson function.

Figure 7. Activity for the
last 11 years, using a log scale for activity. The thick green
trace is a Poisson function (lamda = 2), added to an
ever-present 0.25 % activity level.
The above graph's green trace calls to mind a scenario in which
a big collision occurred in 2015, and that it initiated a
sequence of secondary collisions. Yes, but the modulation of the
green trace, i.e., the black trace, inspires a more nuanced
model: a big collision happened in 2015 by the periastron
passage of an interloper, and every subsequent periastron
passage instigated a collision cascade (of duration ~ 60 days,
FWHM) whose dip activity level exhibited a Poisson amplitude
(green trace) versus date, whose shape was influenced by an
exhaustion of fragments in the WD's "Roche debris disk"
periastron vicinity (described below).
During the peak activity years of 2016 and 2017 it was
common to observe a dozen or more dips per 4.5-hour orbit. Since
dips lasted for a couple weeks, typically, it was tempting to
imagine that the number of fragments that were capable of
producing dust clouds numbered 1000 or more. If after a
few years there was an "exhaustion" of fragments that could be
involved in a interloper-initiated collision cascade it may be
possible to model how many fragments (capable of producing dust
clouds) were present prior to the 2015 collision.
Support for a big collision in 2015 comes from a
waterfall plot that shows a set of drift lines in "orbit
phase/date space" that radiate from the date 2015 August. A
reviewer of our article that reported the first comprehensive
set of ground-based LC observations of WD1145 (Rappaport et
al., 2016) was the first to notice this pattern.



We never argued for the reality of a slowly decreasing
A-disk period, but if real it might help with modeling. For the
past 10 years almost all observed dips have a period similar to
the ones in the above figure. We occasionally observe dips with
longer periods. For example, the next graph shows all 6
Kepler-based periodicities (converted to radial distance from
the WD):



4. WD
With an Even Higher Packing Fraction (J0328)
J0328-1219 is a WD with a presumed even higher packing fraction.
Dips are present almost all the time; OOT levels are sometimes
not present. The next figure is a LC illustrating this.

An analysis of this WD's "dip activity level" versus
date has not been performed, so it is not yet known if an
interloper is present. If an interloper is present it is
producing dip groups with long duration (comparable to, or
longer than, the interloper's orbit period).
J0107+2107 is another WD with a high packing fraction. It has so
many closely-spaced dips that OOT time has maybe never been
observed. I won't present a LC for it here, but it's worth
mentioning because it illustrates the concept that WDs with
transiting dust clouds extend to those with extremely dense dip
activity, which means that very high packing fractions are
possible.
5.
Scenario Leading to Interloper/Debris Disk Interactions
This web page's introductory section suggested that a sequence
of events leading to interloper interactions with a preexisting
"Roche debris disk" starts with a "natal kick" to the WD when it
undergoes an anisotropic shedding of (half) its
atmosphere, producing a planetary nebula; this was described by
Akiba, McIntyre and Madigan (2024). WD velocity changes
("kicks") within the range of 1 to 3 km/s were capable of
changing the orbits of distant planetesimals enough so that some
of them befan to orbit retrograde. This means that there must be
a population of planetesimals that had orbits bringing them
close to the WD's Roche radius (distance where tidal disruption
could occur).
We can now speculate what the second step might be.
The first time a planetesimal passes close to the WD's Roche
radius it may shed some of its material. This material will
initially be in the same highly elliptical orbit as the parent
planetesimal. However, after many periastron passages (of both
the parent planetesimal and shed debris) the debris, because it
is smaller and less massive, will be affected by
Pointing-Robertson drag and also the Yarkosky effect. Neither of
these effects will change the orbit of the planetesimal because
it is too massive. But PR drag will reduce the orbital momentum
of debris that is smaller than some size, such as 1 km radius
(?). The Yarkovsky effect will reduce orbital momentum of
fragments rotating in a retrograde direction, and that are
smaller than some size (possibly also 1 km in radius?). After
many periastron passages the debris, smaller than some size,
will "circularize" their orbits to a radius close to the WD's
Roche radius. This may require millions of years.
During that millions of years that small debris
circularizes, there mau also be many additional interloper tidal
passages and shedding events. A steady-state of interloper
sheddings, and simultaneous circularizations, must exist.
The third step is about an interloper passing through the disk of smaller-sized debris at the WD Roche radius. That's what i've been referring to as the "Roche debris disk." Each planetesimal periastron passage is an opportunity for impacts. When the larger planetesimal impacts a smaller fragment, the smaller fragment will be smashed into to a set of smaller fragments with a "particle size distribution," or PSD, that may extend down to sub-micron radii. The smallest particles can be thought of as a dust cloud which can both scatter and absorb the WD's light (producing dips), whereas the larger ones, with radii of meters and tens of meters, can be viewed as an addition to the Roche debris disk. The large debris will be in orbits whose parameters are changed by random amounts from the parent's orbit. The new debris may be in orbits that cause them to impact other debris. If so, then a cascade of collisions could begin. Whether or not a collision cascade is initiated by the initial collision (the planetesimal and one debris fragment) depends on the debris disk's "packing fraction." For a high packing fraction it is more likely for a collision cascade to occur.
The circularized fragments that constitute the "Roche debris disk" may be considered the product of a steady-state production process (with timescales of millions of years) and a steady-state destruction of these fragments due to impacts with more recent interlopers. The rates of production and destruction will be one factor determining "packing fraction."
Here's a diagram of the periastron path of an
interloper in an elliptical orbit traversing the WD1145 "Roche
debris disk." The 6 Kepler disk systems may simply be the inner
part of WD's "Roche debris disk."

Figure 16. A possible path of a WD1145
interloper, which assumes it passes through the long-lived
"Roche debris disk" at the WD's Roche radius. I assume that
the 6 Kepler periodicities correspond to the inner part of the
"Roche debris disk" and that the disk will last for much of
the WD's lifetime. (A more realistic diagram would include
several interlopers in elliptical orbits, with farther-out
periastron distances and random longitude orientations.)
Over time each interloper will migrate inward, both
slowly and abruptly, due to encounters with material in it out
orbit portions, and it will "take its turn" being tidally
disrupted and replenishing the "Roche debris disk." In fact,
there may be times when more than one interloper is passing
through the "Roche debris disk" (at different periastron passage
intervals). At any given time there will
be gaps in the Roche disk due to passes by previous interlopers.
The slow inward migration of the
interloper's periastron distance will produce collision cascades
that only progress inward. This speculation is supported by
WD1145 observations. Since debris in this disk may have taken
millions of years to circularize after being tidally separated
from an interloper, the "Roche debris disk" may consist of
fragments from many tidally disrupted interlopers.
The previous section has many loose end questions that will be a challenge to modelers. For example:
1) How often will the "natal kick" produce
planetesimals that come close to the WD's Roche radius?
2) How long will these planetesimals (which I rename
"interlopers") stay close to the Roche radius?
3) What sizes of debris will be affected by PR drag and the and
Yarkovsky effect?
4) How long will it take for PR and Yarkovsky to circularize
debris?
5) How much debris will be shed by an interloper during each
periastron passage, and how does that limit the "lifetime" of
the interloper?
6) How big a radius span will the "Roche debris disk" have?
7) Will gaps form in the debris disk, leading to a set of
narrower debris disks (resembling WD1145's set of 6 lesser
disks)?
8) What will be the PSD from the debris after a
interloper/debris collision?
9) How often can we expect the initial collision
(interloper/debris) to produce secondary collisions (i.e., a
collision cascade)?
10) Is it reasonable for debris/debris collisions to form dust
clouds that match observed dips?
11) Can packing fraction, or the PSD function,
be inferred from the duration of dips associated with a
single periastron passage (e.g., 6
days vs. 60 days)?
12) Can packing fraction, or the PSD function,
be inferred from the variability of timing for peak dip
activity?
Then there is another set of questions (not suitable for celestial mechanics analysis) that have puzzled modelers for the last decade, such as:
1) What is the mechanism for dust production
(collisions, or sublimation and recondensation after thermal
escape)?
2) What is the dust destruction mechanism (sublimation,
Keplerian shear, PR, Yarkovsky)?
3) Why is there an absence of small dust (radii < 1 micron
for WD1145, radii < 0.1 micron for J0328)?
Tom Kaye and I are observationalists. We want to create puzzles
for modelers. I think we and other observers of "transiting WD
dust clouds" have created a big enough puzzle for modelers to
"take on" the task of answering some of the above questions.
6.
Description of Packing Fraction
Imagine a 2-D disk with circular radii from a1 to a2.
Within this 2-D space it is possible to have orbits described by
semi-major axis distance, eccentricity and orientation of
periastron (line of apsides). Each orbit has a location in 3-D
parameter space. If we assign a mass to the orbiting object then
we have also specified a Hill sphere radius. No other object is
allowed within this 4-D parameter volume. (Actually, there's one
more parameter which we haven't specified: the object;s location
in the specified orbit; but let's keep things simple and neglect
that parameter).
When a second object is created it can't be placed in
the same 4-D volume without risking eventual collision with the
first object. By placing the second object in a different
(non-conflicting) orbit we've used up another increment of 4-D
space that was initially available.
I think the rest of this argument is obvious. There is
a maximum number of orbits that can exist without collisions
(assuming each object has a specified mass). The "packing
fraction" can be said to be 1.0, or "full." when the maximum
number of objects are present. Clearly, if we start with a
packing factor of 1.0, any change in orbit of an object will
lead to at least one collision. And that collision could lead to
a third collision, etc..
It is also obvious that with only two objects located at random locations in the disk, when one object's orbit is changed it is unlikely to collide with the other object. So, the probability of initiating a collision cascade is related to packing factor.
For intermediate packing factor values the temporal
length of the cascade will depend on the number of collisions
that eventually occur. In addition, the time of maximum
collision occurrence will be related to the total number of
collisions and how long the sequence lasts.