PHOTOMETRY FOR DUMMIES: METHOD #9
Bruce L. Gary, Hereford Arizona Observatory (G95)
Last updated 2011.06.04
~ 0.05 mag SE, Convert Carlsberg
r' and 2MASS JK to B,V,Rc,Ic,i',z' (10 Minutes)
This method will only work for stars between -30 and +50
degrees declination. There are two situations for which this procedure
can be used: 1) you don't have an image of the target star field, and
2) you do have an image (or image set) of the target star field. Slightly
better results can be obtained using an actual image of the target star
and nearby stars, but it entails more work and may not be worth the
extra effort for most users. It also involves use of a free program, DS9.exe.
(If you don't have DS9.exe installed on your computer, go to the bottom
of this page for instructions on doing it; it's a free program.) This
procedure is meant for "main sequence" stars (~90%) and star fields that
are not highly reddened by interstellar dust. However, for Rc, Ic, i' and
z' there shouldn't be a problem for even non-main sequence stars or reddened
star fields.
Procedure When You Don't Have An Image of
Target Star Field
Browse to the VizieR web site: http://vizier.u-strasbg.fr/viz-bin/VizieR
Here's what the (new portal) VizieR web page looks like (after user
enters desired catalogs and target star coordinates):
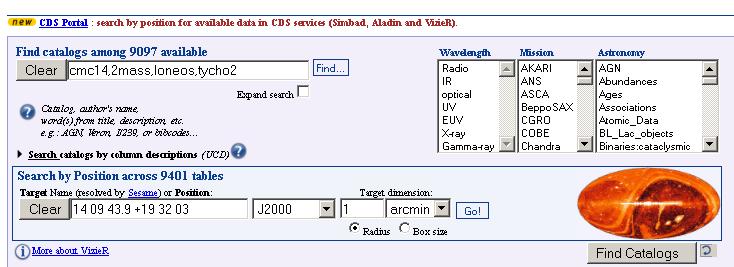
Figure 1. VizieR input page, where user enters desired
catalogs and star coordinates.
User first enters "CMC14, 2MASS, LONEOS, Tycho-2" (case doesn't
matter) and RA/DE coord's, then clicks Go. This will produce an output
that looks like this:
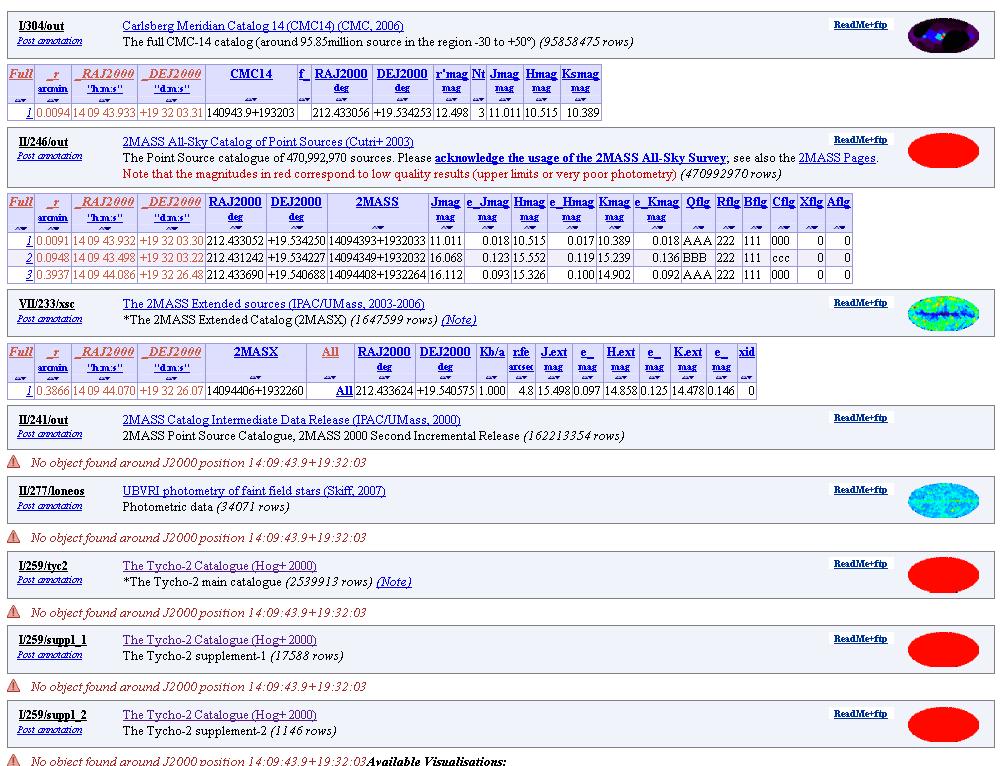
Figure 2. VizieR result page, showing star mag's at the
requested RA/DE coordinates. Nothing was found for LONEOS and Tycho-2.
In the CMC14 section the first entry is closest to the target coord's,
so this is the row from which we note that r' = 12.498.
In the 2MASS section the first entry is closest to the target coord's,
so this is the row from which we note that J = 11.011 ± 0.018
and K = 10.389 ± 0.018.
The LONEOS section can be ignored for now. It's used to assess whether
this star is suitable for use with the rJK conversion algorithm (because
of the star's spectral energy distribution, SED, departing from normal for
main sequence stars). This is treated in a later section of this web page.
Download a small spreadsheet for converting magnitudes from this link:
Converting-rJK-to-BVRcIci'z'.zip
Unzip and run it. Enter mag's and SE's in the input section light
blue cells; it will then look like this:
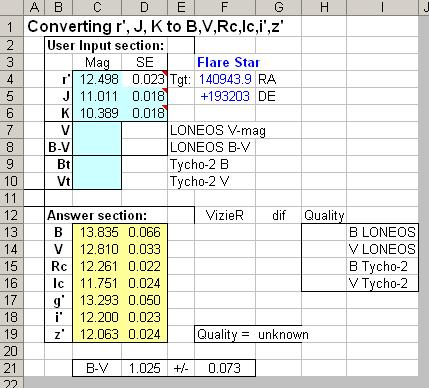
Figure 3. Spreadsheet input (light blue cells) and
output results for B, V, Rc, Ic, g', i' and z' (yellow cells).
Note the answers in the yellow cells for B, V, Rc, Ic, g',
i' and z'.
Don't enter an SE for r' because it's calculated automatically by
the spreadsheet using the SE(r') relation reported by the CMC14 project:
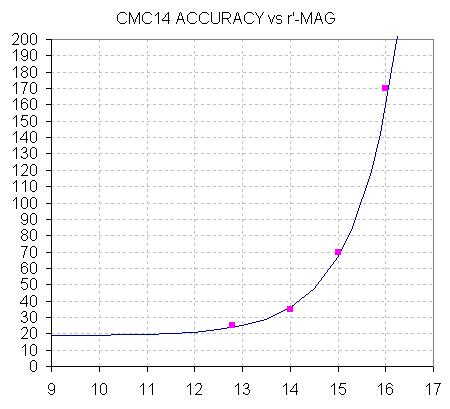
Figure 4. r' accuracy SE [mmag] versus r' (according
to a CMC14 project report).
The spreadsheet calculates most-likely mag's for B, V etc using results
of a multiple-regression analysis that I performed using stars calibrated
in BVRcIc bands by Landolt (2009) and calibrated in u'g'r'i'z' bands at
the USNO by Smith et al (2002). Of the 158 stars in the Smith et
al catalog only 94 stars are in common with the Landolt (2009) catalog.
My analysis uses 93 of these stars (my bookkeeping lost track of one of them);
these are the best fully-calibrated stars in the sky, having Landolt (2009)
magnitudes for BVRcIc and Smith et al (2002) magnitudes for u'g'r'i'z'.
The J-K colors are within the range -0.2 to +1.2. Each filter band was subjected
to an objective and iterative outlier rejection procedure. An outlier for
this analysis is defined as a value that departs from a model fit by more
than 2.7 × RMSi, where RMSi is the population RMS (including the candidate
outlier) for that iteration. When the total number of values ~ 93 this outlier
criterion will typically reject a valid datum once per 10 uses. This assumes
the set of values consist of two populations: a Gaussian and outliers.
The entire list of 94 stars can be found in a spreadsheet at: 1335 & 94 star list.zip. This
spreadsheet also includes a listing of 1335 stars that have been calibrated
by Landolt (1992), Landolt (2009) and Smith et al (2002).
If you don't want to use this spreadsheet you may use the equations
and constants shown in the following figures:
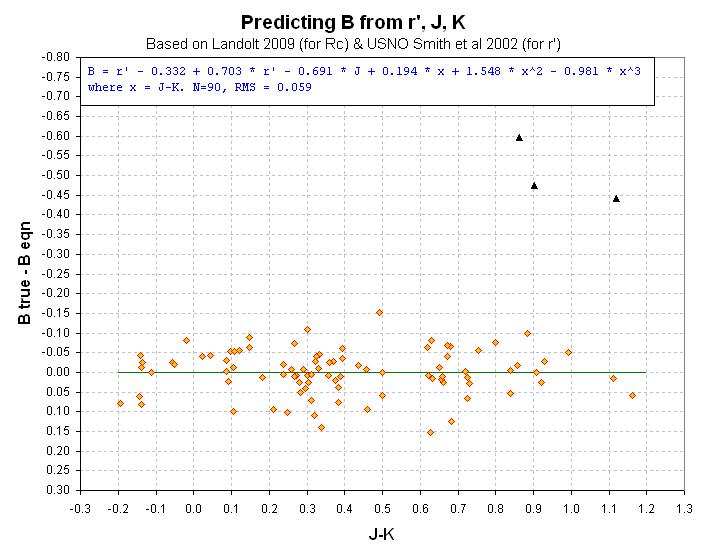
Figure 5. Scatter plot of true B magnitude minus equation
B magnitude versus J-K star color. Note that 3 B-mag's were "outliers" (3%,
due to actual star perculiarities, not measurement errors), being
brighter than the rJK equation predicts.
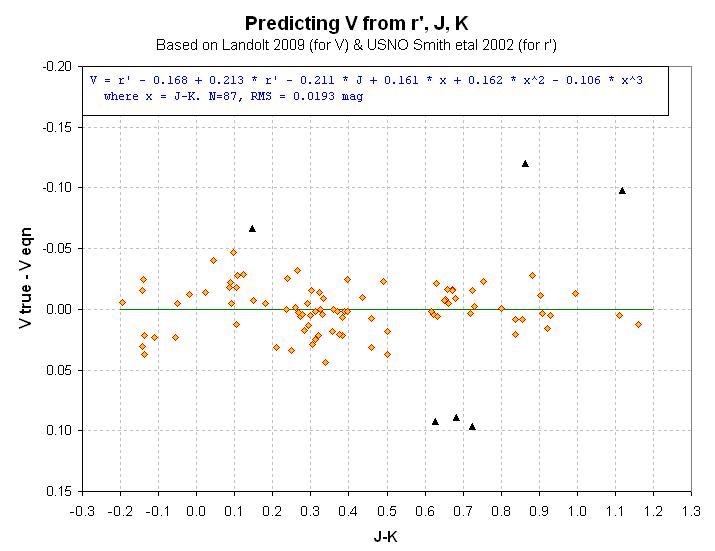
Figure 6. Note that 6 V-mag's were "outliers."
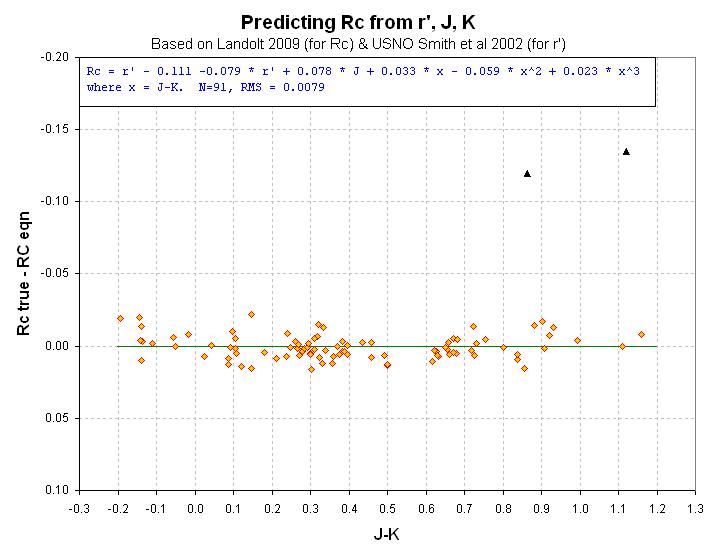
Figure 7. Note that only 2Rc-mag's were "outliers."
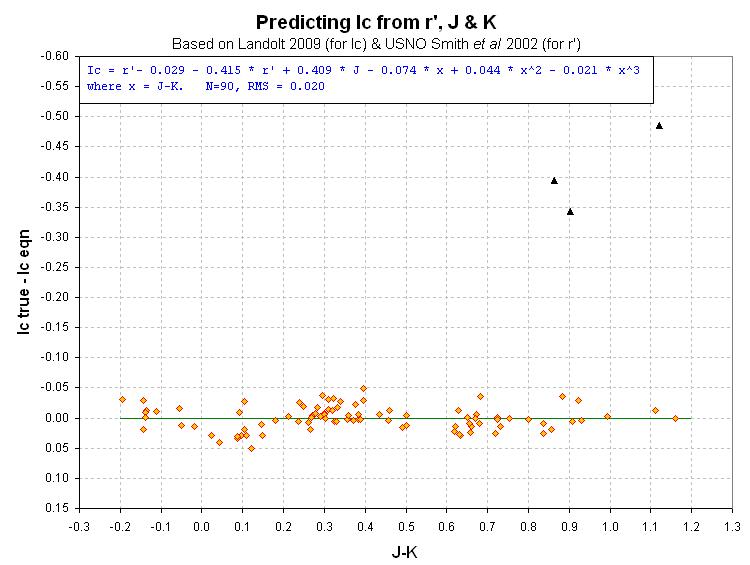
Figure 8. Note that 3 Ic-mag's were "outliers."
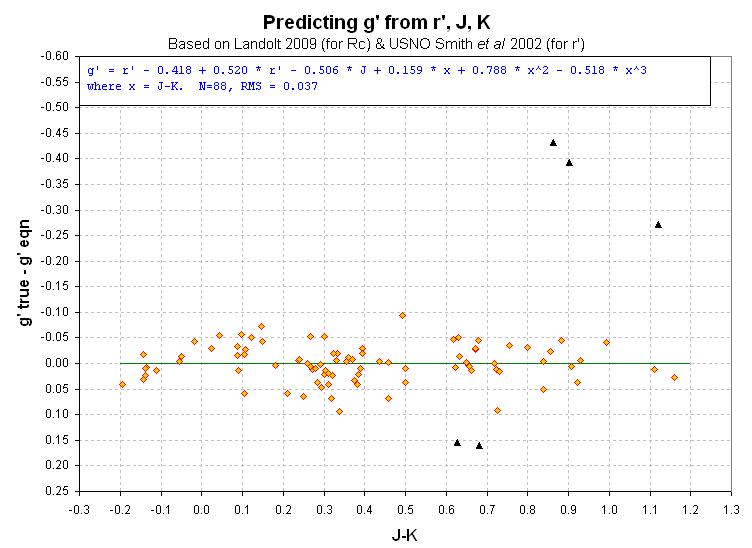
Figure 9. Note that 5% of g'-mag's were "outliers" (due to actual
star perculiarities, not measurement errors).
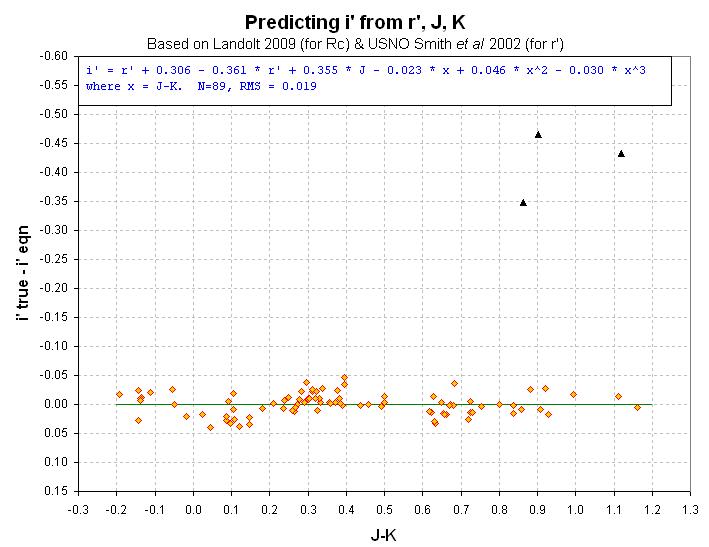
Figure 10. Note that 3 i'-mag's were "outliers."
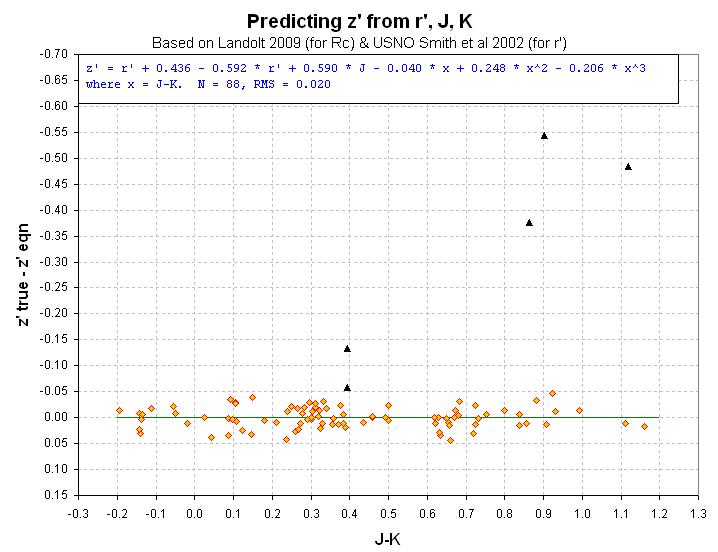
Figure 11. Note that 5 z'-mag's were "outliers."
These figures show error scatter for ~ 90 well-calibrated
stars after calculating B, V, Rc, Ic, i' and z' (using the equations
shown) when good quality r'-band mag's were used (SE < ~0.004, ?).
The measured RMS values are 0.059, 0.019, 0.008 and 0.020 mag for B, V,
Rc and Ic. These RMS values are the orthogonal sum of errors propogated by
r'_SE, J_SE, K_SE and star spectral energy distribution differences (including
a small amount of interstellar reddening). I calculate that the last
component (star SED differences and reddening) = 0.050, 0.017, 0.007 and
0.019 mag for B, V, Rc and Ic. For a specific target star situation,
where we are using a single Carlsberg r' magnitude and J & K magnitudes
with specific SE values, we can orthogonally add a Carlsberg r' SE (typically
~ 0.025 ) to the other two sources of SE to arrive at a final SE. This
is done in the above spreadsheet. Typical final SE values are 0.068,
0.035, 0.025 and 0.025 mag for for B, V, Rc and Ic. In the next table
note how these SE values compare when using the JK-only procedure
(as reported by Warner and Harris, 2007), the rJK with CMC14 r' procedure
and the rJK with USNO Smith et al 2002 r' procedure.
Table 1 - Typical Final SE's When Using CMC14
r'
JK-only rJK
rJK
CMC14
r' USNO r'
B 0.080 0.067
0.059
V 0.050
0.033 0.019
Rc 0.040
0.022 0.008
Ic 0.035
0.025 0.020
All bands exhibit significantly improved SEs using the rJK equations
compared with the JK-only equations.
More About "Outlier" Stars
The so-called "outlier" stars must have "spectral energy density" (SED)
functions that differ from the average. The approximate outlier percentages
(for the group of 93 fully-calibrated stars) are given in the following
table.
Table 2 - Typical "Outlier" Incidence
B 3%
V 6%
Rc 2%
Ic 3%
g' 5%
i' 3%
z' 5%
One star was an ooutlier in every one of the previous 7 figures, and another
was an outlier in 6 of the 7 figures. This should serve as a warning about
using the rJK conversion equations and expecting the SE accuracies cited
above to be correct. To investigate the outlier matter further, consider again
the B-band scatter plot (repeated below).

Figure 5 Repeat. Scatter plot of true B magnitude minus equation
B magnitude versus J-K star color.
The outlier star with J-K = 0.90 will be used as an example of a "bad
star." The star with J-K = 0.91, that agrees with the model, will be used
as an example of a "good star" in what follows.
The stated SEs will only be valid if something is explicitly done to guard
against the star-of-interest being an outlier star. One precaution is to
compare the rJK-derived B-mag with the Tycho-2 based B-band magnitude, and
if they differ by more than 0.25 magnitude, for example, the star-of-interest
will probably be an outlier. If the star is an outlier on this basis then
it should be viewed as a probable outlier for all other bands.
Here's an illustration of how to identify the "bad star" in the above
figure (at J-K = 0.90) as an outlier. The rJK-converted B-mag for this star
is 13.483, while the Tycho-2 catalog has Bt = 13.663 and Vt = 11.376.
Using the conversion equation Tycho-2 based B = Vt + 0.760 * (Bt - Vt),
we derive Tycho-2 based B = 13.114. Therefore, B(Tycho-2) - B(rJK) = -0.369,
and this confirms the star to be an outlier. These calculations can be performed
easily with the rJK spreadsheet, starting with the VizieR input and then
the rJK spreadsheet:
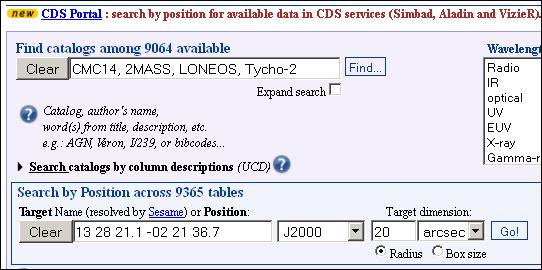
Figure 12. VizieR input fgor the "bad star" showing the catalog
selection that I recommend for any use of the rJK spreadsheet.

Figure 13. rJK spreadsheet for "bad star" showing a discrepancy
of -0.369 mag comparing Tycho-2 based B-mag with the rJK-based B-mag (cell
G15).
In this figure both the B- and V-mag values based on Tycho-2 differ from
the rJK-based values by large amounts. The "Quality" score (simply a probability
function using an assumed FWHM based on the RMS from Fig's 5 and 6) is close
to zero, suggesting that the rJK magnitudes not be used because this star
is a "SED ooutlier."
The Tycho-2 catalog is limited to V ~ 11, approximately, so for fainter
stars another catalog has to be relied upon for determining if the star
is a SED outlier. I've tentatively chosen to use the LONEOS (2003) catalog
for this purpose.
To show that the rJK spreadsheet identifies good stars a good, here's the
rJK result for the "good star" identified in Fig. 5 at J-K = 0.91.
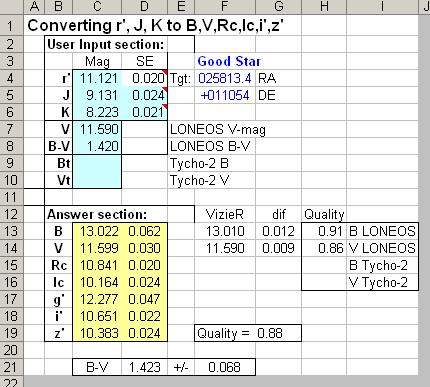
Figure 14. rJK spreadsheet for "good star" showing only small
discrepancies between LONEOS-based B- & V-mags and the rJK-based B- &
V-mags (cells G13:G14).
For this star there are no Tycho-2 magnitudes, because it is fainter than
the 11th V-mag limit, but LONEOS does have entries for V and B-V. The
Quality score for this star is close to one, so it is not a SED outlier.
Scoring the rJK Algorithm Using Landolt Stars Not Used in Determining
rJK Coefficients
The USNO by Smith et al (2002) catalog contains
u'g'r'i'z' magnitudes for 158 stars, 94 of which are found in the Landolt
(2009) catalog of BVRcIc magnitudes for 598 stars. Let's calculate BVRcIc
using the rJK algorithm for some of the 1207 Landolt (2009) stars that weren't
included in the USNO SDSS catalog, and therefore weren't included in deriving
rJK coefficients. For r' we'll use the CMC14 catalog, as before. This will
be a labor-intensive evaluation, so the following table will be updated as
my time permits.
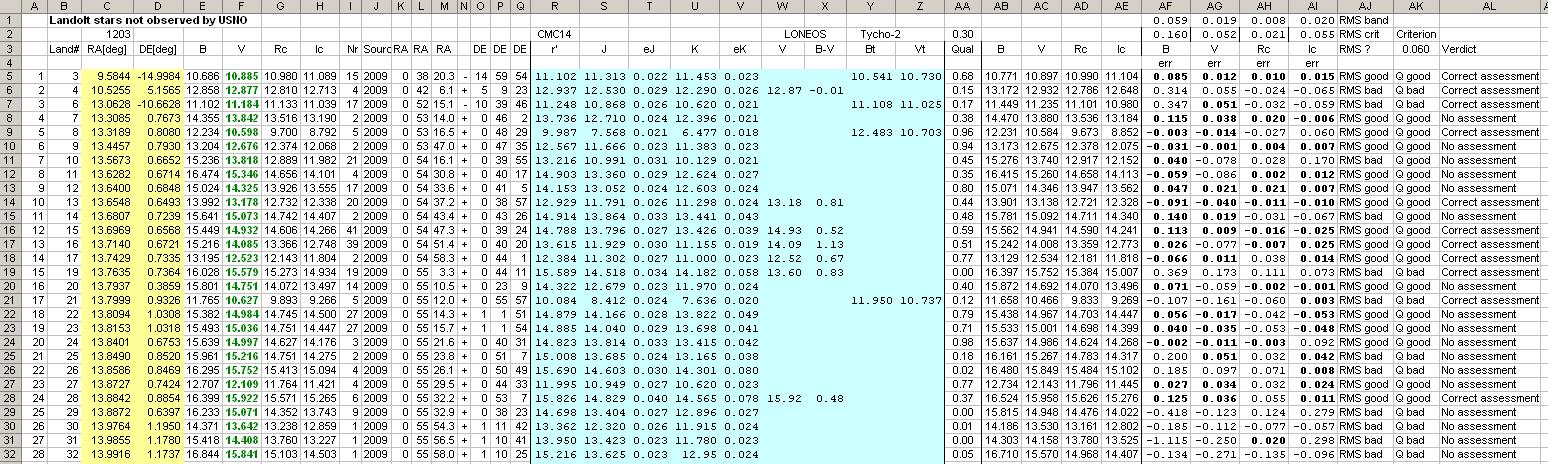
Figure 15. Assessment of rJK algorithm using Landolt stars not
used for determining conversion coefficients. Magnitude errors columns AF:AL
are bold when the magnitude error is less than 2.7 x RMS for the band in
question.
An assessment for "SED Outlier" status can be made for only about 1/3 of
stars (11 out of 28, so far) because the Tycho-2 and LONEOS cataloges aren't
comprehensive enough. When an assessment can be made it is usually correct
(11 out of 11, so far).
Finally, here's a result for a faint "flare star."
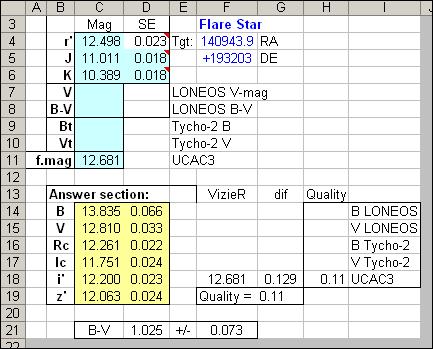
Figure 15. rJK spreadsheet for a star that's too faint to be
included in either the Tycho-2 or LONEOS catalogs but is present in the UCAC3
catalog.
This illustrates the reality for faint stars; they can't be identified
as "SED normal" or "SED outliers" based on B-magnitude differences. At least
in this case we can assess the target star's suitability for rJK use based
on the V-magnitude difference with the UCAC3 catalog's f.mag (an attempt
to approximate V-mag). The differenceof 0.129 mag is large compared with
the 0.019 mag RMS in Fig. 6, so we should assume that this star could be
a SED outlier. If the star really is 0.129 mag brighter in V than the rJK
algorithm solution, and if you're desperate for estimating the other magnitudes,
try assuming that the departure from rJK increases monotonically in going
to shorter wavelength bands starting at r'. I think it should be safe
to adopt the rJK solutions for Rc, Ic, r', i' and z' since they're all within
the region covered by r' toK.
If the star were fainter than those in the UCAC3 catalog then all we could
say is that the rJK results just have to be viewed as having a ~94% probability
of being acceptable, which assumes that the star wasn't identified for evaluation
for a reason that could be related to a SED anomaly (e.g., "flare star").
That's when a single image with any of the short wavelength filtes can "come
to the rescue." This is treated in the next section.
Procedure When You Do Have An Image of Target
Star Field
If you use an image of the target star field it's possible
to improve the accuracy of the target star's V, Rc, Ic, i' and z'
magnitudes (there's a small improvement for B). These improvements are
due to the fact that many nearby stars with CMC14 r'-mag's can be used
to establish a set of telescope photometry constants associated with
the image. Instead of r' SE being ~ 0.025 mag it is possible to achieve
a smaller value for the ensemble of CMC14 stars. Consider the example of
using 25 nearby stars with CMC14 r' mag's. The SE on r' for the target
star would decrease from 0.025 to ~ 0.005 mag if the system of Carlsberg
stars had zero systematic error. This won't be the case, of course, since
individual CMC14 stars are uncertain by an amount that's the orthogonal
sum of the star field's systematic error and the individual star's measurement
by the CMC14 reduction pipeline. Using many CMC14 stars in an image reduces
only the individual star SEs, and as the number of stars increaes the underlying
systematic error for this star field becomes the dominant component of SE
for the average of all stars. If many CMC14 stars in an image are used then
maybe the SE for the target star might decrease to an asymptotic value as
low as ~ 0.010 mag, for example. The corresponding SEs for B, V, Rc, Ic,
i' and z' would then be ~ 0.057, 0.022, 0.012, 0.022, 0.020 and 0.024 mag
(assuming typical SEs for J and K).
There's a caveat that should be repeated here. If the target
is an "outlier" (not a main sequence star, or if the star field is
in a region of the sky with high interstellar reddening) then the conversion
equations (from r'JK to BVRcIc) will yield target star magnitudes that
are systematically offset from true. This effect will be smallest for
Rc, a little larger for Ic and i', larger for V and largest for B.
Here's a brief description f the CMC14. It contains ~ 94 million
stars, and in a typical image (FOV 13 x 19 'arc) there are 2 to 4 dozen
stars with r' < 14. The r' accuracy varies with r' as shown in Fig.
4, above. It is safe to use r' < ~14.5. For fainter stars it is advisable
to use an image with the target star in the FOV, as described in this section.

All-Sky Alternative
For more accurate mag's at all bands consider performing an all-sky
observing session, as described at http://brucegary.net/allsky2011/
____________________________________________________________________________________________
Disregard the following.
R-mag = (20.0 +/- 0.1) - 2.5 * LOG10
( FLUXr / g ) - (0.13 +/- 0.01 ) * m
where FLUXr = "intensity" of the asteroid using the R-band
filter, g = exposure time, m = air mass. The constant 0.13 +/- 0.01
is my site's extinction {magnitudes per air mass). The constant 20.0
+/- 0.1 is unique to my telescope system and is the number that must
be calibrated once per year (or whenever the configuration changes). Each
filter has a different pair of constants, and I'm just illustrating the
equation for converting intensity to magnitude for one filter.
Procedure for Downloading Free Program DS9.exe
The
References
Smith, J. Allyn, et al, 2009, AJ, 123, 2121-2144.
Landolt, Arlo U., 2009, AJ, 137, 4186-4269.
Return to Photometry for Dummies
____________________________________________________________________
This site opened: January 1, 2005. Last Update: 2011.06.13a
















