TRANSMISSION GRATING SA-100 AND CERES SPECTRUM
B. Gary, Last modified 2015.07.31
This web page describes how I have used the SA-100 transmission grating to create a spectrum of Ceres for ~ half of a rotation. I conclude that I don't know how to obtain and process SA-100 images for achieving spectra that are as accurate as can be obtained using the FC filters. This conclusion is based on the finding that the variation of geometric albedo with rotation is slightly greater for the SA-100 data than the FC data.
Observations

After several short observing sessions devoted to learning how to observe with the SA-100, and reduce the images, I observed Ceres on two nights: Jun 05 (cut short by clouds) and Jun 06 (lasting 4.5 hrs, from twilight to Ceres setting below20 degrees). A sun-like secondary standard star (59 Vir) was observed at intervals of ~1 hr for ~ 15 min. Exposure times were 4 seconds for 59 Vir and 10 seconds for Ceres, which assured that the spectrum would not be saturated. On May 31 Gamma UMa was observed for the purpose of establishing pixel to wavelength conversion equation.

Reduction Process

Standard calibrations were used for all images (bias, dark and flat). Groups of images for a target (GUMa, 59 Vir or Ceres) were aligned, checked for quality (sharpness & lack of cloud effects) and median combined. The combined images was then measured using a horizontal box photometry tool in MaxIm DL (Fig. 1).


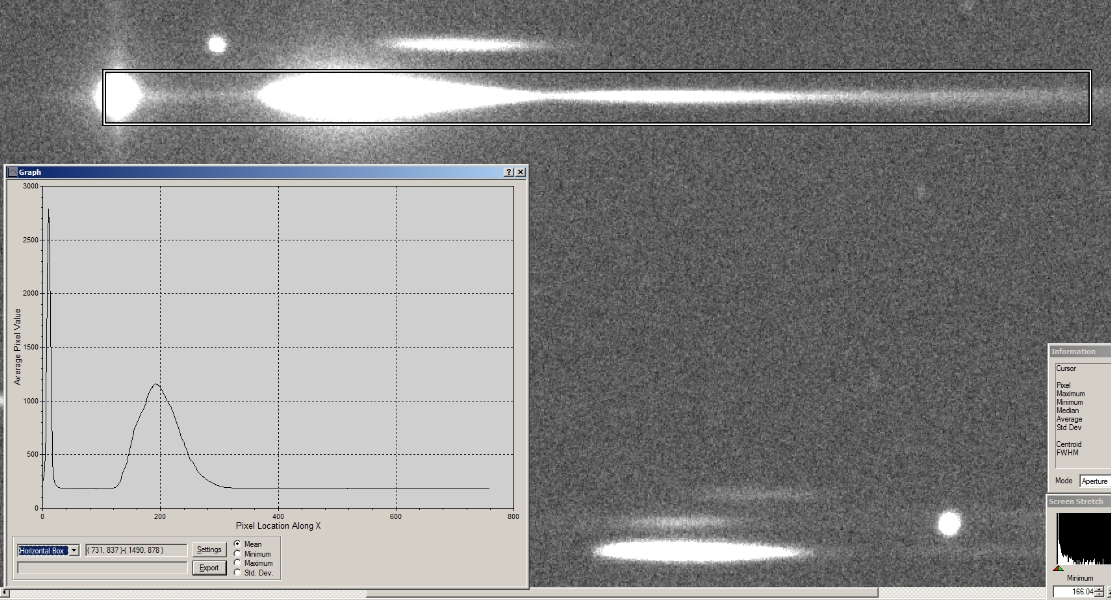
Figure 1. Horizontal box photometry of spectrum, extending from zeroth-order star-like image through the 1st-order spectrum and including most of the 2nd-order spectrum.

The csv-file produced from the box photometry tool is imported to a spreadsheet which I have designed for analysis of the SA-100 data. A baseline is created that can be adjusted by the user for offset, slope and 2-nd-order pixel offset, height and width (Fig. 2). The 2nd-order baseline component is a re-scaled version of the 1st-order spectrum, which is adjusted for intensity rescaling, pixel location offset and width (typically 1.47 times wider).


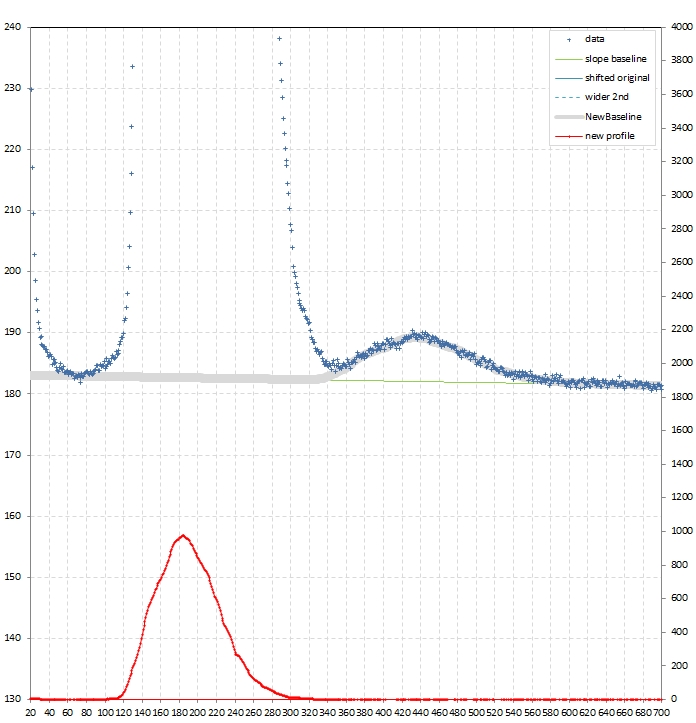
Figure 2. Baseline (thick gray trace) adjusted by user for intensity offset and slope. A version of the 1st-order spectrum is shifted to a 2nd-order pixel location; it is re-scaled and also widened by a factor ~ 1.48. The red trace at the bottom is what is left after subtracting the user-adjusted baseline.


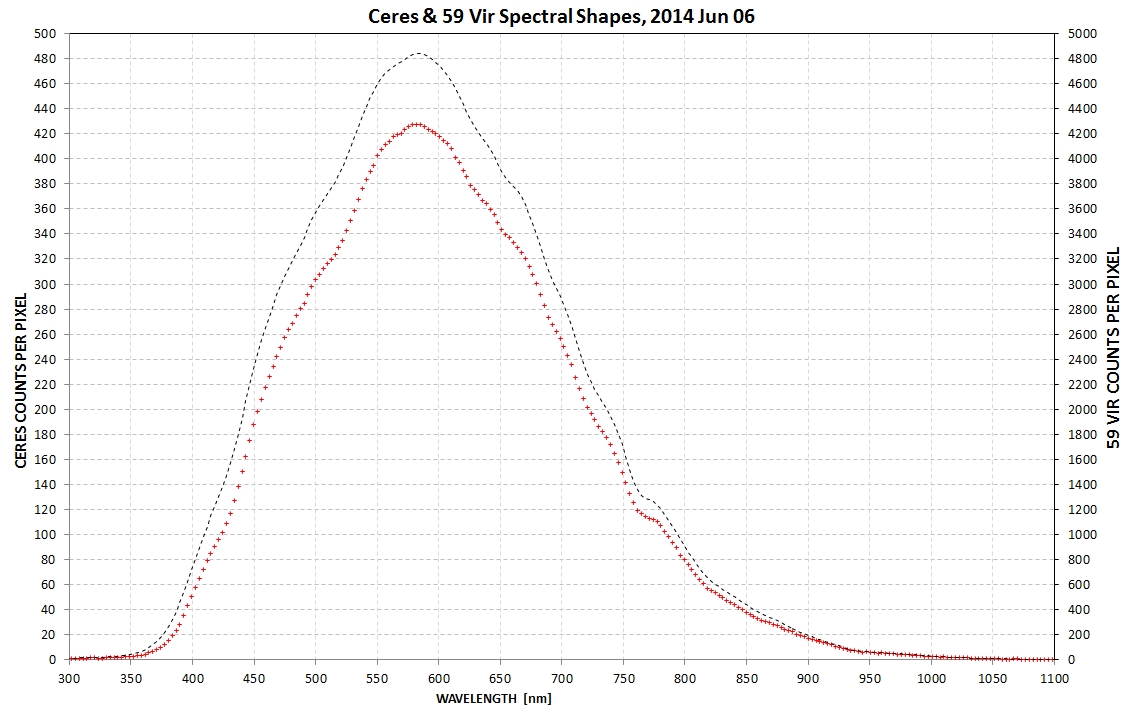
Figure 3. An observed spectrum of Ceres and standard star 59 Vir. Note the telluric oxygen absorption feature at 763 nm, and the very low intensity beyond ~1000 nm.

This figure illustrates the importance of carefully establishing a baseline for both the standard star and Ceres. It also can be used to visualize the errors that can occur if either has an incorrectly shifted wavelength adjustment (which is done manually for each spectrum, as described below).

Calibration of the pixel value to wavelength is accomplished using a star with many known absorption lines. Gamma Ursa Majoris (GUMa) is a A0V star which is ideal for this purpose (Fig. 4).


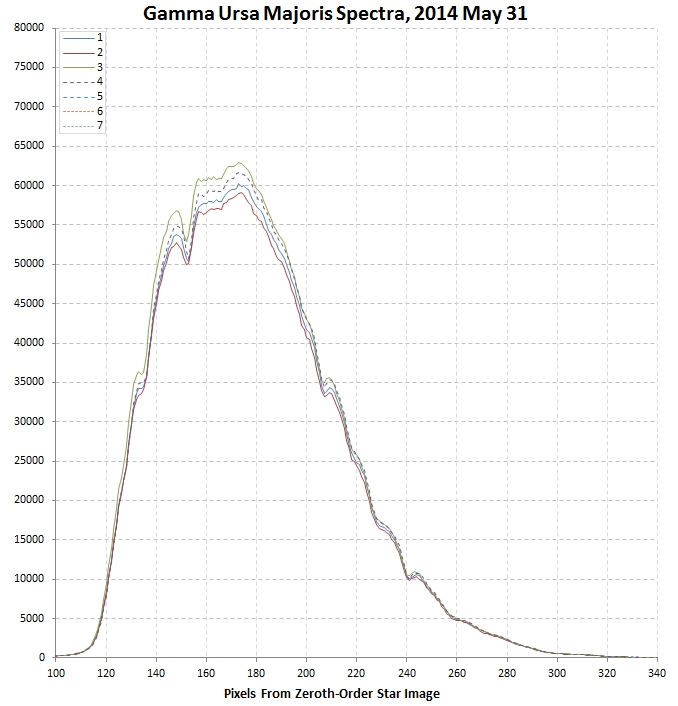
Figure 4. Four spectra of Gamma Ursa Majoris, showing several Balmer lines and some telluric (atmospheric) absorption features.

To see the absorption lines better I have created a "spectral structure" plot, using "intensity / smoothed intensity" (Fig. 5).


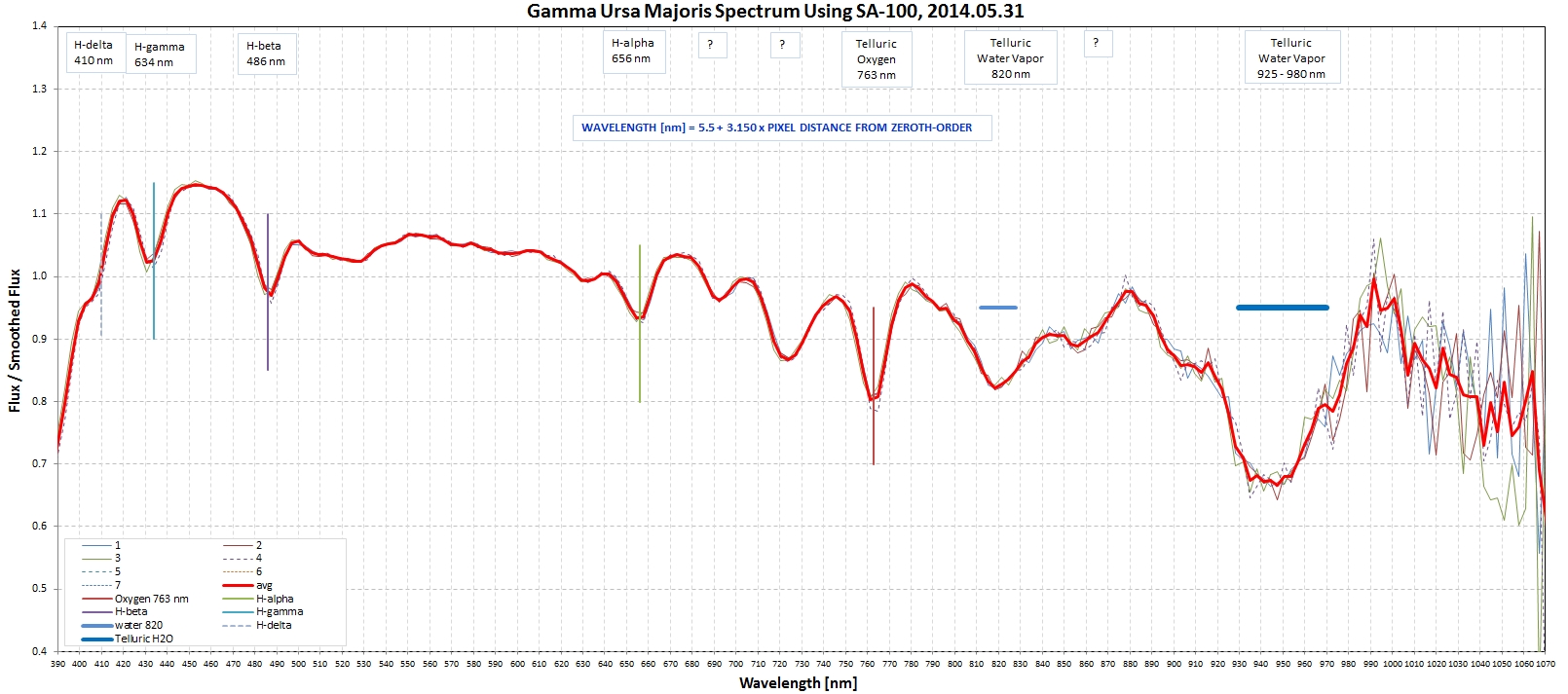
Figure 5. Gamma UMa "spectral structure" (intensity / smoothed intensity) used to establish the pixel to wavelength conversion equation.

Provided image scale doesn't change the equation for converting "pixels from zeroth-order location" to wavelength should be the same throughout an observing session, and from night-to-night. However, I found it convenient to use the telluric oxygen absorption feature at 763 nm for providing a final wavelength shift adjustment. Since this absorption feature is produced by the atmosphere it is present in every spectrum. Notice that the complex of water vapor absorption lines in the 930 to 990 nm region can mimic the 1 micron pyroxene Band I with a minimum at between 920 and 945 nm.

For an observing session I process all the 59 Vir (sun-like secondary standard star) images to produce a set of spectra with a spacing of ~ one hour. The first and last observations are always of this star, which assures that any changes in atmospheric extinction can be modeled for use with Ceres. The atmospheric extinction model has a resolution of one pixel's worth of wavelength (3.2 nm), and it consists of two components: an overall extinction for the night and a table of departures versus UT. I don't determine all of these parameters for each 3.2 nm interval; rather, I create "pseudo filter bands" by averaging over the FC bandpasses, and for each of these bands I plot log(Intensity) vs. air mass and "departure vs UT" (where "departure" is a visual reading of plotted difference from the air mass fit at 3 UT times), as shown in Fig. 6.
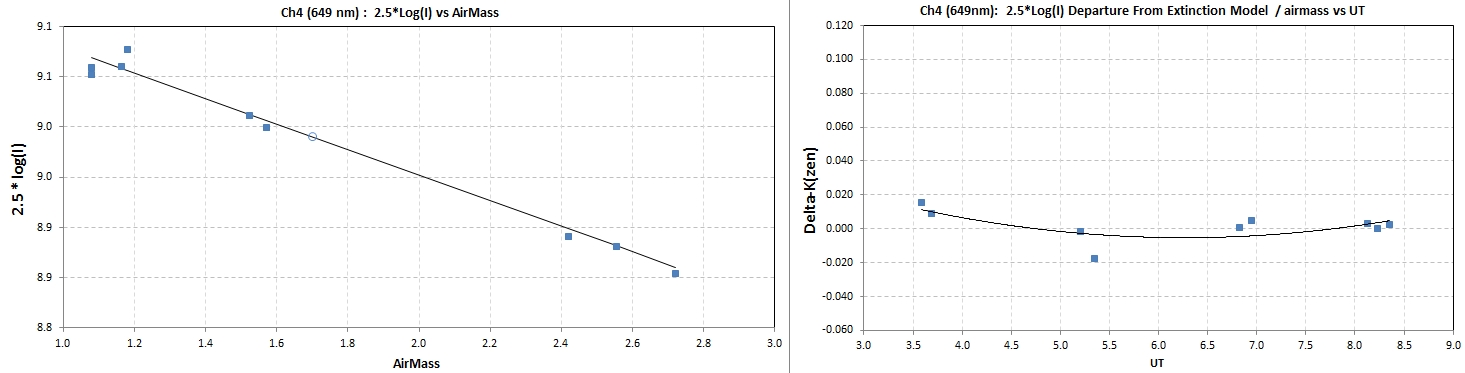  Figure 6. Calibration star (59 Vir) "pseudo FC band #6" log(Intensity) vs air mass with a simple atmospheric extinction fit (left) and plot of departures of panel a data vs. UT.

In the above figure the slope of 2.5*Log(Intensity) vs. air mass was fit using an atmospheric model constrained to have physically reasonable values for Rayleigh scattering, ozone absorption, aerosol scattering and water vapor absorption. The user can adjust a multiplier for each of these for extinction components subject to the a priori constraints. A Bayesian procedure could have been used but was not considered necessary at this early stage in assessing the SA-100.

After completing the calibration star reduction the Ceres image sets are grouped and median combined, etc, similar in manner to the procedure used for the calibration star. Groups of ~30 stars are typically "loaded" into MaxIm DL for review, and a PSF FWHM criterion is chosen for deleting images with poor "seeing" or tracking. Typically, 1/2 to 2/3 of the group is accepted for median combining (after Ceres "star alignment"). The horizontal box photometry file is imported to the spreadsheet, and baseline subtraction is performed in the same manner as for the calibration star - whose results reside in a special place for comparison with Ceres. After each median combined image photometry is processed the baseline subtracted counts spectrum is copied to a spreadsheet page for additional processing. The Ceres counts spectrum is divided by a version of the calibration star counts spectrum that the extinction model predicts would have been observed at the Ceres air mass and UT. This ratio is multiplied by the ratio "sun's flux / calibration star flux" versus wavelength. The result of this is a "Ceres flux / sun's flux" spectrum, which can be converted to geometric albedo using the standard parameters (r, d R, G). I've chosen the G vs wavelength result that I obtained using FC filters (fitted with a polynomial), shown as Fig 7.


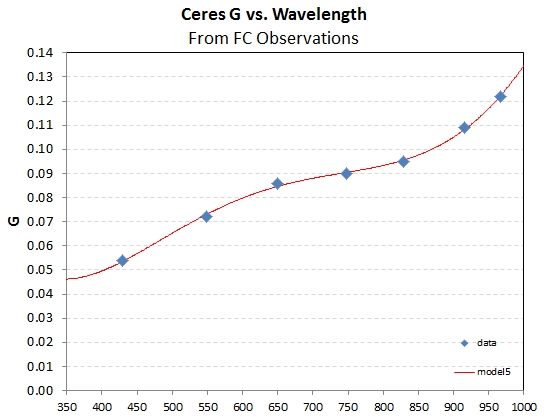
Figure 7. Phase effect parameter G versus wavelength based on FC filters for April and May, 2014.

Each image group leads to a spectrum, as shown in Fig. 8.


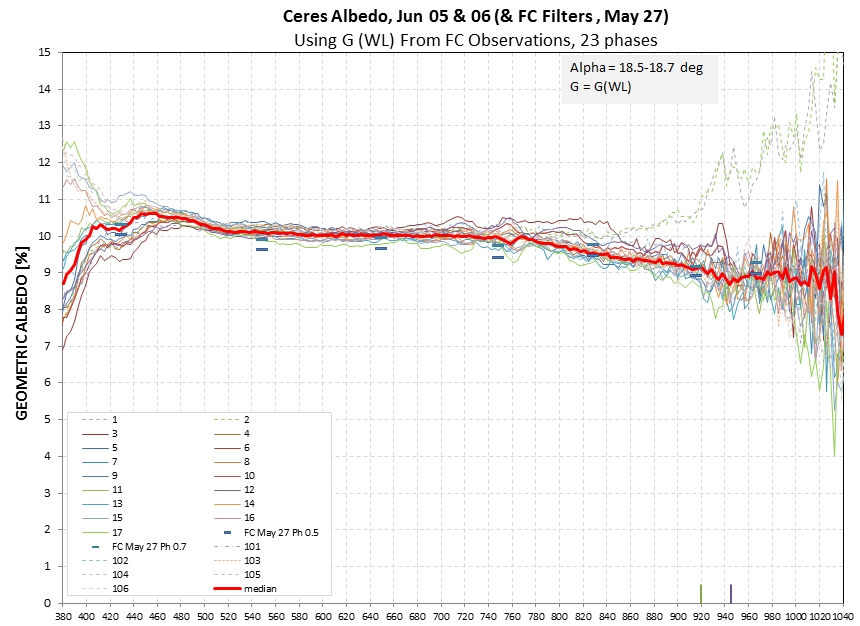
Figure 8. Spectra for 23 image groups, with rotation phases ranging from 0.13 to 0.64 (using an ephemeris where rotation phase is zero at JD = 2456736.73). Note the pairs of horizontal symbols at the FC wavelengths, which are measure geometric albedo for May 27.

Several results can be taken from this figure. First, the overall geometric albedo using the SA-100 is the same as for the FC filters. This is gratifying because completely different observing and reduction procedures are used for the two methods. This is the only positive result. The rest are negative!

At the short and long ends of the spectrum there are wild variations of albedo. At the long end two problems exist: 1) the spectra are noisy, and 2) there is a systematic problem with two traces. These two traces were made when a nearby star was producing a spectrum that overlay the Ceres spectrum. Refer back to Fig. 1 to see this star, which was moving with respect to Ceres in a manner that placed them at the same declination when the two outlier Ceres spectra were obtained. I note that a slit spectrograph would not have this problem.  The noisiness is cased by the instrumental response function going to zero at ~ 1100 nm, caused by corrector plate transmission, focal reducer lens transmission, SA grating transmission and CCD QE.

At the short wavelength end of the spectrum there is also a problem with instrumental response function, but the sun's spectrum also falls off fast with wavelength in this region. I think baseline fittings are difficult here because the zeroth-order PSF overlaps the short wavelength end of the 1st-order spectral region (refer to Fig. 2 to see this). The wild variations at wavelengths below ~ 460 nm may be caused by 1) weak solar flux combined with an uncertain baseline fitting, 2) steep decline of solar flux with decreasing wavelength combined with errors in aligning Ceres spectra with the average 59 Vir standard star spectrum.

The spectral region 460 to 680 nm is "well-behaved," and from 680 nm to ~ 920 nm most spectra agree with each other. The geometric albedo at 548 nm, for example (an FC band), has internal consistency that can be accounted for if each value has SE = 0.07 (based on neighbor differences). To use a specific example, at phase 0.478 the 548 nm SA-based geometric albedo = 10.01 ± 0.07 %, where the stated SE is the stochastic component. The systematic component of uncertainty is more difficult to estimate. This is comparable to the FC-based geometric albedo stochastic component; so for this band it should be possible to construct a phase-folded geometric albedo light curve, as in Fig. 9, below.


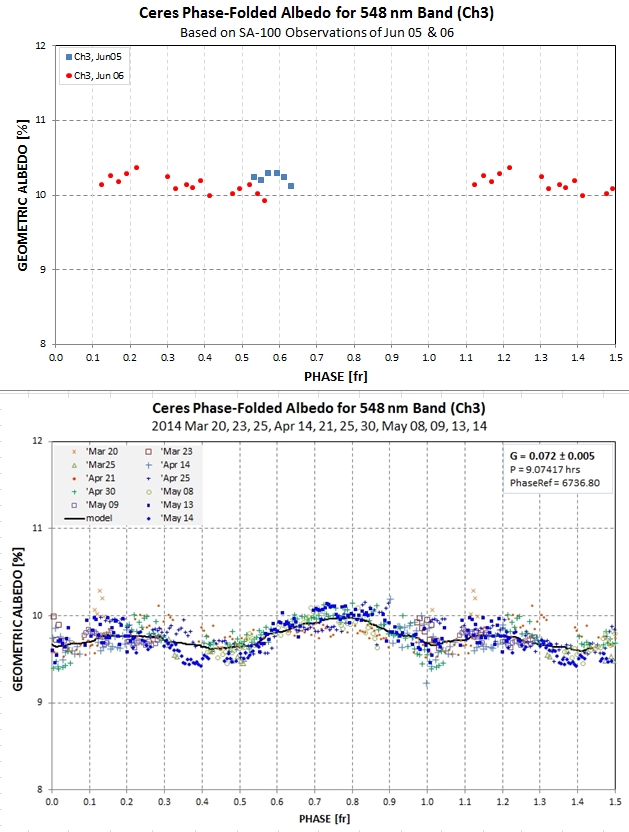
Figure 9. Phase-folded geometric albedo based on SA-100 observations (top) and FC filters (bottom).

The SA-100 phase-folded geometric albedo plot is compatible with the corresponding plot based on FC filters provided allowance is allowed for a G adjustment (since SA gives 10.15% vs FC's 9.75%). There is insufficient data to verify similarity of structure with rotation.

The one unique value in the SA-100 observations of Ceres, over the FC counterparts, is more spatial resolution. Referring to Fig. 10, below, the Band I feature is present, and possibly useful for assessing mineralogy.  However, the data in this region is so noisy that this use for the SA100 data is questionable.


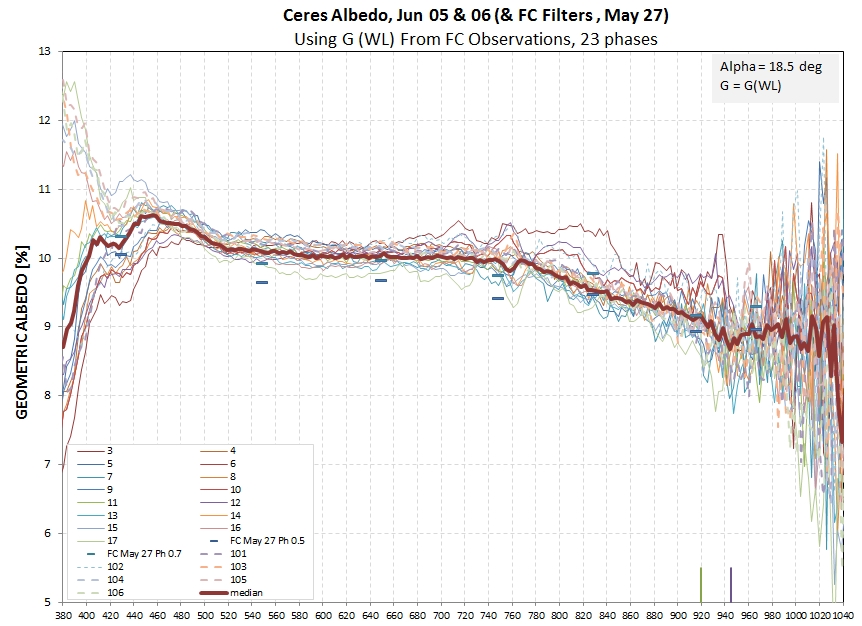
Figure 10. Plot of "median" spectrum of each geometric albedo plot for Jun 05 & 06, showing an un-useable "Band I" feature with a minimum at ~ 940 nm.

A small "Band I" feature is present, but the noisiness of even the median spectrum renders it essentially useless. Data quality in this region is affected by the water vapor absorption feature at the same wavelength region.

SA-100 Limitations

Consider the spectrum of Ceres as observed after instrumental losses caused by the atmosphere, corrector plate transmission, focal reducer transmission, SA-100 grating transmission and CCD QE.


Repeat of Figure 3. An observed spectrum of Ceres and standard star 59 Vir. Note the telluric oxygen absorption feature at 763 nm, and the very low intensity beyond ~1000 nm.

At the long wavelength end measured flux is so low that small changes in baseline fitting, for either Ceres or the standard star, can produce large changes in flux ratio. At the short wavelength end small changes in adopted wavelength shift (using the 763 nm telluric absorption feature) can produce large changes in flux ratio. It's my assessment that these two factors are the principal explanations for the large variations in geometric albedo (exhibited in Fig.'s 8 and 10). Another problem with using the SA-100 is something all transmission gratings must deal with: because transmission gratings don't use a slit the spectrum is superimposed upon a background of stars, as well as the spectra of those stars. Even when this problem is not obvious, as happened to cause the two outlier spectra in Fig. 8, these problems are present at lower levels for most other spectra. Their effect will of course be more noticeable for regions where the Ceres spectrum is faint, which may be a significant contributor for the noisiness at the short and long wavelength ends of the spectrum. 

Some of these problems could be alleviated by improving the instrumental response function. My Meade telescope's Cassegrain corrector plate, and the focal reducer, contribute to reduced response at the wavelength extremes. These components would not be present in a reflective optics only configuration. My ST-10XME CCD's QE is "enhanced" at the blue end, but the red end QE response fall-off is due to fundamental properties of silicon physics. Instrumental system response can be estimated from the ratio of a star's measured counts spectrum to it's actual flux spectrum, with an adjustment that produces a value at mid-wavelengths that can be calculated from documented performance specifications.  This is shown in the next figure.


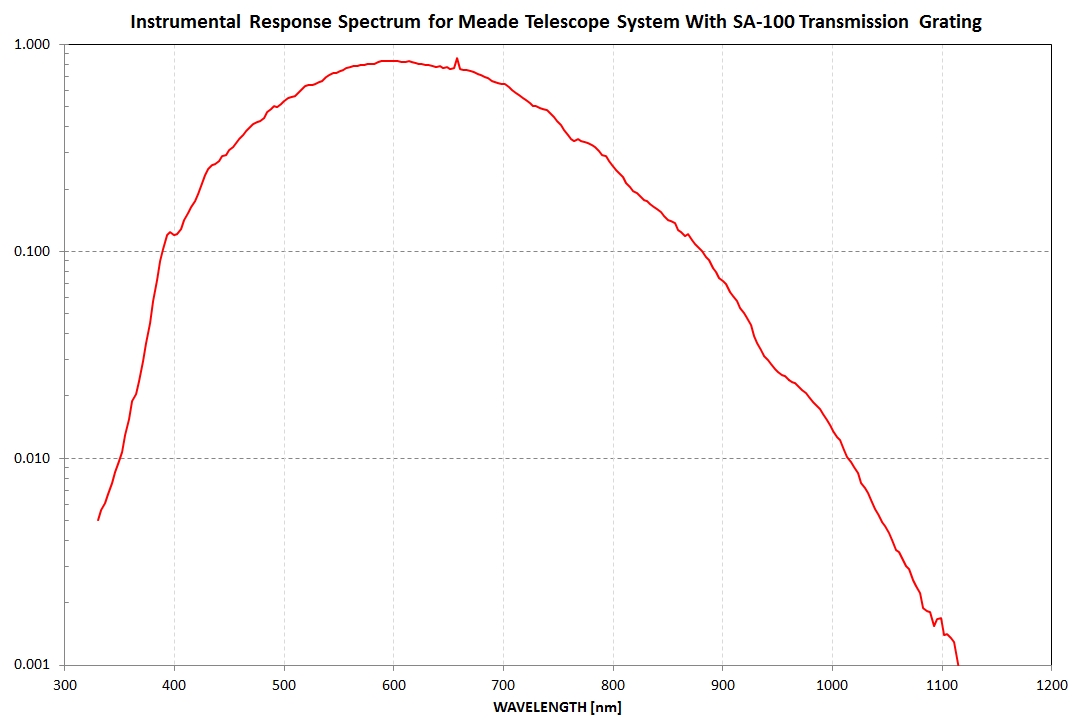
Figure 11. Estimated "instrument system response function" for my Meade telescope, with focal reducer, SA-100 and ST-10XME CCD. (The feature at 763 nm is due to the way this trace was produced: ratio of measured spectrum to known flux spectrum, adjusted at ~ 600 nm to be ~ 0.90).

The "instrumental response function" is > 50% from 480 nm to 780 nm, and the geometric albedo results are "well behaved" in that region. Clearly, one way to improve results with the SA-100 is to improve instrumental response by reducing transmission losses at the short and long wavelengths (i.e., using a reflective-only telescope system).

All-sky photometry with filters is less affected by a falling-off response function. This is due to several factors, but one is the fact that the spectral response function is not subject to user adjustments (meant to overcome changes in image scale as well as not knowing the exact location of the zero-order image due to PSF distortions and saturation). Another factor favoring filters where the response function is low is not having to rely upon user adjustments of a spectrum baseline. Finally, a filter system is not affected by order-overlap, which requires subjective modeling for the transmission grating observations.

Based on observations of asteroid BL86 (V = 9.5) and 2011 UW158 (V = 15.5) I can estimate the region in wavelength/magnitude space where SA1-00 observations are feasible with a 14" telsecope.


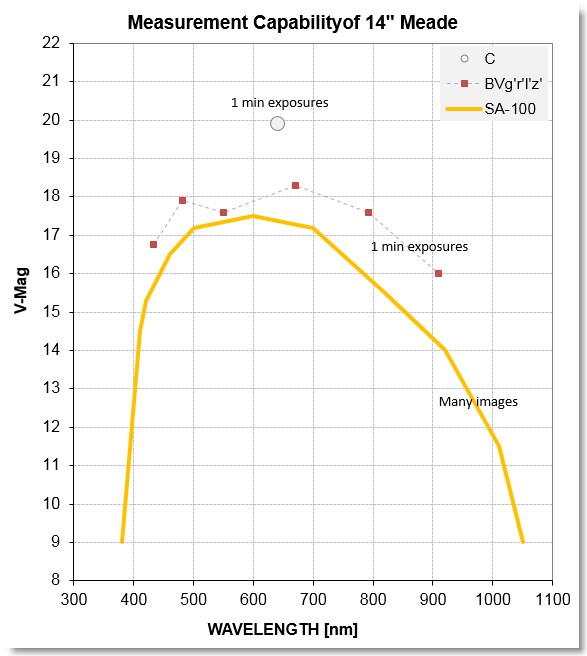
Figure 12. Measurement capability region for 14" telescope with SA-100 (yellow trace), assuming use of star subtraction, asteroid alignment and median combining of many images. For comparison, limiting magnitudes are shown for Clear and BVg'r'i'z' filters (60 second exposures, SNR = 3, 2.3 "arc FWHM).

To illustrate use of this figure, it is possible to observe the spectrum of an asteroid from 400 to 950 nm when it is at V-mag = 13.0.

In Conclusion

After taking my time trying to do the best possible job of processing SA-100 images of Ceres and a nearby calibration star, and because of the additional precautions I've incorporated for the SA-100 reduction I now can state that the SA-100 reduction process is more work than the FC reduction process. I think the SA-100 geometric albedo quality is slightly inferior to the FC albedo quality at the shortest and longest wavelengths, and I propose discontinuing observations with the SA-100 and returning to use of the FC filters.

Links

    Star Analyzer home page
    Master list of B. Gary web sites 


                ________________________________________________________________

This site opened:  2014.06.08.  Webmaster:  Bruce L. Gary