Recall from the first chapter our imaginary half-space of a blackbody material at a uniform temperature throughout, which shares the universe with a vacuum half-space. Photons are emitted by the material at the rate specified by the Planck blackbody equation. If this initial condition could be set up and then left alone, the material would cool from the lost energy of emitted photons. After all, it is the kinetic energy of particles that generates blackbody thermal radiation.
Let's alter the thought experiment by introducing a small blackbody test object somewhere in the vacuum half-space. Let's also expand the material half-space to enclose the object. In other words, the material at temperature Tu (temperature of the universe) fills the universe except for a cavity, at the center of which is our test object.
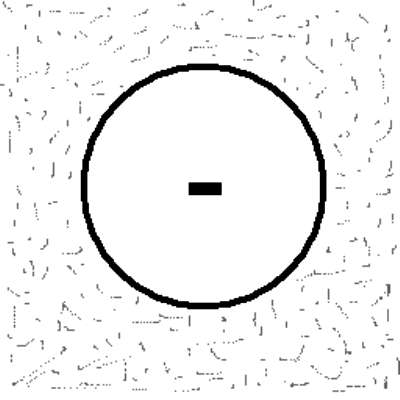
Figure 1. Universe, at temperature Tu, surrounding a test object at the center of a cavity.
I will now try to convince you that the temperature of the test object will eventually become equal to the temperature of the rest of the universe, Tu, regardless of the test object's initial temperature.
If the small blackbody test object starts out at 0 K it will be warmed by the photons it absorbs (radiated by the surrounding universe). After it acquires a non-zero temperature it too will begin radiating photons. The warmer it becomes the more photons it radiates. The total amount of energy it radiates per second is given by the Stefan-Boltzmann law (described in the previous chapter). When the temperature of a surface element of the test object is at the same temperature as the universe then the test object's unit surface will be radiating to a hemisphere the same power that it absorbs from the universe. The exchange of photons will be equal, on average,
for each wavelength interval. (I don't want to get into solid angles to convince you of this, so take my word for it; at least it's intuitively believable.)
The next step is to imagine that we can arrange a set of perfectly reflecting mirrors so that the test object is exposed to just one part of the universe. The reverse is true, that the photons emitted by the test object are reflected by the same mirrors and directed to the same part of the universe that radiates to it. For this case the test object doesn't "know about" any part of the universe not seen using the mirrors. And those other parts of the universe don't "know about" the test object. I am now going to ask you to believe that the test object will assume the temperature of that part of the universe that it "knows about." This is credible since the part of the universe to which the object radiates is the same part of the universe that radiates to the object.
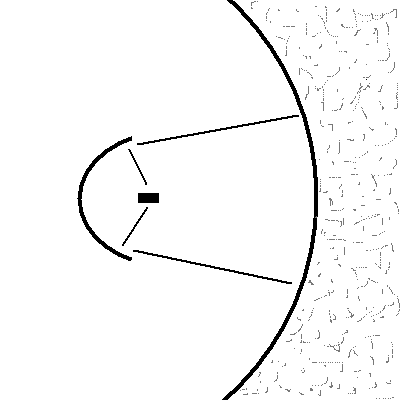
Figure 2. Object at focus of parabolic mirror with view of only part of the universe.
Now think of this object as an ordinary electronic "resistor" that is located at the vertex of a parabolic telescope. The resistor is enclosed in such a way that all it "sees" is the parabolic mirror, and since this parabolic mirror is a perfect reflector, the resistor only "sees" that part of the universe that the telescope is pointed at. If the telescope is pointed at a part of the universe that is at temperature Tx, then the resistor will be heated to temperature Tx also. We call a resistor in this configuration a bolometer (since photons of all wavelengths are included in this thought experiment). We measure the temperature of the resistor in order to measure the temperature of a part of the universe to which the telescope is pointed.
Now, suppose that the resistor has a filter in front of it. The filter passes photons within a certain wavelength band. If this wavelength band is fixed for a series of measurements, and if the wavelength band is at a long enough wavelength such that the number of photons is proportional to temperature of the object viewed by the telescope, then we have a way of comparing the temperature of different views. (The previous chapter showed that when the wavelength is longer than ~1 mm we can assume that the number of photons is proportional to temperature.) With this set-up we can point the telescope to an object of known temperature, then to a part of the sky of unknown temperature, and use the two readings (proportional to photons per second) to deduce the temperature of the unknown part of the universe. Of course, I've assumed that the resistor can change temperature faster than the time between readings.
The clever reader will wonder about the filter emitting photons to the resister, which it will, so the above thought experiment should really be modified slightly. Point the telescope reception pattern to two parts of the universe that are at two different, but known, temperatures (keeping the filter at a constant temperature). Then the reading for an unknown part of the universe can be converted to physical temperature by interpolation.
Note the fact that the detector (the resistor whose temperature is measured) is not in contact with the object whose temperature is being measured. The seems like some kind of "action at a distance" since there's no need to bring the detector into contact with the thing being measured. The part of the universe being measured can be a part of the moon, a distant planetary atmosphere, or even a human hand placed in front of the telescope. Indeed, I've actually performed crude calibrations of microwave radiometers by placing my hand in front of the radiometer's small aperture antenna and assuming the system should be registering a temperature equal to my hand's Kelvin temperature.
Microwave radiometers use a horn antenna to receive radio photons from a distant object. The larger the aperture of the horn antenna, the smaller is the patch of sky that is sensed. Photons from other directions aren't able to enter the horn antenna, so this limits the solid angle that defines what part of the universe is being measured. Sometimes the horn antenna "illuminates" a parabolic reflector, which leads to an even smaller patch of the sky being sensed. The reception pattern of the radiometer is therefore determined by the aperture of the horn antenna, or by the diameter of the parabolic reflctor if it is intercepting a horn antenna's pattern. (Notice that I'm writing as if the horn antenna is radiating, which it is, strictly speaking; this "dual property" of a horn antenna radiating as well as receiving is commonly used as a tool in understanding the properties of radio telescopes.)
Blackbody "targets" are used to calibrate the radiometer's output. A radiometer really isn't a bolometer, as implied above, but it ends up performing a similar function. The functional difference is that the radiometer "counts photons" within a specified range of wavelengths instead of across all wavelengths. That's a reason we can't simply measure the temperature of a sensor, like the resistor in the earlier examples. So we have to perform a clibration by looking at emissive blackbody objects of known temperature that are larger than the reception pattern of the antenna horn (or antenna and reflector combination). We call these emissive blackbody objects "calibration targets." These calibration targets are regulated at fixed temperatures and they are constructed to have an emissivity as close to 100% as possible. It is desireable to use calibration targets at temperatures that straddle the temperature of the unknown object.
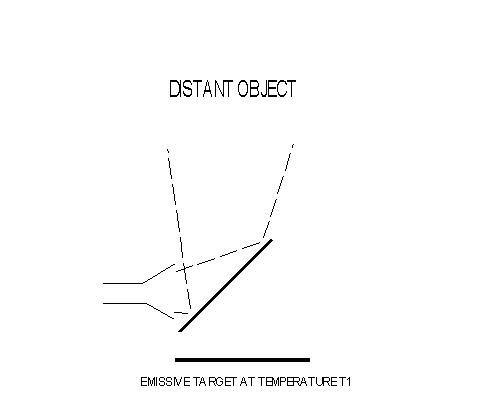
Figure 3. A horn antenna views photons from a distant object when a mirror is oriented for a view of the distant object. When the mirror is rotated for a different view, such as a calibration target at the bottom of this figure, the horn antenna delivers photons to a detector that allows for the association of one counting rate with a known temperature (T1, as shown). A second target (not shown) can be used to associate a second counting rate with a second temperature (such as T2).
This is the way a microwave radiometer can be calibrated for converting the output when viewing a distant target to a temperature based on readings of two emissive (blackbody) targets of known temperature. The temperature derived in this way is referred to as "antenna temperature." We are assuming that the distant object completely fills the reception pattern of the horn antenna (or horn antenna and flat mirror, or horn antenna and parabolic reflector if that's the configuration being used). When this is true then the measured antenna temperature is equal to the temperature of the distant object. When the distant target does not completely fill the reception pattern we cannot say that the measured antenna temperature is equal to the distant target's physical temperature. For this situation we must consider the temperature of the other parts of the reception pattern view.
In the next chapter we will consider a few subtle effects, such as the one just described. Another subtle effect is when the MTP radiometer's "distant target" is the atmosphere within which the MTP is embedded. Also, the distant target may not be uniform in temperature in the distance direction. Finally, the distant target may not be completely emissive (it may be partly reflective, and therefore less than 100% emissive). Although this last situation is not common for the MTP, the others are common, and there are subtleties associated with them. These subtleties will be treated in the next chapter.
Note: "Antenna temperature" is sometimes used with a different definition than the one just described, as in "the planet's antenna temperature was converted to disk brightness temperature using the ratio of solid angles..." For MTP the definition presented in this chapter is the relevant one.
Go to Chapter #3 (next chapter)
This is Chapter 2
Return to Chapter #1 (previous chapter)
Return to Introduction
____________________________________________________________________