Microwave photons, like all photons, interact with matter. Whether solid, gaseous or plasma, matter causes photons to be absorbed, emitted or refracted. Emitted photons are either "thermal" in origin, or non-thermal (synchrotron, Cerenkov, laser, etc). Thermal photons are emitted with all energies (wavelengths), but their number varies with wavelength according to the Planck blackbody radiation equation.
Consider a thick slab of material (a semi-infinitie "half-space"), having a uniform temperature throughout, that does not reflect photons incident upon it. Imagine further that there are no photons incident upon it because it shares a universe consisting of vacuum for the other semi-infinite half-space. How many photons will be radiated by this surface per second, per square micron?
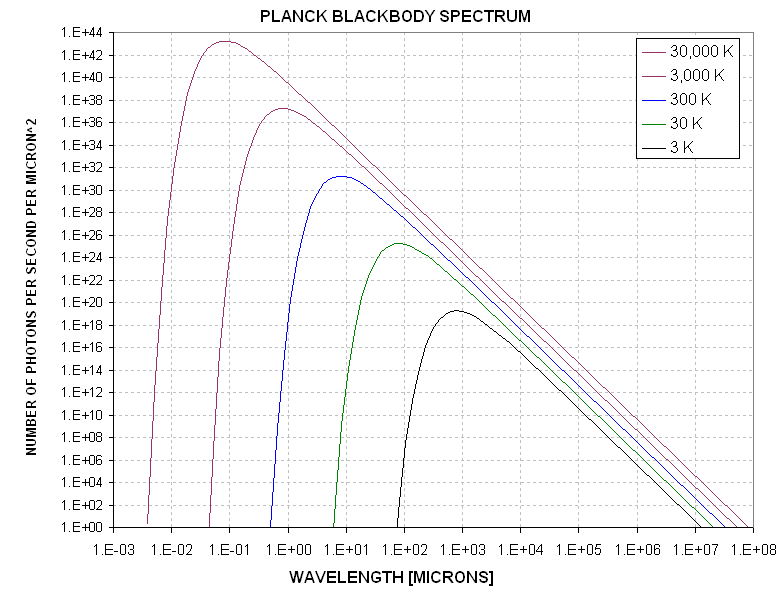
Figure 1. Blackbody photon count (per second, per square micron, per unit of wavelength) for various temperatures.
This figure shows the blackbody photon emission for a range of temperatures corresponding to a very hot star surface (30,000 K), a cool star surface (3000K), a typical Earth surface ambient temperature (300 K), a cooled radiomter detector (30 K), and the coldest anything in the universe can reach (in a natural setting), the cosmic background level of 3 K. It may be difficult to see in this figure, but longward of a certain wavelength, for each temperature, the number of photons radiated is proportional to the temperature. For all wavelengths longer than 1000 microns (1 mm) the number of photons is proportional to temperature, regardless of the material's temperature (given that temperature will never be colder than 3 K). It is also interesting to note that the bottom level corrresponds to there being only a 50% chance that in one second a photon will be emitted. It is therefore slightly misleading to state that every material emits photons at all wavelengths, since for every temperature there is a wavelength shotward of which it can be said that at no time duing the age of the universe is it likely that a photon will have been radiated.
For present purposes it is only necessary to note that for the wavelengths of a microwave radiometer, and for temperatures typical of the earth's atmosphere (e.g., 300 K), the number of photons emitted is proportional to temperature.
As an aside, not necessary for an understanding of the MTP, the above graph is usually presented as a plot of energy radiated (per unit wavelength, per unit area, per second). If a spectrum of energy radiated is integrated throughout all wavelengths, the area enclosed (the total energy radiated) is propotional to T4. This is called the Stefan-Boltzmann law: E = constant * T4. I'll refer to this in the next chapter.
Go to Chapter #2 (next chapter)
This is Chapter 1
Return to Introduction
____________________________________________________________________