This web page describes observations of Asteroid "15146 Halpov" made with my 14-inch telescopes. It's the first asteroid I've observed that has a rotational axis tipped about 90 degrees from the normal perpendicualr to the orbit plane. It will therefore be useful in exploring methods for characterizing the axis orientation and rotation period.

Introduction

This is one of two asteroids named for astronomer Hal Povenmire (the other one is canmed "12753 Povenmire" which is described at 12753). In 2003 I spread the word to local amateur astronomers that I was interested in starting an asteroid project, and when word of this reached Hal Povenmire he immediately suggested that I try observing his 12753 asteroid, which had eluded others. When 15146 was named for him a year later I added this one to my list of challenging asteroids. It's more of a challenge because of its smaller size and additional faintness. At a typical opposition it has a V-magnitude of about 18.0, which is 1.3 magnitudes fainter than 12753 (i.e., half as bright).

The following entries are presented in the order: "most recent at the top." Some of the flavor for how my project has evolved is more difficult to follow this way, but that's how I prefer to present all my projects.

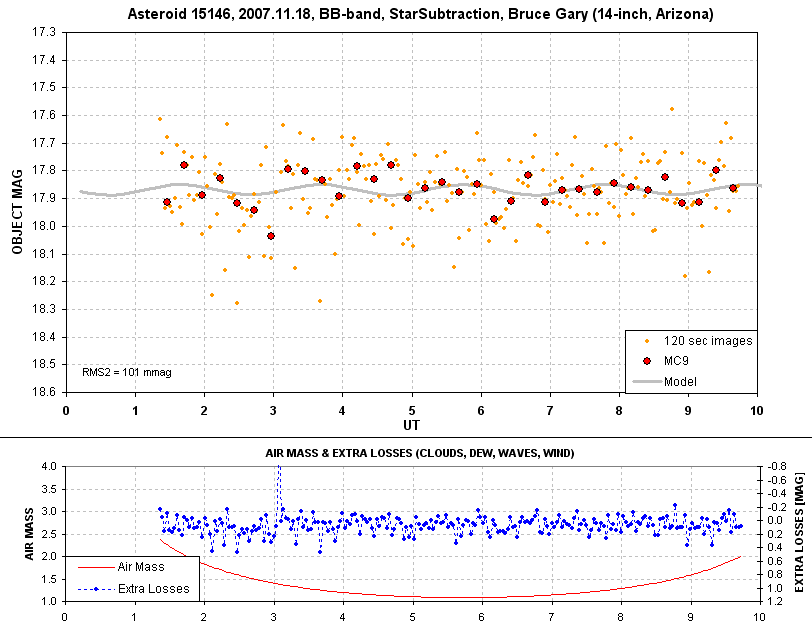
Rotation Light Curve: 2007.11.18

After 2 1/2 years I decided to refine the period of 15146, and maybe determine if it rotates prograde or retrograde. I was surprised to find that the rotation light curve amplitude was smaller than expected by more than a factor 10! This could only be accounted for if the rotation axis was now pointed to earth, whereas 2.5 years ago it was at an angle closer to 90 degrees different. This is an exciting finding! It's the first asteroid I've observed that has its rotation axis tipped about 90 degrees from "normal." Here's the recent rotation light curve.

The fitted sinusoid has an amplitude of 0.01 magnitude (half of peak-to-peak). Because the amplitude is so small the phase is poorly established, and cannot be used for refining the rotation period.

If the rotation light curve is asymmetric it may be possible to distinguish from the two orintation possibilities. In other words, using the right-hand rule, is the axis now pointed toward or away from earth? This will be one of my future objectives for future oppositions.

Rotation Light Curve: 2005.03.16

During a 3.5-hour observing session on March 16, 2005 UT, I observed the asteroid unfiltered. Two Landolt star fields were also observed this evening, and because the atmosphere was "photometric" it was possible to transfer the Landolt star field calibration to the asteroid star field. Details of the data analysis procedures are given below. The following graph shows the set of calibrated brightness measurements of the asteroid during the 3.5-hour observing session.

 
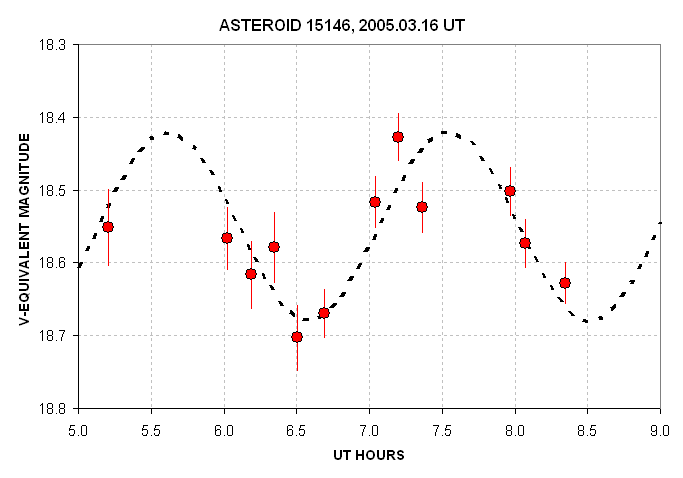
Figure 1. Rotation light curve for the asteroid using the following parameters: V-magnitude average = 18.55, rotation period = 3.86 hours, half-amplitude of rotation variation = 0.13 magnitude, phase of variation = 6.1 hours UT.

Each 3-minute exposure was calibrated (dark and flat) and groups of 3 images were median combined twice: once using the stars for alignment and once using the asteroid for alignment. The star-aligned median combined images was used to determine an aperture response correction meant to allow a small signal aperture flux measurement of the asteroid to be converted to what would be measured if a large signal aperture were used. This procedure allowed me to retain the high SNR of a small signal aperture measurement of the faint asteroid while converting the corrected flux to a magnitude based on large signal aperture flux measurements of a well-calibrated nearby reference star. Since the observations were made unfiltered it was necessary to employ a procedure for converting unfiltered flux to equivalent V-magnitude. This was done using the following equation: 

    C-mag = 21.25 - 2.5 * LOG (F / g) -0.13 * m + 0.30 * (B-V) +0.04 * m * (B-V),

where C-mag is equivalent V-magnitude, F = flux [counts], g = exposure time [seconds], m = air mass, and (B-V) is the B-V color a star/asteroid would have for its V-R color assuming the typical color/color relation. I have found this equation to exhibit an accuracy of ~0.03 magnitude.

The following image is a cropped version of the star field through which the asteroid moved during the March 16 observing session.

Figure 2. The arrow denotes the path of the asteroid during the 3.5-hour observing session. FOV = 10.3 x 10.9 'arc (27% areal crop); north is up, east is left. The total exposure time for this image is 120 minutes, and the limiting magnitude is 22.9.

The following animation shows the asteroid's motion during the 3.5-hour observing session.

Figure 3. Animation showing the asteroid's movement during the 3.5-hour March 16, 2005 observing session. FOV = 4.1 x 4.3 'arc. Stars have been "edited away" for frames where the asteroid is close to the star.

The asteroid's V-band and R-band magnitudes were measured (closely-spaced in time) on March 11, 2005 UT. On the same observing session three Landolt star fields were observed. The asteroid results are V-mag = 18.48 +/- 0.06 SE (stochastic) and R-mag = 18.17 +/- 0.05 SE(stochastic). The asteroid's V-R color = 0.31 +.- 0.08 SE(stochastic). If the asteroid's B-V and V-R colors behave in the same way as typical stars then the asteroid's B-V = 0.54 +/- 0.15. This color is similar to stars, which typically exhibit a B-V = 0.64. Thus, the asteroid might be slightly bluer than a typical star, although the uncertainty on it's color is large enough that it may actually be the same color as a typical star.

Notice that the V-magnitude value of 18.48 +/- 0.06 is compatible with the C-magnitudes (i.e., equivalent V-magnitude based on unfiltered measurements) plotted in Fig. 1. If we adopt the unfiltered C-magnitude of 18.55 then we can adjust the ephemeris value for H. Since the ephemeris was predicting a brightness of 18.19 for March 16, based on H = 13.8, we can suggest from these observations the following new value: H = 14.16 +/- 0.06. In other words, the asteroid is 0.36 +/- 0.06 magnitudes fainter than the ephemeris predictions.

The size and expected rotation period depend on the asteroid's albedo. There are three asteroid classifications to consider (for 96% of all asteroids). If it's a C-type (75% of asteroids) it will have an albedo of 2 to 6%, its diameter would be 8 to 14 km, and the expected rotation period would be 5 to 8 hours. If it's an S-type (16% of asteroids) it would have an albedo of 10 to 20%, its diameter would be 4.4 to 6.2 km, and the expected rotation period would be 4.8 to 6.3 hours. If it's a M-type (5% of asteroids) it would have an albedo of 10 to 18%, its diameter would be 4.6 to 6.2 km, and the expected rotation period would be 4.8 to 6.3 hours. Whatever type this asteroid is it can be called a fast rotater since its period is shorter than any of the above classification assumptions.

This site opened:  March 17, 2005.  Last Update:  December 05, 2007