Asteroid "2012 DA14"
Rotation Light Curve
Bruce L. Gary, Hereford Arizona
Observatory, 2013.02.18
ABSTRACT: During
the outbound part of the close flyby of asteroid "2012 DA14"
on 2013.02.16 I used a 14-inch Meade telescope configured
with a prime focus HyperStar lens to observe the asteroid's
r'-band brightness for 12 hours. The observations began 6.5
hours after closest approach, and the observing geometry was
constant (sun-target-observer angle) which is ideal for
determining a rotation light curve. The light curve is
complicated, with several (real) bumps, and the rotation
period on the outbound trajectory was ~ 9.1 hours.
The rotation light curve (below) appears to go from just
before a secondary minimum to just after it occurs again.
The primary minimum is 0.23 magnitudes fainter than the
secondary. This can be caused by the way the surface is
illuminated by the sun and also by possible shading. The
sun-target-observer (S-T-O) angle ranged from 75 to 81
degrees during the 10 hours that had useable data, so only
about half of the asteroid was illuminated by the sun.
Light curve showing the first 10 hours of a 12-hour
observing session. The magnitude scale is based on 196 stars
in 19 field of views that have calculated r'-band magnitudes
based on their J & K magnitudes.
1. Background
Asteroid "2012 DA14" was discovered in
2012.02.23 by observers at the Observatorio Astronomico de
la Sagra, in Granada, Spain. It orbits the sun with a semi-major
axis of 1.002 a.u., inclined to the ecliptic plane ~ 10
degrees and with a period of 368 days (until
passage by Earth in 2013). It's diameter is estimated to be ~ 50
meters. After the 2013 Earth flyby the period is estimated
to be 317 days. The 2013 flyby was from south to north, at a
distance from Earth's center of 23,600 miles (5.7 Earth radii).
Observers in North America had an observing window on the
2013.02.15/16 flyby starting on 2013.02.16, 0200 UT (7.6 hours
after closest approach) and extending until sunrise the
following morning (~ 12 UT). Dr. Lance Benner of Caltech's JPL
is planning radar observations with the Goldstone Tracking
Station (70-meter antenna) during Feb 16 - 20. Other radar
observations are planned for Arecibo Ionospheric Observatory,
MIT's Haystack antenna, the Allen Telescope Array (eavesdropping
on GTS signals), and Norway. Dr. Nicholas Moskovitz (MIT) heads
a large photometry observing project (KPNO's 2.1-meter telescope
and others) in search of a change in rotation period caused by
gravity gradient torques. Prior to closest encounter Dr.
Moskovitz measured a rotation period of ~ 6 hours using a
photometry-generated rotation light curve.
2. Hardware and Observing Procedure
Observations at the Hereford Arizona Observatory (HAO) began
2013.02.16, 02:00 UT and ended 12 hours later.

Figure 1. Hereford Arizona Observatory (HAO) consists of
two domes with Meade 14-inch and Celestron 11-inch telescopes
inside, that are controlled from an office using cables in buried
conduit.

Figure 2. Prime focus lens (Starizona's HyperStar) and
CCD camera (SBIG's ST-10XME) with 10-slot filter wheel.
A HyperStar prime focus lens (manufactured by Starizona) was used
with the Meade 14-inch telescope. An SBIG ST-10XME CCD camera and
filter wheel assembly is attached to the HyperStar lens. The focal
ratio is f/2.03, which provides an image scale of 1.95 "arc/pixel
and field-of-view (FOV) = 71 x 48 'arc.
Yes, the large filter wheel blocks light, but when the optics are
collimated and the primary mirror is focused the
point-spread-function (PSF) is very sharp and there's no obvious
evidence of some lost light. The PSF has a FWHM as small as 2.0
pixels (4.0 "arc) when properly focused. This compares with typical
PSF widths of 2.5 to 3.5 "arc when observing in Cassegrain
configuration (at my observing site). The small loss of PSF
sharpness is unimportant compared with the 7-fold increase in FOV
area.
MaxIm DL was used to control the various components of the
observatory: telescope, CCD, filter wheel, wireless focuser
(Starizona's MicroTouch) and dome. Control lines run through a
buried conduit, and AC power is provided by a separate buried
conduit.
A pattern of 19 FOV placements were used to observe the asteroid for
a 12-hour observing interval. Each FOV change was accomplished using
the MaxIm DL "Move telescope here" tool, which used about one minute
of observing time. If the telescope had been in the Cassegrain
configuration the number of FOV position changes would have been ~
50, and this would have reduced the time available for exposures.
This illustrates the importance of observing near-Earth-objects with
as large a FOV as possible, which underscores the importance of the
HyperStar configuration.
The choice of r'-band was motivated by two considerations: 1) an
expectation that the asteroid would be redder than a typical star,
and 2) the r' filter has the highest throughput of the entire set
BVRcIcg'r'i'z'. Only the Cb filter (clear with blue-blocking) has
greater throughput, but it suffered from image quality problems that
I didn't have time to diagnose.
A few hours before observations began calibration images were taken
using the r' filter. These consisted of bias (N=26), dark (N=20) and
flat (N=14).
The apparent motion of "2012 DA14" was fast at the beginning of the
observing period (~ 160 "arc/minute) and was much slower near the
end (~14 "arc/minute). Exposure times went from 3 seconds at the
beginning to 10 seconds during the second half of the observing
session. In the first several images the asteroid's PSF had an
oblong shape, ~ 8"arc in length, while the PSF quickly became
circular due to a slowing sky motion - as the image in Fig. 3
illustrates (taken ~ 10 minutes into observing).
A total of 2250 images were taken during the 12-hour observing
session, but due to focusing drift that occurred while I was
sleeping only the first 1910 images (10 hours) were useful.
3. Image Analysis and Light Curve Processing
Figure 3 is a typical single frame. The circular photometry
pattern shown is "twice" the size used for measurements. Photometry
measurements were made with a signal circle having an 8-pixel
radius, a 2-pixel gap, and an 8-pixel sky background annulus. This
choice meant that for a typical range of seeing (and tracking
quality) ~ 97 % of each star's flux was "captured" by photometry
measurements. The HyperStar produces essentially the same PSF over
the FOV, so for each image the capture fraction was the same for the
asteroid and all reference stars. This is an important requirement
for differential photometry because it means that capture fraction
can be different for each image without affecting the target's
instrumental magnitude.

Figure 3. Single frame at 02:10 UT showing "2012 DA14"
(circled) when r'-magnitude = 12.4 and SNR = 88. Limiting
magnitude for this 3-second exposure = 17.3 (for
r'-band). North up, east left, FOV = 71 x 48 'arc.
Approximately 15 to 20 "reference stars" were chosen for use for
each of the 19 FOVs. Stars close to saturation were avoided. MaxIm
DL's photometry tool allows for a moving target (to accommodate
asteroid observers). The moving target assumes straight line motion,
and sometimes when the asteroid moves close to a bright star the
program makes a tracking mistake. When this was noticed I divided
the FOV image set into subsets of 2 or 3, and this always led to
correct moving target tracking.
MaxIm DL allows for a visual inspection of each FOV's light curve
before recording to as CSV data file. None of the "reference stars"
showed variability. Quote marks are used for "reference stars"
because an artificial star was used as a single reference, and the
15 to 20 stars chosen as candidates for reference were assigned
"check star" status in the MaxIm DL photometry routine. This was
done because at this stage of analysis none of the stars
chosen as candidates for reference (the "check stars") had known r'
magnitudes. A CSV-format data file was recorded for each FOV.
The CSV files were imported to an Excel spreadsheet. The
instrumental magnitudes (referenced to an artificial star with
arbitrarily assigned magnitude) were adjusted for changing asteroid
range and plotted as a crude light curve (LC). Such a LC would be
valid only if atmospheric extinction were constant throughout the
observing session. Since "2012 DA14" was close to the north
celestial pole during the entire observing session all data were
confined to a small range of air masses (monotonically changing from
2.51 to 1.93), and if zenith extinction was constant then
atmospheric extinction for the asteroid would also be constant. The
resultant LC looked almost exactly like the figure in this web
page's abstract (repeated as Fig. 5).
The next analysis phase was to obtain r' magnitudes for some of the
reference stars in each of the 19 FOVs. Asteroid observers are
familiar with the Carlsberg Meridian Catalog (release 14), because
it includes r'-band magnitudes that are useful to r' ~14.5 for most
of the sky where asteroids are observed, from declination -40 to
+52. The north celestial pole region is without r' magnitude
coverage, but these stars have J, H and K magnitudes. I used the
standard SDSS magnitude catalog of Smith et al (2002) which contains
102 stars calibrated in bands u'g'r'i'z' and found a way to convert
J and K magnitudes to r' magnitude. As Fig. 4 shows, a 3rd order fit
of r'-J to J-K can be used with ~ 0.08 magnitude SE throughout a
large range of J-K star color. All of the candidate reference stars
in each of my 19 FOVs could be converted to r'-magnitude using a
simple conversion equation. This was done for an average of 10 stars
for each FOV, which assured a range of star colors (e.g., J-K) were
represented for each FOV. Each FOV's set of reference stars provided
internal consistency (after rejecting a few outlier stars, possible
variables) with a SE on the average of 0.015 magnitude. This
accuracy is ~ 1% of the asteroid's brightness variation, so the
offsets of data for one FOV to the next is expected to be
insignificant.
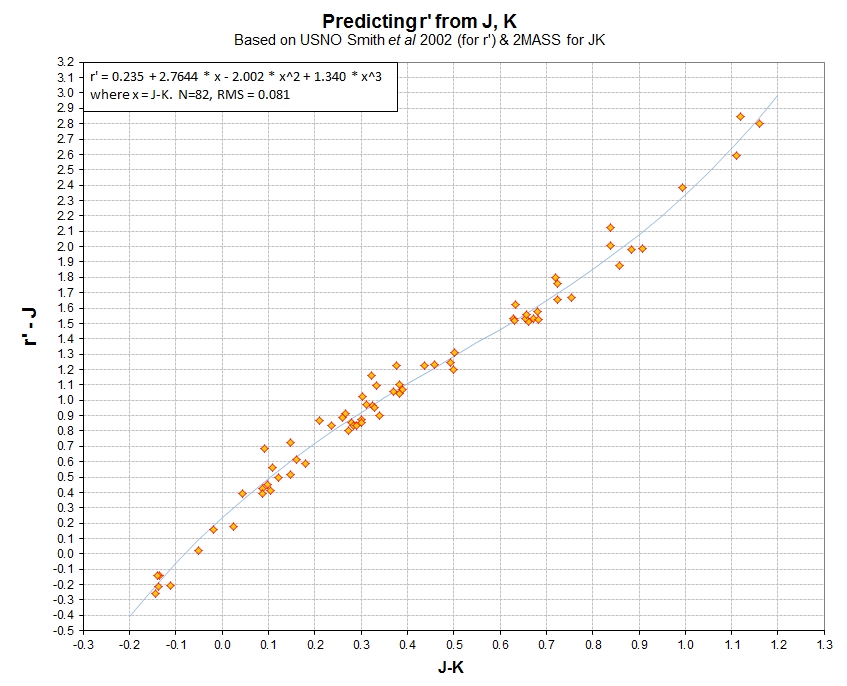
Figure 4. Color-color relationship for "r'-J" and
"J-K" that can be used to convert J and K magnitudes to
r'-magnitude.
When the candidate reference stars were assigned an r'-magnitude
they "became" reference stars. The resultant r'-magnitudes for one
FOV were verified using a traditional differential photometry
procedure, so it was not necessary to reprocess all image sets using
the traditional method. A total of 196 stars with r'-magnitude
calculated using the JK conversion equation were used for the 19
FOVs.
Measured r'-band brightness is plotted versus UT in Fig. 5. The
fading trend is caused by an increasing observer-target range. The
noisiest data after 11 UT is partly due to the asteroid's faintness
and also to a drifting focus error that was not noticed and
corrected (because I was asleep at the time).
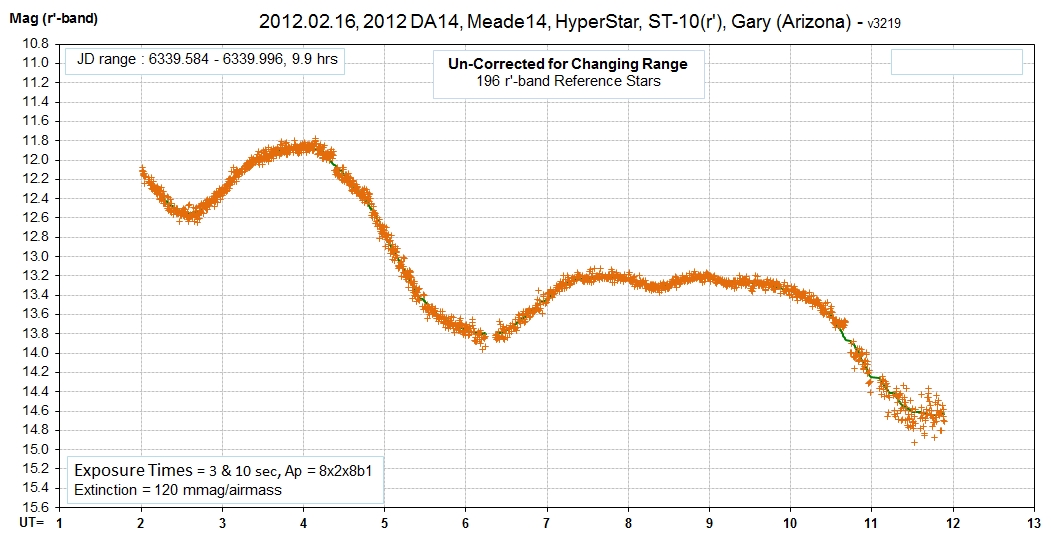
Figure 5. Light curve showing the first 10 hours
of a 12-hour observing session. The magnitude scale is based on
196 stars in 19 field of views that have calculated r'-band
magnitudes based on their J & K magnitudes. No
correction has been applied for the asteroid's changing
"observer-target" range.
The fading effect of increasing target-observer range was removed by
applying a third-order polynomial fit to the JPL ephemeris listing
of asteroid apparent magnitude. The final LC for the first 10 hours
of the observing session are shown in Fig. 6.
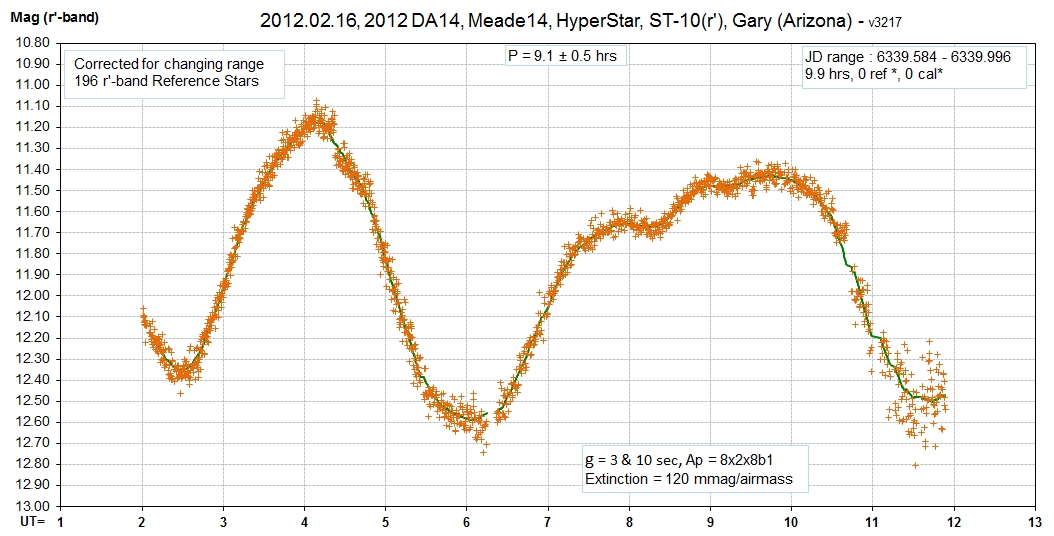
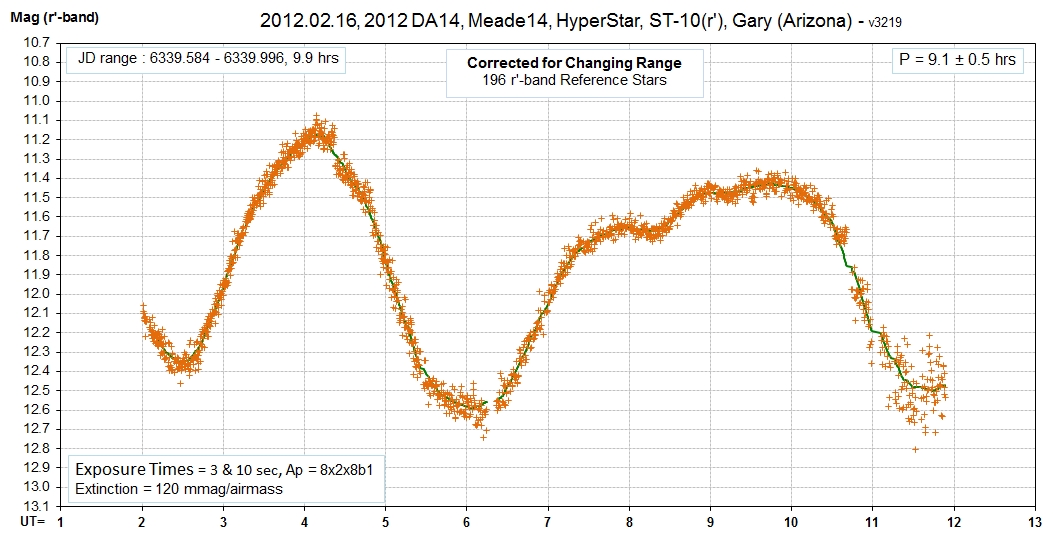
Figure 6. Light curve showing the first 10 hours
of a 12-hour observing session. The magnitude scale is based on
196 stars in 19 field of views that have calculated r'-band
magnitudes based on their J & K magnitudes.
The thick trace is a running average. A few outlier data points have
been deleted. Data past 12 UT are not worth processing.
Data file: link
4. Possible Interpretation of Light Curve Shape
Several features of this LC are noteworthy. 1) The primary
minimum is at 6.1 UT, and it is my interpretation that the minima at
2.45 UT and 11.6 UT are secondary minimum. If so, then the rotation
period is ~ 9.1 hours. 2) There's a magnitude difference between the
two secondary minima, but it may not be statistically significant
due to the noisiness of data past 11 UT. 3) The primary minimum is
0.23 magnitudes deeper than the secondary (ratio of 1.24). 4) the
shape of the brightest maximum is significantly different from the
shape of the fainter maximum. One is "pointed" and the other is
"bumpy flat." 5) The fainter maximum "bumps" are probably real since
they also appear in the LC produced without the use of reference
stars (instrumental magnitude vs. UT, assuming no atmospheric
extinction changes and adjusted for changing range). 6) The interval
between the secondary and primary minima is ~ 2.45 hours, whereas
the interval between the primary and secondary minima is 5.5 hours.
These intervals are in the ratio of ~ 2.2. This might be what would
be seen by a "rotating banana."
The rotation period of ~ 9.1 hours is ~50% greater than the
preliminary measurement of 6 hours by Moskvitz (private
communication). If the period difference is real then it would
constitute evidence for a change in rotation period caused by
gravity gradient torques, which is a major goal of the "2012 DA14"
photometry project led by Moskovitz.
5. References
Smith, J. Allyn, et al, 2009, AJ, 123,
2121-2144.
Related Links
JPL Radar Observing Plan: http://echo.jpl.nasa.gov/asteroids/2012DA14/2012DA14_planning.html
Dr. Moskovitz KPNO Observing Plan: http://www.noao.edu/news/2013/pr1302.php
Peter Birdwhistle (3.0 hr LC): http://peter-j95.blogspot.co.uk/2013/02/partial-lightcurve-for-2012-da14.html
Description of HAO: http://www.brucegary.net/HAO/
Resume: http://brucegary.net/resume.html

WebMaster: Bruce L. Gary. This site opened: 2013.02.16. Last Update: 2013.02.21, 16 UT






