Deriving Effective Wavelength from
a Transformation Coefficient
When measurements
are made of calibrated stars (e.g., Landolt stars) using a filter with an
effective wavelength that differs from that for the standard
filter passband, a star color correction term will be required to obtain
the correct magnitudes. For example, consider using a g'-band filter to derive
B-band magnitudes. For my telescope system I have derived the following equation:
B = 19.886 - 2.5 × LOG10 (Flux / exposure)
- 0.19 × AirMass + 0.935 × StarColor
where StarColor = 0.57 × (B-V) -0.39.
This equation works surprisingly well, as
it exhibits a RMS scatter of 0.036 magnitude. Here's a set of "star color
sensitivty dependencies" derived from the use of SDSS filters for deriving
Johnson-Cousins magnitudes;
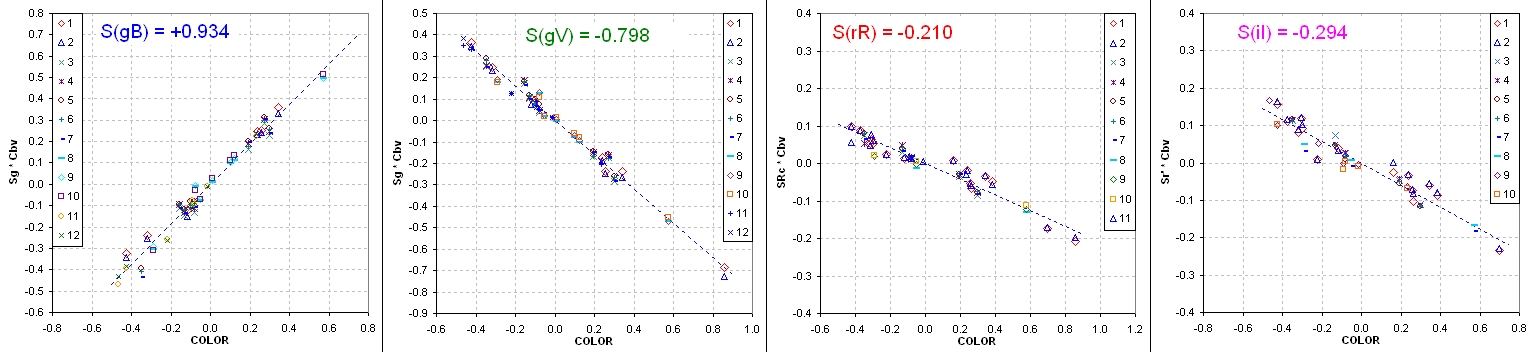
Figure 1. Star color sensitivities for use of SDSS filters in deriving
Johnson-Cousins magnitudes. Observations of 2009.12.24.
Here's a reminder of the differences between (Astrodon filter) SDSS bandpasses
are from the Johnson-Cousins bandpasses:
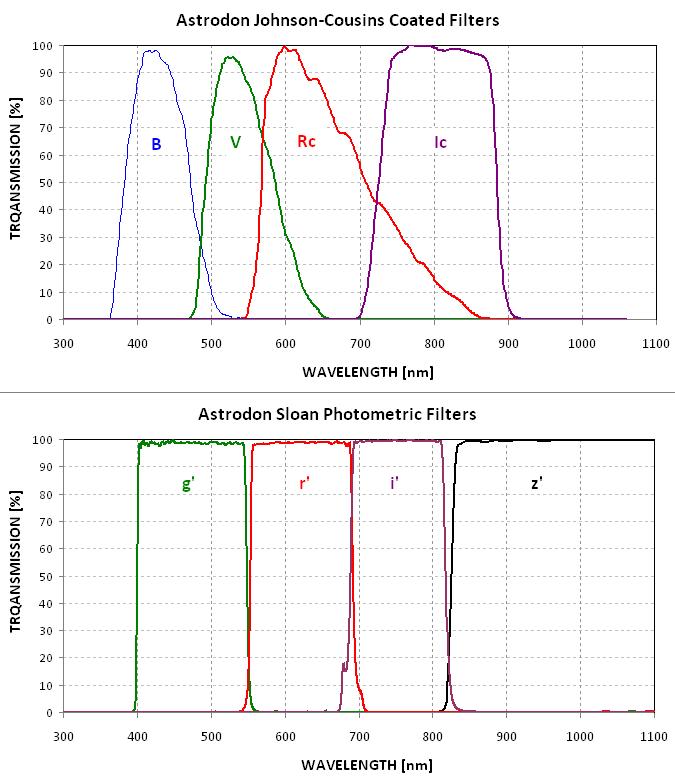
Figure 2. Bandpasses of Johnson-Cousins and SDSS filters.
Notice that the g'-band bandpass is between B- and V-band. We can therefore
expect that red stars will be brighter than expected when using a g'-band
filter for the purpose of inferring B-band magnitudes. In other words, a
+ magnitude correction should be needed for red stars. Indeed, this is what
is foundin Fig.1.
If we had used a B-band filter to infer B-band magnitudes then the star color
sensitivity slope would be much closer to zero. The slope therefore provides
a way for inferring bandpass effective wavelength.
The approximate effective wavelength for g'-band is 485 nm, and for B-band
it's 446 nm (assuming a typical star color). Therefore, to derive an effective
wavelength of 485 nm for g'-band from the B-band effective wavelength of
446 nm plus the star color sensitivity of +0.934 mag/mag, consider the following:
WLeff (g') - WLeff(B) = constant × StarColorSensitivity
(B vs g')
Solving for the constant:
constant = [WLeff (g') - WLeff (B)] / StarColorSensitivity
(B vs g') = (485 - 446) / 0.934 = + 41.8
Which leads to:
WLeff (g') = 446 nm + 42 × StarColorSensitivity
(B vs g')
To the extent that the difference in filter
effective wavelengths exhibits a linear relationship to star color sensitivity,
the constant + 41.8 should apply to the situation of using any filter that
is "near" B-band for determining that filter's exact effective wavelength.
Generalizing, for the case of filters close to B-band, yields:
WLeff = 446 nm + 42 × StarColorSensitivity
(Eqn. 1)
To illustrate use of this equation, consider the following star color sensitivities
from an all-sky observing session that employed Johnson-Cousins filters:
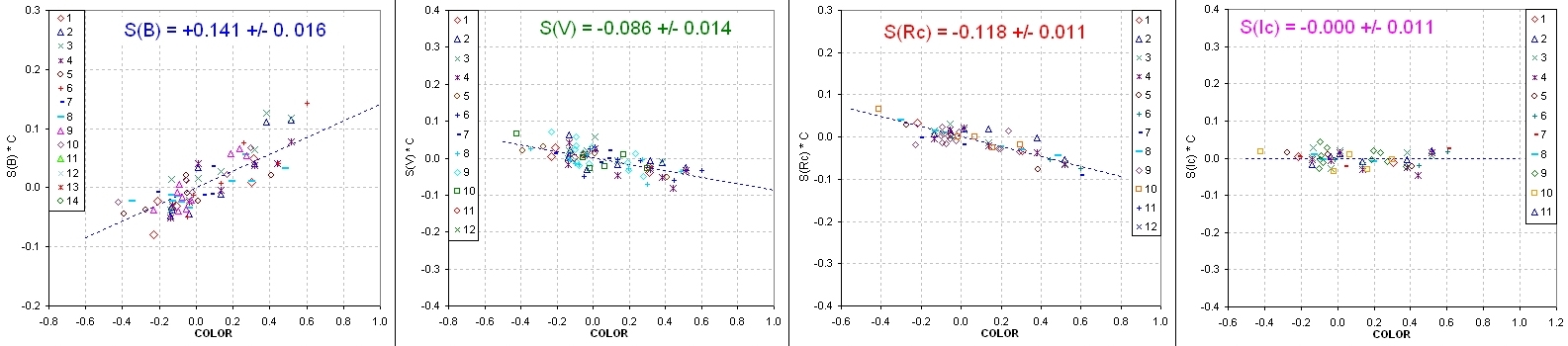
Figure 3. Star color sensitivities for use
of Johnson-Cousins filters. Observations of 2011.10.27. (Magnitude
scale differs from Fig. 1.)
The B-band star color sensitivity is again positive, implying that the effective
wavelength of my B-band filter is greater than the sandard effective wavelength
(of 446 nm). Using Eqn.1, WLeff(B) = 446 nm + 42 × 0.141 = 452 nm.
This corresponds to a shift of 6 nm.
Is there evidence that this is true?
Yes! The effective wavelength for an observation is affected by the telescope's
corrector plate transmission, focal reducer transmission, CCD QE function
and atmospheric transmission. All of these factors affect B-band by reducing
the response at short wavelengths, increasing effective wavelength. For example,
here's what my telescope system and atmosphere are expected to affect B-band
response:
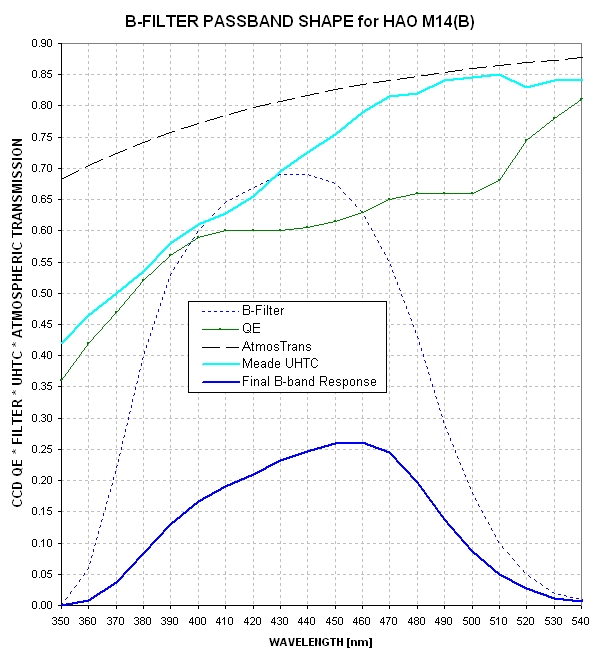
Figure 4. Factors influencing the effective wavelength of my B-band
telescope system response.
And there's a comparison of the original and final filter responses:
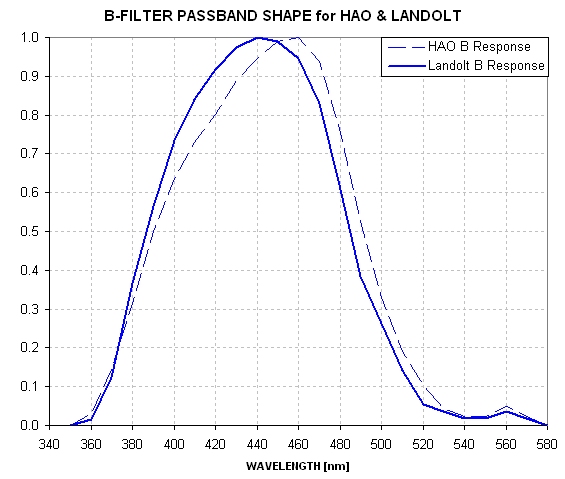
Figure 5. Before and after B-band filter response function.
Visual inspection of this plot suggests that a 15 nm shift in effective
wavelength is possible based on estimates of my telescope optical transmission
function and the CCD's QE function. The purpose for the last two graphs is
to illustrate how easily the effective wavelength of a B-band filter can
be shifted due to effects that are difficult to estimate. It's difficult
to know the filter's exact passband shape, and it is also difficult to know
if the telescope manufacturer's optical transmission function is accurate.
Even the CCD's QE function is somewhat uncertain. Therefore, I don't attribute
any significance to the difference between the predicted 15 nm shift and
the measured 6 nm shift. I trust the 6 nm shift result much more.

WebMaster: B.
Gary. This site opened: 2011.12.25. Last Update: 2011.12.25




