Method#0

J and K to BVRcIc: METHOD #0
0.05 mag SE, 2 Minutes

Bruce L. Gary, Hereford Arizona Observatory (G95)
Last updated 2007.09.02

The 2MASS (2 Micron All Sky Survey) star catalog contains over 1/2 million entries of good quality J, H and K magnitudes. It is ~99% complete for stars having V-mag < 17.5. A typical amateur's FOV will contain dozens of stars with good quality JHK magnitudes. Ever since these magnitude bands were defined and measurements were made with them it has been known that most stars have spectrae that are "well behaved" in the sense that if you know a star's color with any two bands it is possible to predict colors for any other band pair. Of course, the strength of the color/color correlation depend on the star's surface temperature (color), but with the advent of an immense data base of quality JHK magnitudes it is possible to convert JK color to any of the other color pairs with an accuracy that meets most needs. One of the first comprehensive analyses that demonstrated the reliability of these color/color relationships was published by Caldwell et al (1993). Others followed, but my favorite, and the most recently published, is by Warner and Harris (2007). They show that for the color region -0.1 < J-K < +1.0 it is possible to infer B, V, Rc and Ic magnitudes with the following SEs: 0.08, 0.05, 0.04 and 0.035.

Procedure

To calculate a star's magnitude for any of the standard visible bands (BVRcIc) do the following.

   1) Determine the star's J and K magnitudes. This can be done using TheSky/Six (select the UCAC2 information for the star).
        If you don't have TheSky/Six, direct your web browser to http://irsa.ipac.caltech.edu/ and figure out how to get J and K from the IPAC catalog.
   2) Convert from J-mag to BVRcIc using the following equations:

          B = J + 0.198 + 5.215 * (J-K) - 2.7785 * (J-K)² + 1.7495 * (J-K)³           V = J + 0.1496 + 3.5143 * (J-K) - 2.325 * (J-K)² + 1.4688 * (J-K)³           Rc = J + 0.1045 + 2.5105 * (J-K) - 1.7849 * (J-K)² + 1.123 * (J-K)³           Ic = J + 0.0724 + 1.2816 * (J-K) - 0.4866 * (J-K)² + 0.2963 * (J-K)³         You can expect SE = 0.08, 0.05, 0.04 and 0.035provided -0.1 < (J-K)< 1.0.

What could be easier!

You may want more accurate magnitudes, but any alternative for achieving better accuracy will involve much more work. The only exception is if you're dealing with a bright star having Tycho Bt and Vt magnitudes, which can be converted to more accurate B and V magnitudes.

References
Caldwell JAR, Cousins AWJ, Ahlers CC et al (1993) “Statistical Relationships Between the Photometric Colours of Common Types of Stars in the UBVRcIc, JHK and uvby Systems,” South African Astronomical Observatory Circular #15.
Warner, B. D. (2007) “Initial Results from a Dedicated H-G Project," Minor Planet Bulletin, 34-4, pages 113-119.

B and V to RcIc

If you only have B and V magnitudes you can estimate Rc and Ic using the following graphs (with equations included).

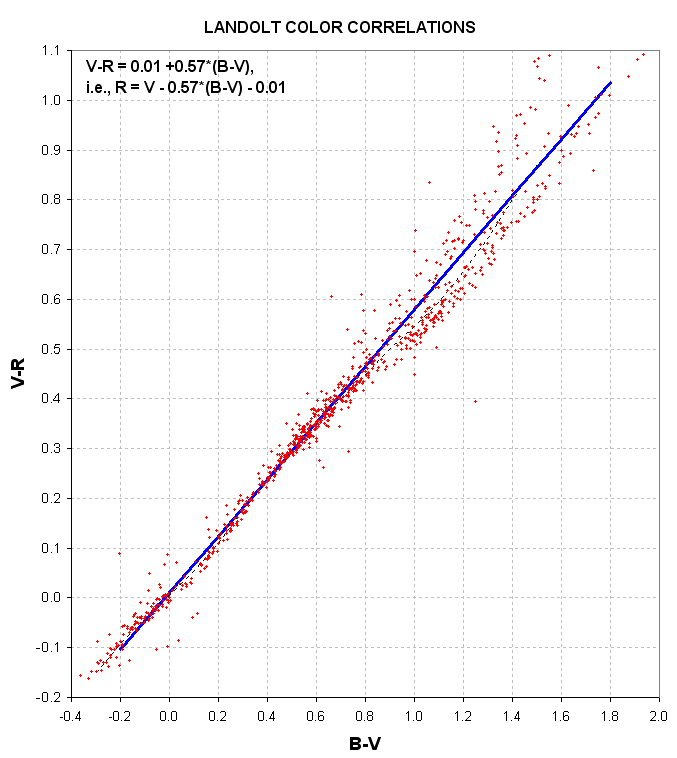
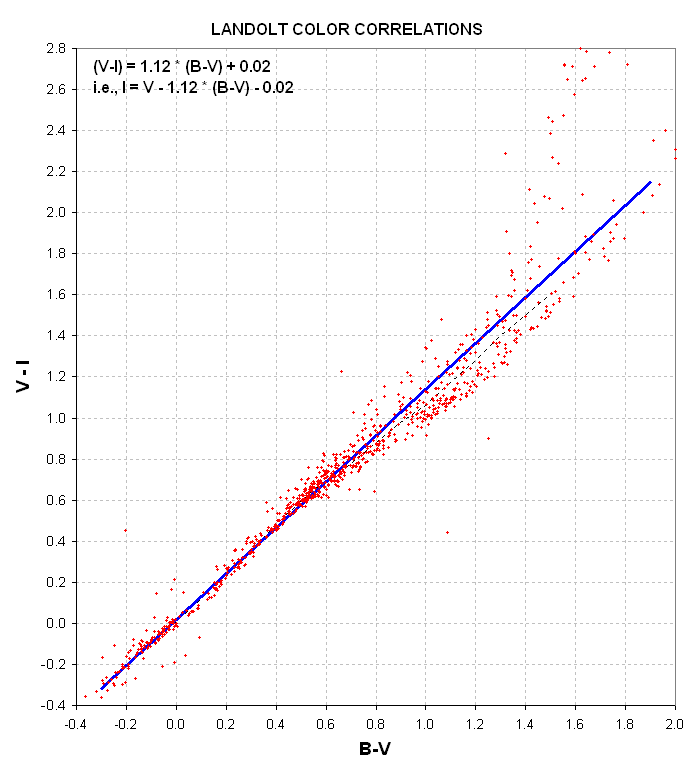
The caution for using tese two plots is that they are valid for main sequence stars, which constitute ~90% of stars.

B and V to RcIc

J and K magnitudes don't exist for bright stars, but those will surely be included in the Tycho list. But Tycho's Bt and Vt have to be adjusted to resemble B and V. Here's how this simple conversion works:

    V = Vt - 0.090 * (Bt - Vt)
    B = V + 0.820 * (Bt - Vt)

or, if you want more accuracy:

    V = Vt + 0.00097 - 0.1334 * (Bt - Vt) + 0.05486 * (Bt - Vt)^2 - 0.01998 * (Bt - Vt)^3 (-0.25 < Bt - Vt < 2.0)
    B - V = (Bt - Vt) - 0.007813 * (Bt - Vt) - 0.1489 * (Bt - Vt)^2 + 0.03384 * (Bt - Vt)^3 (0.5 < Bt - Vt < 2.0)
    B - V = (Bt - Vt) - 0.006 - 0.1069 * (Bt - Vt) + 0.1459 * (Bt - Vt)^2 (-0.25 < Bt - Vt < 0.5 )

For more information about htis and other conversaion equations, click on this link: http://www.aerith.net/astro/color_conversion.html

Return to calling web page: Photometry for Dummies

____________________________________________________________________

This site opened: September 2, 2007. Last Update: March 04, 2008