─────────────────────────────────
CHAPTER 27
─────────────────────────────────
THE
FALL
OF CIVILIZATIONS:
DATING
THE
DEMISE OF HUMANITY
Introduction
This
chapter relates world population data with science and
technology innovations and arrives at a "per capita rate of
innovation" graph. The "per capita rate of innovation" shows
two peaks, one starting during the Golden era of
Population Versus Time
Table 1 is a compilation from
many sources of the world's population for 26 epochs. The original
literature almost never provides uncertainties, but if scatter
is any guide the uncertainties range from 3% during this
century, to ±3 dB (+100/‑50%) at 8000 BC, and ±5 dB at 100,000
BC.
Table
1
Year Pop’n Year
Pop’n Year Pop’n
[AD]
[millions] [AD]
[millions] [AD] [billions]
‑100,000
0.5 1500 440 1950 2.53
‑50,000
1 1600 470 1960 3.0
‑18,000 3 1650 545 1970 3.6
‑8,000 9 1700 600 1980 4.4
‑7500 10 1750 725 1990 5.3
‑3000 30 1800 907 2000 6.38
‑1000 110 1830 1000 2010 7.3
0 200 1900 1600 2025 8.5
1000 340 1930 2000 2038 8.5
A
11th order polynomial fit to the relationship of "log of
population" versus "log of time" is given in Appendix D. It
has been used to perform integrations from the distant past to
dates of interest. The following figure plots the tabulated
data (symbols) and the 11th‑order fit (trace).
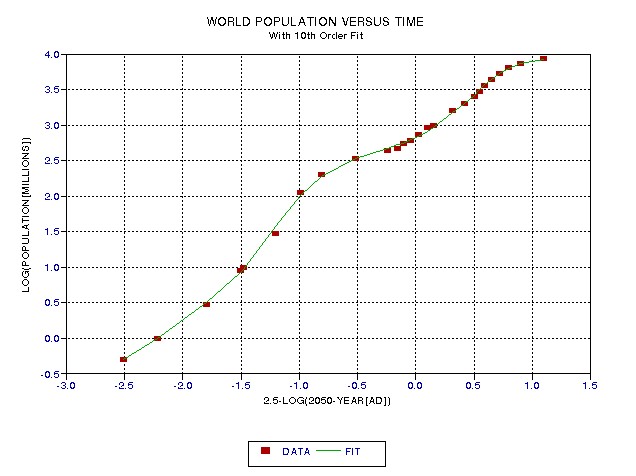
Figure
27.01.
World population versus time, using a special Log scale for
time. The trace
is a 11th order polynomial fit, used to assist in later
calculations.
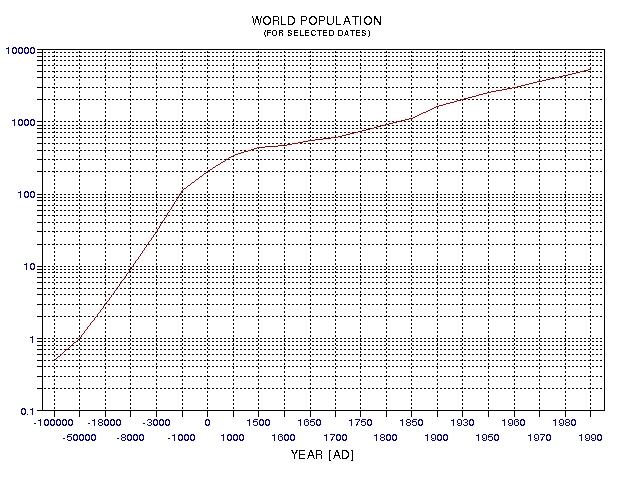
Figure
27.02.
Adopted world population, with arbitrary choice of year for
x‑axis representation.
Birth
and Survival Rates
A
model for birth rates and survival rates versus time (detailed
in Appendix D) was used to create the following plot of
“integrated number of births leading to survival into
adulthood versus time.” Appendix D also includes plots of
“dead to living ratio” versus date, showing that now (2011)
the D/L ratio is ~ 8.
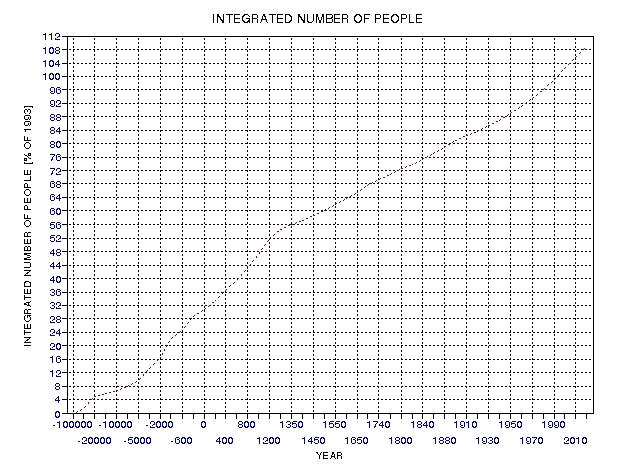
Figure
27.03.
Integrated number of human adults born before x‑axis years.
Innovation
Data
Asimov's
Chronology of Science and Discovery(1980s,
1994) has been analyzed to determine how many innovations
belong to each of the 2%‑intervals of adult human births.
Asimov's list has 1478 entries, from 4 million BC to 1991. In
1991 there had been 19.6 billion “births that lived to
adulthood” (which I’ll refer to as “human lives”). It’s
possible to determine a date corresponding to the first 2% of
human lives (63,000 BC), and 4% (30,000 BC), etc (see Appendix
D for details). For the time span 100,000 BC to the present,
there are 1474 items. A histogram was created showing the
number of items for each 2% date interval. For example, for
the 2% date interval 1891 to 1908 AD, there were 120 citations
in Asimov's list. As there are 2% of 19.6 billion adults
during each 2% interval, or 392 million adults, the number of
innovations per billion people can be calculated by dividing
the number of citations by 0.392. The results of this
conversion are described in Appendix D and presented in the
following figure.
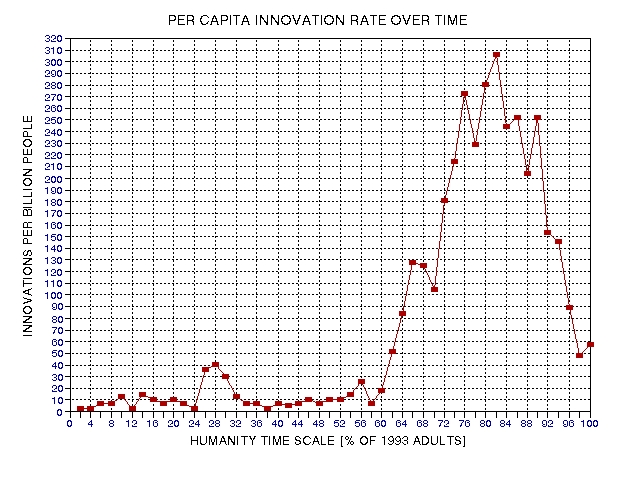
Figure
27.04.
Number of innovations per billion adults for each 2%
interval of the Humanity Timescale.
The
first peak, at 28% (the 2% interval from 26% to 28%),
corresponds to 500 BC to 290 BC. The minimum at 38%
corresponds to the dates 390 AD to 500 AD. The abrupt rise
after 60% corresponds to the mid‑15th Century, which is when
the Renaissance began (1453 AD). The peak at 82%
(corresponding to the 80 to 82% time interval cited above) is
for the period 1891 to 1908 AD. The steady decline since 1908
has progressed to a level corresponding to that of the 16th
Century.
In
Appendix D I argue that a fairer version of this plot is to
make allowance for the varying fraction of a population that
is literate. A model for literacy versus time, by world
regions, is developed in Appendix D. It is used to derive a
plot of literate adults versus date (shown in Appendix D).
This model allows for a calculation of innovation rate per
literate adult versus date (shown in Appendix D).
It
is argued that a better representation of innovation rate per
adult population is to create fictitious population by
weighting it to give greater representation for literate
adults. When this is done the following innovation rate per
“population” is produced. This figure is a plot of the
innovation rate using the weighted average of 4% for
illiterates and 96% for literates. This trace is based on the
concept that the literate person is 24 times as likely (96/4 =
24) to produce an innovation that Asimov would include in his
list compared to the illiterate person. This presentation is
the "fairest" way that I can think of for representing
innovation rate using Asimov's compilation as the measure for
significant innovations.
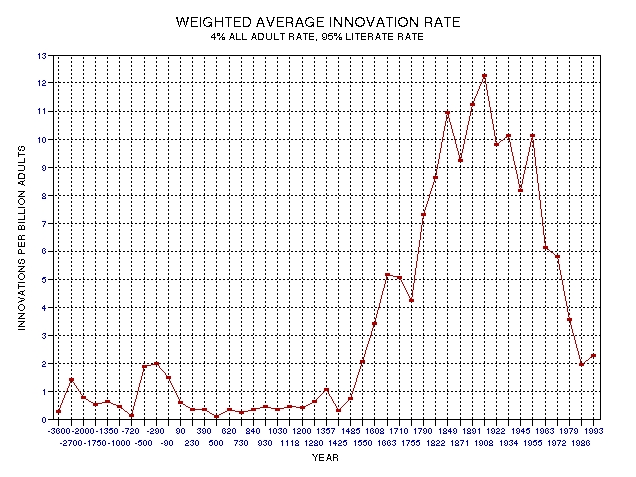
Figure
27.05.
Innovation rate per billion population, weighted average of
rates for literate and all adults assuming (arbitrarily)
that literate adults are 24 times more likely to produce
innovations than illiterate adults.
The
There
are two peaks in Fig. 27.05, as there were in Fig. 27.04. The
classical Greek peak in relation to the 19th Century peak is
13% in Fig. 27.04, and 17% in Fig. 27.05. Normalizing by a
weighted average of literate people and illiterate people's
overall productivity did not significantly change the relative
appearance of the two versions. The Greek peak endures for
about 4 centuries, from 500 BC to 90 BC. The 19th Century peak
occurs between 1550 AD and 1993 AD, approximately, which is
about 4.5 centuries long. Thus, the durations are
approximately the same in terms of normal, calendar time,
being 4 or 5 centuries. I will refer to this most recent peak
as the Renaissance/Enlightenment innovation peak.
There
is another similarity between the Greek and
Renaissance/Enlightenment peaks. They are both accompanied by
an increasing population, and the Greek population rise
reaches a maximum some centuries later. The Greek infusion of
new ideas was exploited by the Romans, who made it possible
for populations to increase until a collapse after 200 AD. The
population maximum occurred 5 centuries after the innovation
peak. Figure 27.06 illustrates this.
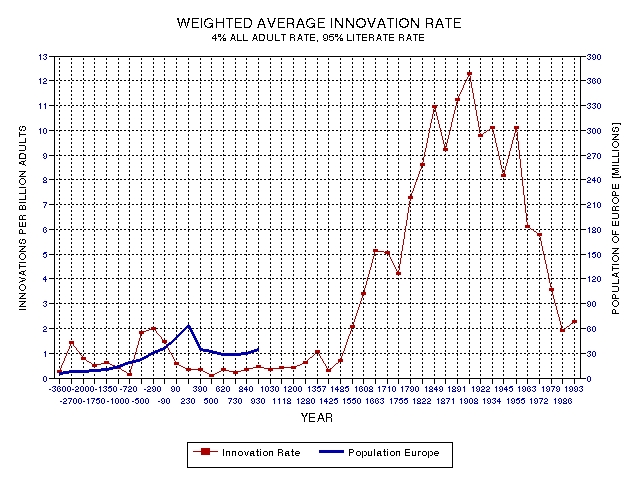
Figure
27.06.European
population in relation to global weighted‑average innovation
rate, showing that the "Greek" innovation peak is followed 5
centuries later by a "Roman" population peak.
Figure
27.07 shows a 1400‑year expanded portion of the previous
figure, centered on the Greek innovation peak. The Roman
population peak follows the Greek innovation peak by 4 to 6
centuries.
Figure
27.08 shows another 1400‑year period, centered on the
Renaissance/ Enlightenment innovation peak. Clearly, this
dynamic cycle is still unfolding, and we who alive today are
naturally interested in its outcome.
It
is inevitable that the still-unfolding
Renaissance/Enlightenment innovation peak will be followed by
a population peak, and I conjecture that its timing will be
similar to the timing of the Greek innovation and Roman
population peaks. We do not know the future, but some
population projections resemble the plot in Fig. 27.09, with a
population peak in ~2200 AD, and a collapse afterwards.
Actually,
this particular future population curve is a special one, for
which I shall present an argument in the next section. Note,
for now, that the population peak occurs only 3 centuries
after the innovation peak, whereas the Roman population peak
followed the Greek innovation peak about 5 centuries. By
analogy, the currently unfolding population explosion in the
undeveloped world owes its existence to the
Renaissance/Enlightenment innovation peak at the end of the
19th Century.
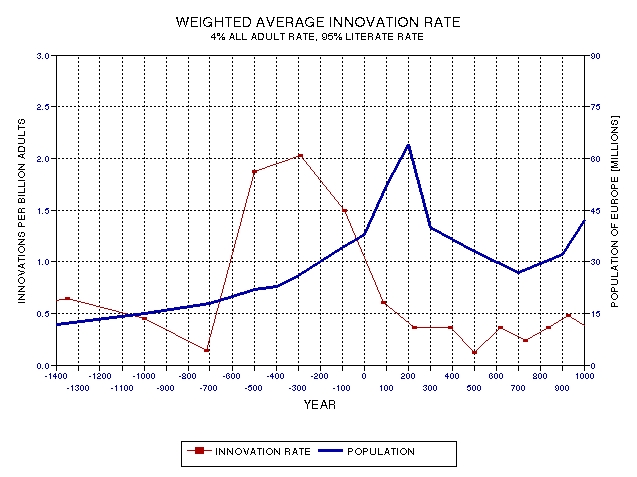
Figure
27.07.
A 1400‑year expanded portion of the previous figure,
centered on the Greek innovation peak.
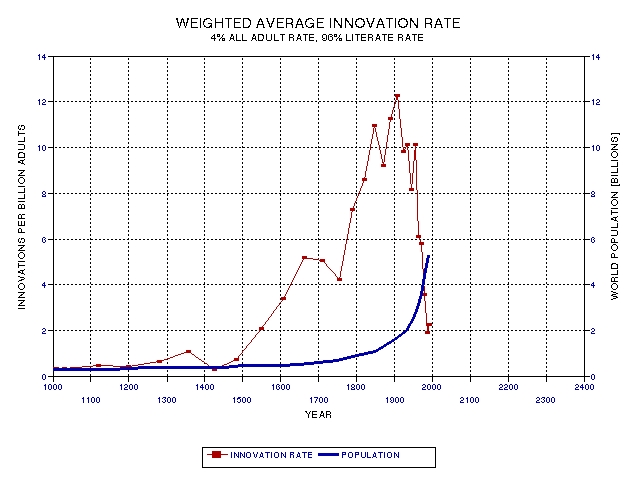
Figure
27.08.Another
1400‑year period, but this time centered on the Renaissance
innovation peak.
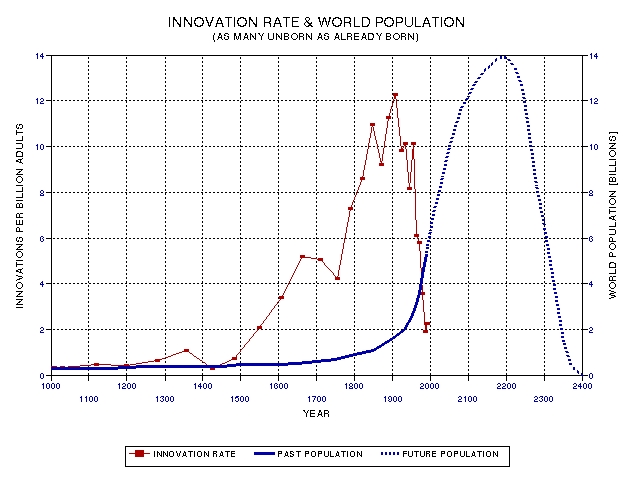
Figure
27.09.The
same Renaissance 1400‑year peak period, but with a future
population trace, showing a population peak after the
innovation peak.
It
is also interesting that for both pairs of
innovation/population peaks, the innovations and population
growth occurred in different parts of the world. The spread of
technology from the site of its origin allows other
populations to grow almost as surely as it allows the
innovating population to grow. This is reminiscent of the old
saying: "When the
table is set, uninvited guests arrive."
Random
Location Principle and Forecasting the Future Population
Crash Date
It
is perhaps important to put the upcoming population crash
scenario to the test of what I shall refer to as the Random
Location Principle. After I performed the analysis presented
here I learned that the subject had been discussed in a late
1980’s publication and was referred to as the “Anthropic
Principle.” A better choice of terminology would be, for
example, The Random Location Principle. It states that "things
chosen at random are located at random locations." This
innocent sounding statement is not trivial. It can have the
most unexpected and profound conclusions, as I will endeavor
to illustrate.
Before
applying the Random Location Principle (RLP) to the population
crash question, let us consider a simpler example that
illustrates the RLP concept. Consider the entire sequence of
Edsel cars built. Each car has an identification number, thus
allowing for the placement of each Edsel in a sequence of all
Edsel cars ever produced. Assume we don't know how many Edsels
were manufactured, and let's try to think of a way to estimate
how many were manufactured by some simple observational means.
Suppose we went to the junk yard and asked to see an Edsel.
Assuming we found one, we could read the identification number
and (somehow) deduce that it was Edsel #4000 (the 4000th Edsel
manufactured). Would this information tell us anything about
the total number manufactured? Yes, sampling theory says that
if we have one sample from the entire sequence, and if it is
chosen at random, then if we double the sequence number we'll
arrive at an estimate of the total number in the sequence. In
other words, doubling 4000 gives 8000, which is a crude
estimate of the length of the entire sequence.
Sampling
theory goes further, and states that we can estimate the
accuracy of our estimate. Namely, we can assume that a sample
chosen at random has a 50% probability of being within the
25th and 75th percentile of the entire sequence. If 4000 were
near the 25th percentile, then the sequence length would be 3
times 4000, or 12,000. If 4000 were near the 75th percentile,
the sequence length would be 4000 * 1.333, or 5300. So, with
just one random sample, the number 4000 in the sequence, we
could infer that there's a 50% probability that the entire
sequence length is between 5300 and 12,000. Stated another
way, there's a 25% probability that the entire sequence length
is less than 5300, and another 25% probability that it is
greater than 12,000.
Now
we’re ready to apply this principle to the human sequence.
Assume every human birth is assigned a sequence number. Let's
delete people who fail to reach adulthood, so our new sequence
is for all people born who eventually become adults. The next
step is going to be difficult for most readers, but I want to
try it. Imagine that the future exists in some sense. It's
like watching a billiards game and having someone exclaim that
while the balls are moving the future motion of the balls is
determined. Thus, after the balls are set in motion the
unfolding of future movements and impacts is determined. So
imagine, if you can, that there is a real sequence of unborn
people who will be added to those already born, and that this
sequence is somehow inherent in the present conditions. If it
helps, think of time as a fourth dimension, and the entirety
of the future is just as real as the entirety of the past, and
the NOW of our experience is just a 3‑dimensional plane moving
smoothly through the time dimension. If you can accept this
concept, then the rest is easy.
Each
person is just one in a long sequence of people comprising the
entirety of Humanity. Few people can expect to find themselves
at a privileged location in this sequence; rather, a person is
justified in assuming that they are located at a "typical"
location in the sequence. For example, there's a 50% chance
that you and I are located between the 25th and 75th
percentile along this sequence of all humans. If we are near
the 25th percentile, given that 19.6 billion adults were born
before us, we could say that another 59 billion adults remain
to be born (i.e., 3 x 19.6 = 58.8). Or, if we happen to be
near the 75th percentile, we could say that another 6.5
billion people remain to be born (i.e., 19.6 / 3 = 6.5). In
other words, there's a 50% chance that the number of humans
remaining to be born is between 6.5 billion and 59 billion. To
convert this to calendar dates, we need to experiment with
future population curves to find those which end with the
required hypothesized number of future adult births.
Consider
the future population trace in Fig. 27.10 that collapses to
zero in 2400 AD. Integrating it to 2400 AD yields 35 billion
new adults. If this is humanity's destiny, then those born in
1993 would be at the 56% location in the entire Humanity
sequence. Or, those who were born in 1939, as I am, would be
located at the 49% location of the entire Humanity Birth
Sequence. These locations are definitely compatible with the
Random Location Principle, and the population projection that
collapses in 2400 AD is an optimal candidate to consider,
since it places today's adults near the mid‑point location of
the Humanity Birth Sequence.
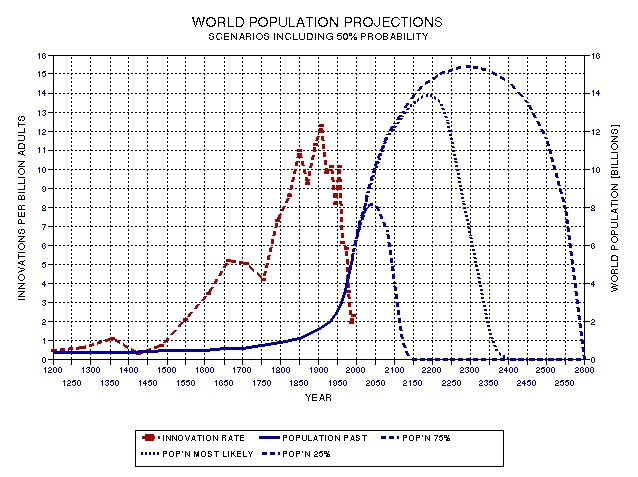
Figure
27.10.Three
future population scenarios, encompassing 50% of what is
forecast by my usage of the Random Location Principle. See
text for disclaimers.
However,
we are searching for a population curve that has an integral
of 6.5 billion new adults, and also a curve with an integral
of 59 billion. Through trial and error I have found two curves
that meet these requirements, and they are also presented in
Fig. 27.10.
The
curve with a population collapse to zero in 2140 corresponds
to the hypothesis that we are currently near the 75% location
in the Humanity Birth Sequence. The population collapsing to
zero at 2400 AD is a most likely scenario, and corresponds to
our being near the 50% location. And the right‑most curve,
with a population collapse to zero at 2600 AD, corresponds to
our current location being near the 25% location. There is a
50% chance that the collapse will occur between the two
extremes. Thus, by appealing to the Random Location Principle,
we have deduced a range of dates for the end of humanity!
The
future population shapes can be rearranged, provided areas are
kept equal. Thus, the real population curve is likely to have
a small "tail." I would argue that after such a colossal
collapse the people surviving and living in the tail would be
genetically and culturally distinct from today's human.
Following the example of Olaf Stapledon, in Last and First
Men (1931), humanity after the collapse will enter a
transition from a First Men phase to a Second Men phase. New
paradigms will define the new man.
Final
Humanity Time Scale
Appendix
D includes a table listing equivalences of "Date" and
"Humanity Time Scale %." The table extends to 200%,
corresponding to the "most likely" population crash date of
2400 AD. The following figure (Fig. 27.11) is a visual
representation of the Humanity Time Scale described by the
equations (modified so that the year 2000 AD corresponds to
the 100% point on the scale), presented in Appendix D.
Caveat
and Comment Concerning Humanity's Collapse
The
population collapse suggested by the "Random Location
Principle" is clearly speculative! Its claim for consideration
hinges on the applicability of the Random Location Principle
to the situation of a sentient being posing the question
"where am I in the immense stretch of humanity?" I suppose the
conventional wisdom, if someone representing it were pressed
to respond to such a question, would say that we are now close
to the very beginning of this immense sequence, and that
humanity may exist forever.
In
addition, that person would say, when our sun expands and
melts the Earth in 5 or 6 billion years, humans will have
migrated to live on a moon of another planet (Titan?) in our
solar system, or maybe we will have traveled to a distant
solar system where an Earth-like planet exists, and humans
will have secured its rightful place as an immortal galactic
species.
Well,
that optimistic belief requires a response to the following:
“If humanity is going to endure for another 6 billion years at
something like its present population level and lifespan, for
example, then isn’t it amazing that we are located at the
0.00006 % place on the long sequence of human existences.” How
likely is it that we are really this close to the beginning of
everything that will comprise the human story? What a
privileged position we would now have if this were true!
HUMANITY
TIMESCALE

Figure
27.11.
Humanity Time Scale. Left scale is for past, right is for
past and future, assuming humanity (as we know it) ceases
after 2400 AD. Equal intervals along the vertical scale
correspond to equal numbers of adults in the entire sequence
of births leading to adults
Miscellaneous
Thoughts on the Meaning of This Result
1)
The Andromeda galaxy is moving toward our Milky Way galaxy at
500,000 kilometer per hour, and the collision date, assuming
it's a direct hit, is approximately 3 billion years from now (Science,
January 7, 2000, p. 64). Speculation over consequences has
just begun, and initial thoughts are that a burst of new star
formation and supernova explosions might bathe the solar
neighborhood with radiation, photon and particle, that could
pose a hazard to all Earthly life, or that too many comets
will be forced out of the Oort cloud and increase the rate of
climate disrupting impacts. I assert that Humanity may not
survive the present millennium, so "not to worry!" about
things 3 billion years from now!
If
only such optimism as worrying about hazards 5 or 6 billion
years from now were warranted! Of course, none of us know if
this will be true. We must be content with speculation. And
mine is merely one conceivable speculation.
2)
It surprised me to discover that for the past century the
innovation rate has been decreasing. At first I thought this
must be due to an under‑representation of innovations from the
20th Century. But the absolute number of innovations continues
to increase during the 20th Century. There's a simpler
explanation. The innovations are coming from slow‑growing
populations of
3)
The careful reader may have wondered "What causes a population
rise following a spurt of innovations?” The rise is easy to
explain, but what causes the decline? This subject is treated
in the many chapters that preceded this one.
4)
It came to my attention March 16, 2000 that many people have
independently stumbled upon the idea for inferring the
imminent demise of humanity, as we know it, using what I
referred to as the "Random Location Principle" ‑ but which
apparently has a generally accepted name, the "Doomsday
Argument," and which is closely associated with a related
topic referred to as the "Anthropic Principle." My original
essay on this subject, “A New Estimate for the End of
Humanity,” appears in Chapter 7 of my 1990 book Essays
From Another Paradigm (self‑published, not for sale).
This essay actually post‑dates similar writings by others by a
few years, but I wasn't aware of any of these writings until
about 1995. A good starting point for learning what others
have written about the subject can be found at: http://www.anthropic‑principle.com/profiles.html
5)
One intriguing way to reconcile the “Doomsday Argument” with a
long human lifespan is to assert that a "long individual
human lifespan" is compatible with the Random Location
Principle and a very long human existence. If biotechnology
affords some lucky individuals the means for achieving
immortality, they may come to dominate world affairs and
eventually extinguish the mortal sub‑species of humans. Then,
the number of humans ever born will have reached a final
maximum number, on the order of 2 or 3 times our present
accumulation, and the Random Location Principle viewpoint will
remain valid even though humanity will extend indefinitely
into the future. For an essay explaining the threat of
nanotechnology, which could include the means for achieving
individual immortality, see the article by Bill Joy at http://www.wired.com/
wired/archive/8.04/joy.html
Appendix
D contains a description of equations presented for those
wishing to reproduce some of the preceding material.
Return to Genetic
Enslavement: A Call for Individual Liberation