ExoplanetObservingforAmateurs

EXOPLANET OBSERVING

FOR AMATEURS

Bruce L. Gary

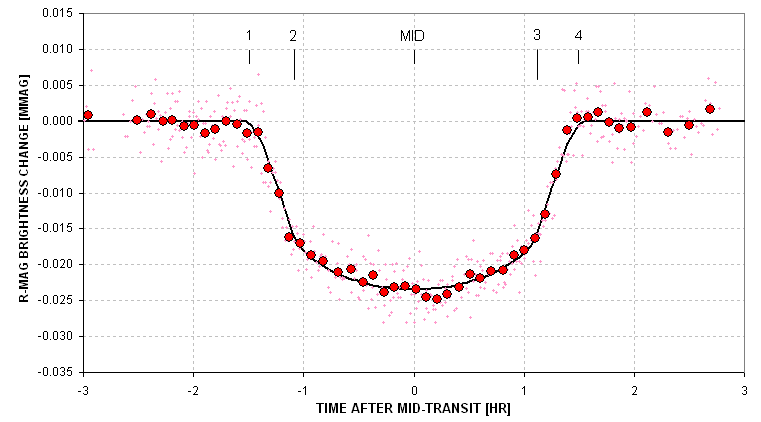
Author’s amateur exoplanet light curve of XO-1 made in 2006 (average of two transits) with a 14-inch telescope and R-band filter at his Hereford Arizona Observatory. Exoplanet XO-1b moves in front of the star during contact 1 to contact 2, is obscuring ~2.2 % of the star’s disk between contacts 2 and 3, and is moving off the star during contacts 3 to 4. The smooth variation between contact 2 and 3 is produced by stellar “limb darkening.”

______________________________________________________________________________________________________________

Reductionist Publications, d/b/a

5320 E. Calle Manzana

Hereford, AZ 85615

Other Books by Bruce L. Gary

ESSAYS FROM ANOTHER PARADIGM, 1992, 1993 (Abridged Edition)

GENETIC ENSLAVEMENT:

A CALL TO ARMS FOR INDIVIDUAL LIBERATION, 2004, 2006, 2008

THE MAKING OF A MISANTHROPE: BOOK 1, AN AUTOBIOGRAPHY, 2005

A MISANTHROPE’S HOLIDAY: VIGNETTES AND STORIES, 2007

EXOPLANET OBSERVING FOR AMATEURS, 2007

QUOTES FOR MISANTHROPES: MOCKING HOMO HYPOCRITUS, 2007

THE MAKING OF A MISANTHROPE: BOOK 2, MIDNIGHT THOUGHTS (2009)

______________________________________________________________________________________________________________

Reductionist Publications, d/b/a

5320 E. Calle Manzana

Hereford, AZ 85615

USA

All rights reserved except for brief passages quoted in a review. No part of this book may be reproduced, stored in a retrieval system, or transmitted in any form and by any means: electronic, mechanical, photocopying, recording or otherwise without express prior permission from the publisher. Requests for usage permission or additional information should be addressed to:

“Bruce L. Gary” <bgary1@cis-broadband.com>

Reductionist Publications, d/b/a

5320 E. Calle Manzana

Hereford, AZ 85615

First edition: 2007 August

Printed by Mira Digital Publishing, St. Louis, MO

ISBN 978-0-9798446-3-8

______________________________________________________________________________________________________________

Dedicated to the memory of

Carl Sagan

A giant among men, who would have loved the excitement of exoplanet discoveries, that would have further inspired him to speculate about

life in the universe.

______________________________________________________________________________________________________________

C O N T E N T S

Preface

Introduction

1 Could I Do That?

2 Observatory Tour

3 Exoplanet Choices

4 Planning the Night

5 Flat Fields

6 Dark Frames

7 Exposure Times

8 Focus Drift

9 Autoguiding

10 Photometry Aperture Size

11 Photometry Pitfalls

12 Image Processing

13 Spreadsheet Processing

14 Star Colors

15 Stochastic SE Budget

16 Anomalies: Timing and LC Shape

17 Optimum Observatory

Appendix A – Flat Field Evaluation

Appendix B – Selecting Target from Candidate List

Appendix C – Air Mass from JD

Appendix D - Planet Size Model

Appendix E – Measuring CCD Linearity

Appendix F – Measuring CCD Gain

Appendix G – Plotting Light Curve Data

Glossary

References

______________________________________________________________________________________________________________

─────────────────────────────────

PREFACE

─────────────────────────────────

The search for planets orbiting other stars is interesting to even my daughters and neighbors. Why the public fascination with this subject? I think it’s related to the desire to find out if we humans are “alone in the universe.” This would explain the heightened interest in exoplanet searchers to find Earth-like planets. NASA and the NSF are keenly aware of this, and they are currently formulating a “vision” for future funding that is aimed at Earth-like exoplanet discoveries.

The author’s favorite telescope, a Meade RCX400 14-inch on an equatorial wedge.

The public’s interest in planets beyond our solar system may also account for Sky and Telescope magazine’s interest in publishing an article about the XO Project, a professional/amateur collaboration that found a transiting exoplanet XO-1 (since then two more discoveries have been announced by this project). The above picture, from the Sky and Telescope article (September, 2006), helps make the point that amateur telescopes are capable of providing follow-up observations of candidates provided by professionals using wide-field survey cameras. The XO Project is a model for future professional/amateur collaborations.

Astronomers, ironically, have traditionally tried to remain aloof from things that excited the general public. I recall JPL cafeteria conversations in the 1970s where I defended Carl Sagan’s right to communicate his enthusiastic love for astronomy to the public. There was a “pecking order” in astronomy at that time, which may still exist to some extent, in which the farther out your field of study the higher your status. Thus, cosmologists garnered the highest regard, and those who studied objects in our solar system were viewed with the least regard. My studies were of the moon, but I didn’t care where I was in this hierarchy. At that time there was only one level lower than mine: those who speculated about other worlds and the possibilities for intelligent life on them.

How things change! We now know that planets are everywhere in the galaxy. Billions upon billions of planets must exist! This is the message from the tally of 248 extra-solar planetary systems (as of mid-2007). Among them are 22 exoplanets that transit in front of their star (15 that are brighter than 13^th magnitude), and the number is growing so fast that by the time this book appears the number could be two or three dozen.

It is important to realize that bright transiting exoplanets are far more valuable than faint or non-transiting ones! The bright transits allow for an accurate measure of the planet’s size, and therefore density; and spectroscopic investigations of atmospheric composition are also possible (successful in two cases). Even studies of the exoplanet’s atmospheric temperature are open for investigation. When 2007 began, only 9 bright transiting exoplanets were known. Six months later there were 14!

Few people realize that part of the explosion of known transiting exoplanets can be attributed to the role played by amateur astronomers. Three of the 15 bright transiting exoplanets were discovered by the XO Project, which includes a team of amateurs. During the past few decades, when professional observatories have become more sophisticated and plentiful, it is ironic that amateurs have kept pace, thanks to improvements in technology that’s within amateur budgets, and we amateurs continue to make useful contributions. The discovery of exoplanet is one of the most fruitful examples!

Not only are amateurs capable of helping in the discovery of exoplanets through collaborations with professionals, but amateurs are well-positioned to contribute to the discovery of Earth-like exoplanets! This is explained in Chapter 16.

How can this be? After all, the professionals have expensive observatories at mountain tops, and they use very sophisticated and sensitive CCD cameras. But with this sophistication comes expensive operation on a per minute basis! With telescope time so expensive, these highly capable facilities can’t be used for lengthy searches. Moreover, big telescopes have such a small field-of-view (FOV) that there usually aren’t any nearby bright stars within an image for use as a “reference.” The optimum size telescope for most ground-based exoplanet discovery has an aperture between 20 and 40 inches, as explained in Chapter 17. Such telescopes are within the reach of many amateurs. So far, most exoplanet discovery contributions by amateurs have been with telescope apertures in the 10 to 14 inches size range. Thousands of these telescopes are in use by amateurs today.

This book is meant for amateurs who want to observe exoplanet transits, and who may eventually want to participate in exoplanet discoveries. There are many ways for amateurs to have fun with exoplanets; some are “educational,” some could contribute to a better understanding of exoplanets, and others are aimed at new discoveries. The various options for exoplanet observing are explained in Chapter 3.

The advanced amateur may eventually be recruited to become a member of a professional/amateur team that endeavors to discover exoplanets. This might be the ultimate goal for some readers of this book. Let’s review how this works. A professional astronomer’s wide-field survey camera, consisting of a regular telephoto camera lens attached to an astronomer’s CDD, monitors a set of star fields for several months before moving on to another set of star fields. When a star appears to fade by a small amount for a short time (e.g., <0.030 magnitude for ~3 hours), and when these fading events occur at regular intervals (~3 days, typically), a larger aperture telescope with good spatial resolution must be used to determine if the brightest star in the survey camera’s image faded a small amount or a nearby fainter star faded by a large amount (e.g., an eclipsing binary). Amateur telescopes are capable of making this distinction since they can quickly determine which star fades at the predicted times and how much it fades. As a bonus the amateur observations can usually characterize the shape of the fading event, whether it is flat-bottomed or V-shaped. If the star that fades has a depth of less than ~30 milli-magnitudes (mmag), and if the shape of the fade is flat-bottomed, there is a good chance that a transiting exoplanet has been identified. Armed with this information the professionals are justified in requesting observing time on a large telescope to measure radial velocity on several dates, and thereby solve for the mass of the secondary. If the mass is small it must be an exoplanet.

As more wide-field survey cameras are deployed by the professionals in a search for transiting candidates there will be a growing need for amateur participation to weed out the troublesome “blended eclipsing binaries.” This will allow the professionals to focus on only the good exoplanet candidates for big telescope spectroscopic radial velocity measurements.

The role amateurs can play in this exploding field is exciting, but this role will require that the amateur learn how to produce high-quality transit light curves. A background in variable star observing would be helpful, but the exoplanet requirements are more stringent, because the variations are so much smaller, that a new set of observing skills will have to be mastered by those making the transition. Image analysis skills will also differ from the variable star experience. This book explains the new and more rigorous observing and image analysis skills needed to be a partner with professionals in exoplanet studies.

The reader is entitled to know who I am, and my credentials for writing such a book. I retired from 34 years employment by Caltech and assigned to work at the Jet Propulsion Laboratory (JPL) for studies in planetary radio astronomy, microwave remote sensing of the terrestrial atmosphere, and airborne sensing of the atmosphere for studies of stratospheric ozone depletion. I have about 55 peer-reviewed publications in various fields, and four patents on aviation safety using microwave remote sensing concepts and an instrument that I developed. I retired in 1998, and a year later resumed a childhood hobby of optical astronomy. I was one of the first amateurs to observe an exoplanet transit (HD209458, in 2002).

I have been a member of the XO Project’s extended team (ET) of amateur observers from its inception in 2004. The XO Project was created by Dr. Peter McCullough, a former amateur, but now a professional astronomer at the Space Telescope Science Institute, STScI. The XO project has announced the discovery of three exoplanets, XO-1b, XO-2b and XO-3b. All members of the XO team are co-authors of the announcement publications in the Astrophysical Journal. I have worked with fellow ET members for 2.5 years, and I am familiar with the issues that amateurs face when changing from variable star observing to exoplanet transit observing. The XO Project is the only professional/amateur collaboration for exoplanet discovery. It is my belief that it will soon become generally recognized that the XO Project model for involving amateurs is a cost-effective and very productive way to achieve results in the discovery and study of exoplanets.

I want to thank Dr. Steve Howell (National Optical Astronomy Observatory, Tucson, AZ) for writing an article for The Planetary Society (Howell, 2002) after the discovery of HD209458b, the first transiting exoplanet to be discovered (Charbonneau, 1999). In this article he explained how accessible exoplanet transit observing is for amateurs, and this led to my first successful observation of an exoplanet transit.

I also want to thank Dr. Peter McCullough for inviting me to join the XO ET in December, 2004. In mid-2006 Chris Burke joined the XO Project, and 5 amateurs were added to the original 4-member ET. Today the ET consists of the following amateurs (names of the original ET are in bold): Ron Bissinger, Mike Fleenor, Cindy Foote, Enrique Garcia, Bruce Gary, Paul Howell, Franco Mallia, Gianluca Masi and Tonny Vanmunster. Thank you all, for this wonderful learning experience and the fun of being part of a high-achieving team.

I am grateful to the Society for Astronomical Sciences for permission to use figures in this book that were presented on my behalf at their 2007 annual meeting and published in the meeting proceedings. Thanks are also due Cindy Foote for allowing me to reproduce her amazing light curves of an exoplanet candidate made with 3 filters on the same night.

Almost all figures are repeated in the “color center insert.”

─────────────────────────────────

INTRODUCTION

─────────────────────────────────

This book is intended for use by amateur astronomers, not professional astronomers. The distinction is not related to the fact that professional astronomers understand everything in this book; it’s related to the fact that the professionals don’t need to know most of what’s in this book.

Professionals don’t need to know how to deal with telescopes with an imperfect polar alignment (because their telescopes are essentially perfectly aligned). They don’t have to deal with telescopes that don’t track perfectly (because their tracking gears are close to perfect). They don’t have to worry about focus changing during an observing session (because their “tubes” are made of low thermal expansion materials). They don’t have to worry about CCDs with significant “dark current” thermal noise (because their CCDs are cooled with liquid nitrogen). Professionals don’t have to worry about scintillation noise (because it’s much smaller with large apertures). Professionals can usually count on sharp images the entire night with insignificant changes in “atmospheric seeing” (because their observatories are at high altitude sites and the telescope apertures are situated well above ground level). Professionals also don’t have to deal with large atmospheric extinction effects (again, because their observatories are at high altitude sites).

If a professional astronomer had to use amateur hardware at an amateur site they would have to learn new ways to overcome the limitations that amateurs deal with every night. There are so many handicaps unique to the amateur observatory that we should not look to the professional astronomer for help on these matters. Therefore, amateurs should look for help from each other for solutions to these problems. In other words, don’t expect a book on amateur observing tips to be written by a professional astronomer; only another amateur can write such a book.

I’ve written this book with experience as both a professional astronomer and a post-retirement amateur. Only the first decade of my professional life was in astronomy, as a radio astronomer. The following three decades were in the atmospheric sciences, consisting of remote sensing using microwave radiometers. Although there are differences between radio astronomy and optical astronomy, and bigger differences between atmospheric remote sensing with microwave radiometers and optical astronomy, they share two very important requirements: 1) the need to optimize observing strategy based on an understanding of hardware strengths and weaknesses, and 2) the need to deal with stochastic noise and systematic errors during data analysis.

This book was written for the amateur who may not have the background and observing experience that I brought to the hobby 8 years ago. How can a reader know if they’re ready for this book? Here’s a short litmus test question: do you know the meaning of “differential photometry”? If so, and if you’ve done it, then you’re ready for this book.

Lessons Learned

One of the benefits of experience is that there will be many mistakes and “lessons learned,” and these can lead to a philosophy for the way of doing things. One of my favorite philosophies is: KNOW THY HARDWARE! It takes time to learn the idiosyncrasies of an observing system, and no observing system works like it might be described in a text book. There usually are a myriad of little things that can ruin the best planned observing session. Only through experience with one particular observing system can these pitfalls be avoided. I therefore encourage the serious observer to plan on a long period of floundering before serious observing is begun. For example, during the floundering phase try different configurations: prime focus, Cassegrain, use of a focal reducer, placement of focal reducer, use of an image stabilizer, etc. During this learning phase try different ways of dealing with finding focus, tracking focus drift, auto-guiding, pointing calibration, etc. Keep a good observing log for checking back to see what worked.

One of my neighbors has a 32-inch telescope in an automated dome, and it’s a really neat facility. But as he knows, I prefer to use my little 14-inch telescope (whenever its aperture is adequate for the job) for the simple reason that I understand most of the idiosyncrasies of my system, whereas I assume there are many idiosyncrasies of his system that I don’t understand.

At a professional observatory the responsibility for “know thy hardware” is distributed among many people. Their staff will include a mechanical engineer, an electrical engineer, a software control programmer, an optician to perform periodic optical alignment, someone to perform pointing calibrations and update coefficients in the control software, a telescope operator, a handy man for maintaining utilities and ground-keeping and a director to oversee the work of all these specialists. Therefore, when an astronomer arrives for an observing session, or when he submits the specifics of an observing request for which he will not be present, all facets of “know thy hardware” have already been satisfied.

In contrast, the amateur observer fills all of the above job responsibilities. He is the observatory “director,” he does mechanical and electrical calibration and maintenance, he’s in charge of programming, pointing calibration, scheduling and he’s the telescope operator – and the amateur is also his own “funding agency.” Thus, when the amateur starts an observing session he has removed his mechanical engineer hat, his programmer’s hat, and all the other hats he wore while preparing the telescope system for observing, and he becomes the telescope operator carrying out the observing request of the astronomer whose hat he wore before the observing session began. The admonition to “know thy hardware” can be met in different ways, as illustrated by the professional astronomer many-man team and the amateur astronomer one-man team.

I once observed with the Palomar 200-inch telescope, and believe me when I say that it’s more fun observing with my backyard 14-inch telescope. At Palomar I handed the telescope operator a list of target coordinates, motion rates and start times, and watched him do the observing. I had to take it on faith that the telescope was operating properly. With my backyard telescope I feel “in control” of all aspects of the observing session; I know exactly how the telescope will perform and I feel comfortable that my observing strategy is a good match to the telescope system’s strengths and weaknesses. Based on this experience I will allege that amateur observing is more fun!

Another of my philosophies is: GOOD DATA ANALYSIS IS JUST AS IMPORTANT AS GETTING GOOD DATA. It is customary in astronomy, as well as many observing fields, to spend far more time processing data than taking it. A single observing session may warrant weeks of analysis. This is especially true when using an expensive observing facility, but the concept also can apply to observations with amateur hardware.

One last Philosophy I’ll mention is: WHEN YOU SEE SOMETHING YOU DON’T UNDERSTAND, WHILE OBSERVING OR DURING DATA ANALYSIS: STOP, DON’T PROCEED UNTIL YOU UNDERSTAND IT. This one is probably difficult to making a convincing case for unless you’ve ignored the advice and wasted time with fundamentally flawed data or analysis procedure. This advice is especially true if you’re writing a computer program to process data, because program bugs are a part of every programming experience. A corollary to this advice might be: Never believe anything you come up with, even if it makes sense, because when there’s a serious flaw in your data or analysis it may show itself as a subtle anomaly that could easily be ignored.

These are some of the themes that will be a recurring admonition throughout this book. Some readers will find that I’m asking them to put too much work into the process. My advice may seem more appropriate for someone with a professional dedication to doing things the right way. If this is your response to what I’ve written, then maybe you’re not ready yet for exoplanet transit observing. Remember, if it’s not fun, you probably won’t do a good job. If you don’t enjoy floundering with a telescope, trying to figure out its idiosyncrasies, then you probably won’t do a good job of learning how to use your telescope properly. This hobby should be fun, and if a particular project seems like work, then consider a different project! Astronomy is one of those hobbies with many ways to have fun, and I dedicate this book to those advanced amateurs who like having fun with exoplanet transit observing.

─────────────────────────────────

Chapter 1

”Could I do that?”

─────────────────────────────────

“Could I do that?” was my reaction 5 years ago to an article claiming that amateurs could observe exoplanet transits (Howell, 2002).

The article stated that transits of HD209458 had even been measured with a 4-inch aperture telescope. Could this be true, or was it hype for selling magazines? The article appeared in The Planetary Society’s The Planetary Report, which was a reputable magazine. I had a Meade 10-inch LX200 telescope and a common CCD camera which I had just begun to use for variable star observing.

“Why not?” I decided, with nothing to lose for trying.

My First Transit Observation in 2002

Before the next transit on the schedule I e-mailed the author of the article, Dr. Steve Howell, and asked if he had any advice. He suggested using a filter, such as V-band (green), and “keep the target near the center of the image.”

On the night of August 11, 2002, I spent about 9 hours taking images of HD209458 with a V-band filter. The next day I processed the images and was pleasantly surprised to see a small “dip” in my plot of brightness versus time that occurred “on schedule” (Fig. 1.01). The depth was also about right, but since my observations were “noisy” they were really a “detection” instead of a measurement. Nevertheless, it felt good to join a club of about a half-dozen amateurs who had detected an exoplanet transit.

By today’s standards my CCD was unimpressive (slow downloads, not a large format) and my telescope was average. The only thing advanced was my use of MaxIm DL (version 3.0) for image processing. Even my spreadsheet was primitive (Quattro Pro 4.0). Today there must be 1000 amateurs with better hardware than I had 5 years ago, based on membership numbers of the AAVSO (American Association for Variable Star Observers).

I recall thinking “If only there was a book on how to observe exoplanet transits.” There couldn’t be such a book, of course, since the first amateur observation of HD209458 had been made less than 2 years earlier by a group in Finland led by Arto Oksanen (http://www.ursa.fi/sirius/HD209458/HD209458_eng.html). Besides, this was the only known transiting exoplanet at that time. Moreover, not many amateurs had a 16-inch telescope like the one used by Oksanen’s team. The idea of amateurs observing an exoplanet transit was a “novelty.” But that was then, and this is now!

I now “know what to do”; to see what a difference that makes look at the next figure.

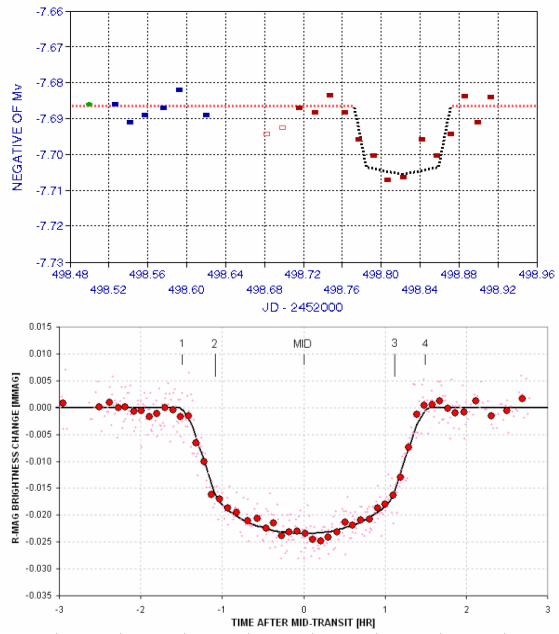
Figure 1.01. Knowing what to do makes a difference. Upper panel: my first light curve of HD209458, made 2002 August 12. Lower panel: a recent light curve of XO-1 made in 2006 (average of March 14 and June 1 transits).

During the past 5 years my capability has improved ~70-fold, and most of this is due to improved technique. Although I now use a 14-inch telescope if I were to use the same 10-inch that I used 5 years ago for my first exoplanet transit I could achieve in one minute what took me 15 minutes to do back then. Some of this improvement is due to use of a slightly improved CCD, and some is from use of a tip/tilt image stabilizer, but most of the improvement is due to improved techniques for observing, image processing and spreadsheet analysis. These are things that can be shared with other amateurs in a book. That’s the book I wanted 5 years ago. You are now holding such a book. It is based on 5 years of floundering and learning. It can save you from lots of time with “trial and error” observing and processing ideas, and give you a 15-fold advantage that I never had for my first exoplanet transit observation.

Minimum Requirements for Exoplanet Transit Observing

You don’t have to live on a mountain top to observe exoplanet transits. My 2002 transit observation was made from my backyard in Santa Barbara, CA, located only 200 feet above sea level. Dark skies are also not even a requirement; my Santa Barbara residence was within the city, and my skies didn’t even resemble “dark” until after midnight. For pretty picture imaging, where dark skies matter more, I disassembled my telescope and put it in my trunk for a drive to the nearby mountains. I now live in Arizona, but my darker skies are only a bonus, not a requirement.

What about “seeing”? Good atmospheric seeing is nice, but again it’s not a requirement. I actually had more moments of good seeing in Santa Barbara than here in Arizona, at a 4660 foot altitude site. In fact, some of the sharpest images of planets come from Florida and Singapore, both sea level sites. Seeing is mostly influenced by winds at ground level, and the height of the telescope above ground. My median seeing in Arizona is ~3.0 “arc for typical exposure times (30 to 60 seconds).

Telescope aperture matters, yes, but an 8-inch aperture is adequate for the brighter transiting exoplanets (10^th magnitude). For most transiting exoplanets a 12-inch aperture is adequate. Since the cost/performance ratio increases dramatically for apertures above 14 inches, there are a lot of 14-inch telescopes in amateur hands. I’ve never owned anything larger, and everything in this book can be done with this size telescope. My present telescope is a 14-inch Meade LX200 GPS. You’ll need a “super wedge” for equatorial mounting.

CCD cameras are so cost-effective these days that almost any astronomical CCD camera now in use should be adequate for exoplanet observing. If you have an old 8-bit CCD, that’s not good enough; you’ll have to buy a 16-bit camera. For a bigger field-of-view, consider spending a little more for a medium-sized chip CCD camera. My CCD is a Santa Barbara Instrument Group (SBIG) ST-8. You’ll need a color filter wheel for the CCD camera, and this is usually standard equipment that comes with the camera.

Although I recommend use of a tip/tilt image stabilizer it’s definitely not a requirement. Few people use such a device for removing small, fast movements of the star field.

Software! Yes, software is a requirement and your choice can be important. I’ve been using MaxIm DL/CCD for 6 years, and it’s an impressive program that does everything. MDL, as I’ll refer to it, controls the telescope, the telescope’s focuser, the CCD, the color filter wheel and the image stabilizer if you have one. It also does an excellent job of image processing, and after it performs a photometry analysis you may use it to create a text file for import to a spreadsheet. Other exoplanet observers use AIP4WIN, and it also does a good job. CCDSoft might do the job, but I find it lacking in user-friendliness and capability.

Spreadsheets are an important program you’ll need to use. Every computer with a Windows operating system comes with Excel, and even though Excel seems constructed to meet the needs of an executive who wants to make a pie chart showing sales, it also is a powerful spreadsheet for science. I’ve migrated all my spreadsheet work to Excel. That’s what I assume you’ll be using in Chapter 13.

Previous Experience

Whenever an amateur astronomer considers doing something new it is natural to ask if previous experience is adequate, especially if there is no local astronomy club with experienced members who can help out with difficult issues. Some people prefer to learn without help, and I’m one of them. The astronomy clubs I’ve belonged to emphasized the eyepiece “Wow!” version of amateur astronomy, so help was never available locally. This will probably be the case for most amateurs considering exoplanet observing. Being self-taught means you spend a lot of time floundering! Well, I like floundering! I think that’s the best way to learn. Anyone reading these pages who also likes floundering should consider setting this book aside, with the intention of referring to it only when floundering fails. For those who don’t like foundering, then read on.

The best kind of amateur astronomy experience that prepares you for producing exoplanet light curves is variable star observing using a CCD. “Pretty pictures” experience will help a little, since it involves dark frame and flat frame calibration. But variable star observing requires familiarity with “photometry,” and that’s where previous experience is most helpful.

One kind of photometry of variable stars consists of taking an image of stars that are known to vary on month or longer time scales, and submitting measurements of their magnitude to an archive, such as the one maintained by the AAVSO. Another kind of variable star observing, which requires more skill, is monitoring variations of a star that changes brightness on time scales of a few minutes. For example, “cataclysmic variables” are binaries in which one member has an accretion disk formed by infalling gas from its companion. The stellar gas does not flow continuously from one star to the other, but episodes of activity may occur once a decade, approximately. An active period for gas exchange may last a week or two, during which time the star is ~100 times brighter than normal. The cataclysmic variable rotates with a period of about 90 minutes, so during a week or more of heightened activity the bright spot on the accretion disk receiving gas from its companion will rotate in and out of view, causing brightness to undergo large “superhump” variations every rotation (90 minutes). The amplitude of these 90-minute variations is of order 0.2 magnitude. Structure is present that requires a temporal resolution of a couple minutes.

Any amateur who has observed cataclysmic variable superhumps will have sufficient experience for making an easy transition to exoplanet observing. Amateurs who have experience with the other kind of observing, measuring the brightness of a few stars a few times a month, for example, will be able to make the transition to exoplanet observing, but it will require learning new skills. Someone who has never performed photometry of any stars may want to consider deferring exoplanet observing until they have some of the more traditional photometry experience.

I’ll make one exception to the above required experience level description. Anyone with work experience making measurements and performing data analysis, regardless of the field, is likely to have already acquired the skills needed for exoplanet monitoring, even if they have never used a telescope. For example, before retiring I spent three decades making measurements and processing data as part of investigations within the atmospheric sciences. I think that experience alone would have been sufficient background for the astronomy hobby that I started 8 years ago. I’ll agree that my amateur astronomy experience when I was in high school (using film!) was helpful. And I’ll also agree that my decade of radio astronomy experience 4 decades ago was also helpful, but the differences between radio astronomy and optical astronomy are considerable. For anyone who has never used a telescope, yet has experience with measurements and data analysis, I am willing to suggest that this is adequate for “jumping in” and starting exoplanet observing without paying your dues to the AAVSO conducting variable star observations! The concepts are straightforward for anyone with a background in the physical sciences.

What are the “entry costs” for someone who doesn’t own a telescope but who has experience with measurements and data analysis in other fields? Here’s an example of what I would recommend as a “starter telescope system” for such a person:

Meade 10-inch telescope

monochrome 16-bit CCD with color filters

equatorial wedge for polar mounting

Maxim DL/CCD

Total cost about $5000

Celestron telescopes are another option, but their large aperture telescopes (>8-inch) are mounted in a way that requires “meridian flips” and these can ruin the light curve from a long observing session.

It has been estimated that tens of thousands of astronomical CCD cameras have been sold during the past two decades, and most of these were sold to amateur astronomers. The number of telescopes bought by amateurs is even higher. Many of these amateur systems are capable of observing exoplanet transits. Amateur astronomy may not be the cheapest hobby, but there are many more expensive ones. With the growing affordability of CCD cameras and telescopes, and a consequent lowering of the $5000 entry level, the number of amateurs who may be tempted by exoplanet observing in the near future may be in the thousands.

Imagine the value of an archive of exoplanet transit observations with contributions from several hundred amateurs. The day may come when every transit of every known transiting exoplanet will be observed (except for those faint OGLE and very faint HST ones). Changes of transit shape and timings are possible, and these can be used to infer the existence of new planets, smaller and more interesting ones. The job is too large for the small number of professional observatories, and the cost of using them for this purpose is prohibitive.

If you are considering a hobby that’s fun and scientifically useful, and if you’re willing to learn new observing skills and spend time processing a night’s images, then welcome to the club of amateur exoplanet observers.

─────────────────────────────────

Chapter 2

Observatory Tour

─────────────────────────────────

Since I will be using real data to illustrate systematic errors I will describe my observing systems. Note the use of the word "systems" in the plural form. Even with one telescope it will matter whether you are configured Cassegrain or prime focus, and whether a dew shield is used, or whether a focal reducer lens is used, and where it's inserted. Every change of configuration will change the relative importance of the various systematic error sources. During the past year I have had three different telescopes, so I am aware of issues related to telescope design differences - such as the problems produced by meridian flips (i.e., Celestrons). All of these telescopes have had 14-inch apertures with catadioptic optics: Celestron CGE-1400, Meade RCX400 and Meade LX200GPS. Most of my illustrations will be with the last one. These are typical telescopes now in use by advanced amateurs for exoplanet transit observations.

I use a sliding roof observatory located in Southern Arizona, at an altitude of 4660 feet. Atmospheric extinction values for B, V, R and I bands are typically 0.25, 0.16, 0.13 and 0.08 magnitude per air mass.

Figure 2.01 “Hereford Arizona Observatory” with a canvas-covered sliding roof. The Minor Planet Center has assigned it a site code of G95.

All control functions are performed by a computer in my house, using 100-foot cables in buried conduit (the control room is shown as Fig.s 2.03 and 2.04). For all Cassegrain configurations I use an SBIG AO-7 tip/tilt image stabilizer. It can usually be run at ~5 Hz. My favorite configuration is Cassegrain (next figure) that has back-end optics consisting of the AO-7, a focal reducer, and a CFW attached to a SBIG ST-8XE CCD. This configuration provides a “plate scale” of 0.67 ”arc per pixel (without binning). Since my “atmospheric seeing” FWHM is usually 2.5 to 3.5 ”arc for typical exposure times (30 to 60 seconds) there are ~ 4 to 5 pixels per FWHM, which is above the 3 pixel per FWHM requirement for precision photometry. The FOV for this configuration is 17 x 11 ’arc.

The Meade LX200GPS comes with a micro-focuser but I removed it in order to have sufficient clearance of the optical backend with the mounting base to be able to observe high declination targets. This configuration also allows me to reach the north celestial pole which is needed for pointing alignment calibration. Without the micro-focuser I need a way to make fine focus adjustments during an observing session (even while continuing to observe a target). This has been achieved by a wireless focuser (sold by Starizona) with the remote unit physically attached to the mirror adjustment focusing knob and the local unit connected to my computer.

Figure 2.02. My favorite configuration: AO-7, focal reducer, CFW/CCD (SBIG ST-8XE). The telescope is a Meade LX200GPS 14-inch aperture, f/10 (without a focal reduce.).

I also have a wireless weather station, with the sensors at the top of a 10-foot pole located near the sliding roof observatory (shown in Fig. 5.01). The pole is wood and the communications are wireless because lightning is common during our summer “monsoon season” (July/August). The weather station is a Davis Vantage Pro 2, supplemented by their Weather Link program for computer downloads from a data logger. This program produces graphical displays of all measured parameters: outside air temperature, dew point, barometric pressure, rain accumulation, and wind maximum and average (for user-specified intervals, which I’ve chosen to be 5 minutes). I find the graphs of wind and temperature to be very useful during an observing session.

Figure 2.03. The author is shown manning the control room at the beginning of an observing session (making flat fields). Equipment is described in the text.

What used to be a “master bedroom” is just the right size for everything needed in an observatory control room. The main computer is connected to the telescope via 100-foot underground cables in buried conduit. This computer has a video card supporting two monitors, one for MaxIm DL and the other for TheSky/Six and other supporting programs (labeled “Monitor #2” in the above figure).

Another computer is dedicated to running the Davis Weather System program that downloads readings from the data logger and displays then as graphs on its own monitor. The Davis Weather System also has a real-time display panel; I find this useful for quick readings of wind speed, wind direction, temperature and dew point temperature when recording outside conditions in the observing log.

A radio controlled UT clock is synchronized with WWVB radio time signals every night. When accurate time-tagging of images is important I visually compare the radio controlled clock with the main computer’s clock, which is synchronized using internet queries by a program (AtomTimePro) at 3 hour intervals.

Above Monitor #1 is a flat bed scanner with a small blanket. This is where the cat sleeps, and occasionally wakes, stretches, and reminds me about observing strategies.

On the desk (behind my chair) is another monitor for display of a wireless video sensor in the observatory. It shows a view of the telescope when a light is turned on by a switch (right side of desk). It also has an audio signal that allows me to hear the telescope drive motors, the sound of the wind as well as barking coyotes. (My two dogs observe with me, on the floor, and they get excited whenever coyote sounds come over the speaker.)

Below the wireless video display monitor is something found in practically every observatory: a “hi fi” for observing music. Since my area is remote, with no FM radio signals, I have a satellite radio (Sirius) receiver with an antenna on the roof and channel selector next to the wireless monitor.

Figure 2.04. Another view of control room.

Sometimes I have to take flat frames while a favorite program is on TV (e.g., “60 Minutes” seems to be the usual one), so I have a second TV on a desk to my left (Fig. 2.04). The remote control for it sits on a headphone switch box (next to the phone). It displays a satellite TV signal that comes from a receiver in the living room.

At the left end of the table in Fig. 2.04 is a secondary computer used to display IR satellite image loops that show when clouds are present. It also offloads computing tasks from the main computer (such as e-mail notices of GRB detections) to minimize the main computer’s competition for resources. This assures that the AO-7 tip/tilt image stabilizer is running as fast as possible. The secondary computer has a LAN connection with the primary computer, which allows downloading images from the main computer for off-line image analysis without interfering with the main computer’s resources.

On top of the main computer (below table, to left) is an AB switch for sending the main monitor’s video signal to another monitor in my living room. This allows me to “keep track of tracking” from my living room chair, while reading or watching TV. The remote monitor in the living room is on a swivel that allows me to keep track of it from my outdoor patio chair. Comfort is important when a lot of hours are spent with this all-consuming hobby.

Charts are taped to every useful area. On one printer is a graph for converting J-K to B-V star colors. On the side of the main monitor is a list of currently interesting exoplanet candidates, with current information from other XO Project observers. Charts are readily visible for estimating limiting magnitude, simplified magnitude equation constants, and a quick way to predict maximum transit length from an exoplanet’s star color and period (same as Fig. B.01). Post-its are used to remind me of handy magnitude equations, site coordinates, local to UT time conversion and nominal zenith extinction values.

─────────────────────────────────

Chapter 3

Exoplanet Choices

─────────────────────────────────

Exoplanets can be thought of as belonging to three categories:

1) bright transiting exoplanets, BTEs (15 known, as of July, 2007)

2) faint transiting exoplanets, FTEs (8 known, as of July, 2007)

3) exoplanets not known to undergo transits, NTEs (225 known)

Those in the first category are by far the most important. This is because transits of “bright transiting exoplanets” (BTEs) allow investigations to be made of the exoplanet’s atmospheric composition and temperature. Atmospheric composition is investigated using large, professional telescopes with sensitive spectrographs. Atmospheric temperature is inferred from thermal infrared brightness changes as the exoplanet is occulted by the star. These investigations can only be done with bright (nearby) exoplanets. In addition to permitting atmospheric studies, the BTEs permit a determination to be made of their size. Since the exoplanet’s mass is known from radial velocity measurements (with professional telescopes) the plant’s average density can be derived. The size and average density allow theoreticians to construct models for the planet’s density versus radius, which lead to speculations about the presence of a rocky core. All of these measurements and models can be used to speculate on the formation and evolution of other solar systems. This, in turn, can influence speculation on the question of “life in the universe.” The rate of discovery of BTEs, shown on the next page, is growing exponentially. Therefore, projects for BTEs that are described in this chapter can be done on a fast-growing list of objects.

The “faint transiting exoplanets” (FTEs) can’t be studied for atmospheric composition and temperature, but they do allow for the determination of exoplanet size and density since transit depth can be measured. Most FTEs are near the galactic plane, near the center, and this makes them especially difficult to observe with amateur telescopes. Although hardware capability improves with time, for both amateurs and professionals, I have adopted the somewhat arbitrary definition of V-mag = 13 for the FTE/BTE boundary. At the present time most amateurs are incapable of measuring transit properties when V-mag > 13.

The many “non-transiting exoplanets” (NTEs) should really be described as not being known to exhibit transits. Of the 225 on the list a statistical argument can be made that probably 10 to 15 of them actually are transiting but observations of them are too sparse to have seen the transits. As more amateurs observe NTEs the BTEs among them will hopefully be identified. This is what happened to GJ 436, which languished on the TransitSearch.org web site list for years before it was observed at the right time and found to undergo 6 milli-magnitude deep transits by a team of amateur observers (Gillon et al, 2007). This underscores the potential value of NTEs for the amateur observer.

For those NTEs that are truly NTE, which is probably 95% of them, since we do not know the inclination of the exoplanet’s orbit we have only lower-limit constraints on its mass. Since transits have not been observed the exoplanet’s size is unknown, which means nothing is known about the planet’s density. Atmospheric composition and temperature can’t be determined since transits don’t occur. Some NTEs may eventually be discovered to undergo transit, and will switch categories.

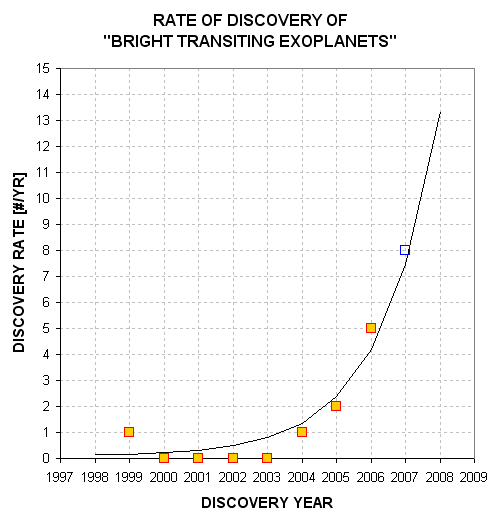
Figure 3.01. Rate of discovery of BTEs. The curve is an exponential fit with a doubling time of ~1.2 years. The open blue square symbol for 2007 is 8 because 4 BTEs were announced during the first 6 months of the year.

Observing Project Types

All categories of exoplanets are worth considering for a night’s observing session. It’s understandable that the beginning observer will want to start by observing a few “easy” transits of BTEs. Once the excitement of this has worn off, however, there may be an interest in other observing projects related to exoplanet transits.

One of my favorite projects is to monitor known BTEs “out-of-transit” (OOT). If no other exoplanets are present in the BTE’s solar system then the observed light curve will be a very uninteresting plot with constant brightness for the entire observing session. However, if another exoplanet exists in the BTE’s solar system its orbit is likely to be in the same plane as the known BTE, and it may produce its own transits on a different schedule from the BTE. Since the known BTE was based on a data base of wide field survey camera observations the transits produced by the BTE will be the easiest to detect. Therefore, an observer searching for a second exoplanet in a BTE solar system should be prepared for a more difficult to detect transit. The second exoplanet’s transit depth will probably be much shallower, and it could either last longer or be shorter, and it will come at times that differ from the BTE transit.

Before selecting an exoplanet to observe extensively in the OOT mode, check its “impact parameter.” This is the ratio “transit chord’s closeness to star center” divided by star radius. If the impact parameter is close to one then it’s a close to grazing transit; this means that any outer planets in that system would not transit. An impact parameter of zero corresponds to a transit that goes through the star’s center; this means that all other planets in the system are likely to transit. As you may have guessed, BTEs have impact parameter values ~0.4, typically. This means that exoplanets in orbits twice the size of the known exoplaent are likely to produce transits. Given that a planetary system exhibits orbital periods that are proportional to orbital radius raised to the 1.5 power, a second exoplanet in an orbit that is twice the size of a hot Jupiter will have a period of 2.8 times that of the hot Jupiter.

There’s a variant of the OOT observing project type, which could be called “looking for Trojans.” This project is based on the presence of Trojan asteroids in our solar system. Jupiter is accompanied by swarms of asteroids in approximately the same orbit as Jupiter but preceding and following by 60 degrees of orbital position. These locations are gravitationally stable and are called Lagrangian points, L4 and L5. There are about 1100 Trojans and none of them are large (exceeding 370 km). If they were lumped together in one object it would have a diameter ~1% that of Jupiter. In solar systems with a Jupiter-sized planet orbiting close to its star, the so-called “hot Jupiter” that most BTEs resemble, the BTE would have to be accompanied by a much larger Trojan companion to produce observable transits. These larger Trojan companions cannot be ruled-out by present theories for solar system formation and evolution, so they are worth an amateur’s attention as a special project. The search strategy is straight-forward: simply observe at times that are 1/6 of a BTE period before and after the BTE’s scheduled transit. In this chapter I’ll show you how to create your own schedule for Trojan transit times.

Another exoplanet project type could be called “mid-transit timings.” The goal is to detect anomalies in mid-transit times caused by the gravitational influence of another planet in a resonant orbit, as described in more detail in Chapter 16. Although this is something one person could do alone it is more appropriate to combine mid-transit timings by many observers in a search for anomalies. The magnitude of the anomalies can be as much as 2 or 3 minutes and the time scale for sign reversals is on the order of a year. Only BTE objects are suitable for this project.

A somewhat more challenging observing project is to refine “transit depth versus wavelength.” Again, this can only be done with BTEs. As the name implies, it consists of observing a BTE at known transit times with different filters for each event. If you have a large aperture (20 inches or larger) you could alternate between two filters throughout an event. The goal is to further refine the solution for the planet’s path across the star and simultaneously refine the star’s limb darkening function. As explained later, an exoplanet whose path passes through star center will have a deeper depth at shorter wavelengths whereas if the path is a chord that crosses farther than about 73% of the way to the edge at closest approach the opposite depth versus color relationship will be found. Constraining the path’s geometry and star limb darkening will lead to an improved estimate for planet size and this is useful for theoreticians studying planetary system formation and evolution.

Every amateur should consider observing nominally NTE exoplanets at times they’re predicted to have possible transits in order to determine whether or not they really are an NTE instead of a BTE that is “waiting” to be discovered. As stated above, GJ 436 is one example of an exoplanet that was nominally identified as an NTE which in fact was discovered to exhibit transits by an amateur group that changed it to a BTE. The nominally NTE list can be found at TransitSearch.org, which is maintained by Greg Laughlin. Times favorable for transits, if they occur, are given on this web site, as well as likely transit depth.

Finally, some exoplanet observers who exhibit advanced observing skills will be invited to join a group of amateurs supporting professionals conducting wide field camera surveys that are designed to find exoplanet transits. So far only the XO Project makes use of amateurs this way, in a systematic way, but other wide field survey groups may recruit a similar team of advanced amateurs for follow-up observations. The main task of these observers is to observe a star field on a list of interesting candidates, at specific times, to identify which star is varying at the times when the survey cameras detect small fades from a group of stars in the camera’s low-resolution photometry aperture. If a star is found that varies less than ~30 mmag it may be an exoplanet, and additional observations would then be required. If the amateur light curves are compatible with the exoplanet hypothesis a professional telescope will be used to measure radial velocity on a few dates for the purpose of measuring the mass of the object orbiting in front of the bright star. A low mass for the secondary almost assures that it is an exoplanet, although careful additional observations and model fitting will be done by the professionals to confirm this. If you’re on the team of amateur observers contributing to follow-up observations that lead to an exoplanet discovery, you will be smiling for days with a secret that can’t be shared until the official announcement is made. Appendix B is included for amateurs on a team charged with wide field camera follow-up observations.

Whenever the night sky promises to be clear and calm the amateur observer will have many observing choices. I suspect that amateur exoplanet observers will eventually form specialty groups, with some specializing in each of the following possible areas:

OOT searches for new exoplanets

Trojan transit searches

BTE timing anomalies produced by another exoplanet in resonant orbit

Transit depth versus filter band

Search for transits by nominal NTEs

Wide field camera candidate follow-up

Calculating Ephemerides for BTEs

Many of the exoplanet observing projects listed above involve the BTEs. This section describes how to calculate when their transits occur.

The following list of known transiting exoplanet systems (brighter than 13^th magnitude) is complete as of mid-2007. It is presented as an example of the kind of list that each transit observer will want to maintain, until such time as it is maintained by an organization dedicated to serving the amateur exoplanet observer (cf. Chapter 17’s description of my idea for an Exoplanet Transit Archive). At the present time http://exoplanet.eu/catalog-transit.php is an excellent web site listing transiting exoplanets (maintained by Jean Schneider). Since it does not list transit depth, transit length, object coordinates or other information useful for planning an observing session I maintain a spreadsheet of transiting exoplanets brighter than 13^th magnitude (BTE_list.xls). Go to http://brucegary.net/book_EOA/xls.htm for a free download of it. Here’s a screen capture of part of it.

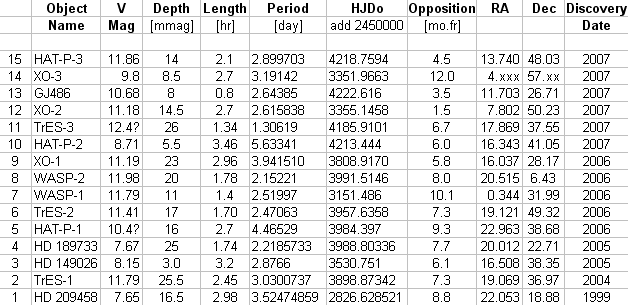
Figure 3.02. List of bright transiting exoplanets (V-mag < 13). The “Opposition” date is the time of year when the object transits at local midnight.

One thing to notice about this table is that all 15 BTEs are in the northern celestial hemisphere. This is due to a selection effect since all wide field search cameras are in the northern hemisphere. If there had always been as many cameras in the southern hemisphere it is fair to expect that we would now have a list of ~30 BTEs. Based on the explosive growth rate shown in Fig. 3.01 the list of BTEs could be in the hundreds in a few years.

Another thing to notice about this table is that 9 of the 15 BTEs are best observed in the summer, June through September. Maybe more BTEs have been discovered in the summer sky because that’s when there are more stars in the night sky (that’s when the Milky Way transits at midnight). It is unfortunate that the northern hemisphere summer is also the time when nights are shortest, and is therefore the least favorable time for observing a complete transit. (Ironically, for my location in Southern Arizona the monsoon season is from July to September, and most of these nights are overcast with a residual of the afternoon’s thunderstorms.)

What’s the table in Fig. 3.02 good for when planning an observing session for an upcoming clear night? You may use this table by first noting which objects are “in season.” The season begins approximately 3 months before “opposition” and ends 3 months afterwards. On those dates the object transits at 6 AM and 6 PM, respectively. An object may be observed “outside” the season, but observing intervals will be limited (the amount will depend on site latitude and object declination).

You’ll want to calculate when transits can be observed. This can be done using a spreadsheet available at: http://brucegary.net/book_EOA/xls.htm. It has input areas for the object’s HJDo, period, transit length, RA and Dec. Another input area is for the observing site’s longitude and latitude. A range of rows with user specified N values (number of periods since HJDo) is used to calculate specific JD values for transits. The JD values are converted to date format for convenience (add 34981.5 and specify your favorite date format). The spreadsheet includes an approximate conversion of HJD to JD (accurate to ~1/2 minute). Columns show UT times for ingress, mid-transit and egress when the object is at an elevation higher than a user-specified value, such as 20 degrees. One page is devoted to each of the 15 known BTEs. The following figure shows part of the display for the XO-1 page.

In this figure cells C2:C6 contain BTE-specific information, such as HJDo, period, length of transit and RA/Dec coordinates. Site coordinates are at F2:F3. The user enters the year at G2 and the UT range that you’re willing to observe in cells G3:G4. Cell H6 is a minimum elevation angle used as a criterion for display of columns E-G. A 4-digit version current JD is entered in cell C7; this is used to suggest to the user a number of periods (elapsed since HJDo) to enter in cell B10. Cells below B10 are integer periods since HJDo that lead to column C’s HJD transit times. Column D converts these values to UT date. Columns H through AB (not shown) are used to calculate elevation angle at the observer’s site (column H). Pages similar in format to this one are present for the other BTEs, so by simply flipping through the spreadsheet pages it is possible to determine whether any of the BTEs are observable on a given night. The user may screen capture each page and print them for later transfer to a monthly observing calendar. As a convenience I mark my calendar a month ahead for all observable BTE transits.

Trojan searches can be scheduled by creating two additional spreadsheets. One of them will require subtracting 1/6 of a BTE’s period from HJDo and the other will have 1/6 period added to HJDo.

A fuller description of the use of this and other spreadsheets that support this book is available at the web site http://brucegary.net/book_EOA/xls.htm.

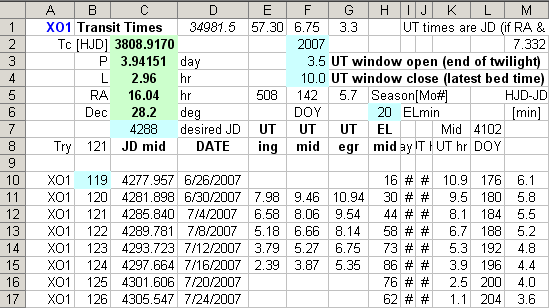
Figure 3.03. Sample Excel spreadsheet showing XO-1b transit events and their “visibility” (from my site). Columns E, F and G show UT times for transits that are above 20 degree elevation and between 3.5 and 10.0 UT. Other details are explained in the text.

SpectraShift

Before leaving the topic of exoplanet projects that are within the reach of amateurs I want to describe an amateur-led project, called SpectraShift, that is designed to detect exoplanets spectroscopically. Radial velocity requirements are demanding since a hot Jupiter orbiting a solar mass star will impart radial velocity excursions of only ±200 m/s if it’s in a 4-day orbit. An amateur group led by Tom Kaye is assembling a system that is expected to achieve 100 m/s resolution using a 44-inch aperture telescope for the brighter BTEs. This group used a 16-inch telescope in 2000 and 2004 to observe Tau Boo and they are credited with being the first amateurs to detect an exoplanet using spectroscopic measurements of radial velocity.

When a wide field survey camera directs an amateur team to candidates for follow-up light curve observations, and when the amateur light curves indicate that the suspect star is indeed fading by small amounts with a flat-bottomed shape, the professionals are often faced with long lead times for obtaining observing time on a large telescope for spectroscopic radial velocity observations that would confirm the secondary as being an exoplanet. When SpectraShift becomes operational, probably in 2008 or 2009, there will be an opportunity for them to collaborate with professional/amateur associations to obtain the required radial velocity observations with short lead times.

Closing Thoughts for the Chapter

There are many ways amateurs can collaborate with professionals in discovering and studying exoplanets. Once basic skills have been “mastered” the simplest project is to choose a BTE and observe it every clear night regardless of when it is expected to undergo transit (OOT observing). This will provide a wealth of data for assessing systematic errors affecting light curve behavior with air mass and hour angle. It may also turn up an unexpected secondary transit produced by a second exoplanet in the far off solar system. This observing strategy could also produce the discovery of a Trojan exoplanet. I recommend OOT observing for anyone who has the required patience and interest in understanding their telescope system.

A slightly more demanding project would be measuring BTE mid-transit times and adding them to a data base of similar observations by others. Eventually a new exoplanet in a resonant orbit will be found this way.

Measurements of transit depth versus filter band can be useful for newly discovered exoplanets since this information will help professionals obtain a better solution for planet size.

Monitoring the NTEs at favorable times will advance the goal of identifying that dozen or so exoplanets that are providing transits that no one has detected yet.

Each person has favored observing styles, and trying out the ones described here is a way to find which one is your favorite. Enjoy!

─────────────────────────────────

Chapter 4

Planning the Night

─────────────────────────────────

This chapter may seem “tedious” to someone new to exoplanet observing. However, keep in mind that the requirements for observing exoplanets, with 0.002 magnitude precision, is significantly more challenging than observing variable stars, with precision requirements that are more relaxed by a factor of 10 or 20. Any amateur who masters exoplanet observing is working at a level somewhere between amateur and professional. Naturally more planning will be involved for such a task.

Probably all amateurs go through a phase of wanting to observe many objects each night. Eventually, however, the emphasis shifts to wanting to do as good a job as possible with just one object for an entire night’s observing. Exoplanets should be thought of this way.

This chapter describes ways to prepare for a night’s observing session. The specifics of what I present are less important than the concepts of what should be thought about ahead of time. Observers who are unafraid of floundering are invited to begin with a total disregard of the suggestions in this chapter since floundering “on one’s own” is a great learning experience. I encourage floundering; that’s how I’ve learned almost everything I know. You might actually conclude that what you learn first-hand agrees with my suggestions.

If you don’t like floundering, then for the rest of this chapter imagine that you’re visiting me in Southern Arizona for an instructive observing session. Together, we’ll plan observations that illustrate decisions that have to be made for a typical exoplanet transit. Let’s assume that it’s 2007 May 5 and you’ve asked me to show you how to observe an exoplanet transit, not yet chosen.

In the afternoon we begin an “observing log.” This is an essential part of any observing session, and starting it is the first step for planning a night’s observations. We begin the log by noting the time for sunset. A table of sunset and sunrise times for any observing site is maintained by the the U. S. Naval Observatory; it can be found at: http://aa.usno.navy.mil/data/docs/RS_OneYear.html. Moonrise and set times are also available at this site. CCD observing can begin about 55 minutes after sunset. Sky flats are to be started at about sunset, the exact time for taking flats depends on the filters that are to be used, the telescope’s f-ratio, binning choice and whether a diffuser is placed over the aperture (treated in the next chapter). Filter and binning choices can’t be made until the target is chosen. That’s what we’ll do next.

Choosing a Target

Since we’re going to spend 6 or 8 hours observing, it is reasonable to spend a few minutes evaluating the merits of various exoplanet candidates. I will assume that you are not privy to one of those secret lists of possible exoplanet candidates maintained by professional astronomers using wide field survey cameras. (If you are such a member, then Appendix C was written for you.)

We want to observe a known transiting exoplanet system, which means we’ll be checking the “bright transiting exoplanet” (BTE) list. If none are transiting tonight then we’ll have to settle for an exoplanet system where transits might be occurring. This “might” category includes exoplanets currently on the NTE list (TransitSearch.org), BTE Trojan searches and undiscovered second exoplanets in resonant orbits that produce shallow transits at unknown times. These categories are described in the previous chapter. Since you’ve asked to observe a transit we’ll be consulting a spreadsheet that I maintain for my site that includes a spreadsheet page for each of the 15 known BTE objects. Each page has a list of transit times with about a month’s worth of transits; as I flip through them we look for transit times for May, 2007. If there aren’t any transits by the BTEs then a “might” category observation will have been considered. We’re fortunate, though, since we note that XO-1 is scheduled to transit tonight. Ingress is at 8:37 PM and egress is at 11:34 PM. At mid-transit XO-1 will be at an elevation of 48 degrees. The sky is clear, the wind is calm, and one of the easiest exoplanets is transiting tonight. Life is good!

Choosing a Filter

XO-1’s brightness is V-mag = 11.2 and the transit depth is ~23 mmag. From past experience using my 14-inch telescope I know that the star’s brightness and the transit’s large depth will make this an easy observation. SNR won’t be a problem, so we aren’t restricted to the use of filters that allow lots of photons to come through, such as clear or a blue-blocking filter (BB-filter). All filter choices are possible.

As an aside, what would our options be if the exoplanet had a shallow depth, or its star was faint? A clear filter would deliver the most light and produce the highest SNR. However, a BB-filter might be better since it excludes blue light (~7%), which means it would reduce the size of one of the most troublesome light curve systematic errors: baseline “curvature” that’s symmetric about transit, caused by reference stars with a different color than the exoplanet star (more details in Chapter 14, “Star Colors”). For small depths this curvature can be troublesome. Observers with 10-inch (or smaller) telescopes should consider using the BB-filter often. Observers with 20-inch (or larger) apertures should rarely have to use the BB-filter. It’s the 12- and 16-inch telescope observers who may have difficult choices for typical exoplanet candidates with depths in the 15 to 25 mmag region.

Since the XO-1 transit is an easy one we are free to review other filter choice considerations, such as “science needs.” If there are no B-band observations for a known exoplanet, then a B-band observation could be valuable. There are occasions when C-filter (clear filter) observing is acceptable. XO-2 is a good example since it has a binary companion 31 ”arc away that has the same color and brightness as XO-2. Because the two stars have the same color there is almost no penalty for observing unfiltered; I’m referring to the “star color extinction effect” that causes baselines to be curved symmetrically about transit. This is explained in Chapter 14, so for now just accept my assertion that the presence of reference stars having the same color as the target star (exoplanet star) is a consideration in choosing a filter. When high air mass observing is required I-band is a good choice (all other things being equal).

The presence of moonlight should influence filter choice. Even though you can’t see it, when there’s moonlight the night sky is blue. A moonlit night sky will be just as blue as a sunlit day sky, and for the same reason (Rayleigh scattering). If the moon will be up during a transit avoid using a B-band filter or a clear filter. I-band observations are affected the least by moonlight. R-band is almost as good, and it passes more light, so if SNR is going to be important consider using an R-band filter on moonlit nights. If SNR is likely to be very important then consider using a BB-band filter, which at least filters out the bright sky B-band photons. The moonless night sky is not blue, but extinction is still greatest at B-band and smallest at I-band, so for dark skies air mass is more important than sky color when choosing a filter. On May 5 at my site the moon rises at 10:35 PM. I recommend using an I-band filter for the XO-1 observations. This is tentative, however, since other considerations are important.

Next, we run TheSky/Six (a “planetarium program” from Software Bisque) to find out the elevation of XO-1 during the night, and specifically during the predicted transit. Acceptable elevations depend on filter; B-band observing will require high elevations (e.g., EL>30 degrees) whereas I-band observing can be done at much lower elevations (e.g., EL>15 degrees). We need to allow for acceptable elevations for the entire transit, from ~1.5 hours before first contact to ~1.5 hours after last contact. Transits of “hot Jupiters” (large exoplanets orbiting close to their star) have transit lengths similar to XO-1, ~3 hours. The best observing situation is for mid-transit to occur at midnight, but this rarely happens. We need to study XO-1’s elevation versus time for the 7 hours centered on mid-transit in order to be sure of our filter choice.

Sunset occurs at 7:03 PM, so quality observing could start at ~7:58 PM (lower quality observations could start at ~7:45 PM). When quality observing can begin XO-1 will be at 20 degrees elevation, and rising. If observing began at 7:58 PM, ~40 minutes of data could be obtained before ingress. That’s pretty short, since we want 1 to 1.5 hours, but it’s just enough for establishing an “out-of-transit” baseline level. After egress there will be lots of data since XO-1 will still be rising and it will be dark. Observations should extend to at least an hour after egress, so let’s plan on observing 2 hours after egress to be safe. Observations of XO-1 will therefore end at ~1:30 AM.

It is worth noting that because observations will start at a low 20 degrees elevation (air mass = ~2.9), B-band observations would be unwise, as would V-band, since both would have high atmospheric extinction values. For similar reasons use of a C-filter would be unwise, since C-band (essentially equivalent to “unfiltered”) includes B-band. Our tentative choice to use I-band is supported by the high air mass situation at the beginning of planned observations. In my experience R-band would be acceptable at ~20 degrees elevation.

For small or moderate aperture telescopes (i.e., 8 - 14 inches) it is wise to observe the target with the same filter the entire night. Large apertures usually provide sufficient SNR to observe with two (or possibly three) filters, in alternation, throughout an observing session.

At this point in the planning process we have chosen a target and filter, but the filter choice is still only tentative. Reference star options have to be considered. This is the subject of the next section.

Deciding on FOV Placement

Even if the observations were to be near zenith there’s a situation that can influence filter choice. It has to do with what stars are near the target star. To be more specific, it has to do with the feasibility of positioning the CCD’s main chip FOV so that a bright star is present in the autoguider chip’s FOV; it also has to do with the desire to have same-color bright reference stars present in the main chip’s FOV. This is where TheSky/Six is very helpful, as the next figure illustrates.

Figure 4.01. XO-1 at center of main chip FOV. Autoguider chip’s FOV is on left.

This figure is a screen capture (inverted) of TheSky/Six with my main chip’s FOV centered on XO-1. There are no bright stars in the autoguider’s FOV, so this positioning is unacceptable. By moving slightly to the right a sufficiently bright star can be used for autoguiding (V-mag = 11.3 according to TheSky). This improved positioning is shown in Fig. 4.02.

The next consideration is “what stars can serve as reference for XO-1?” There’s a bright star in the upper-left corner; but is it the same color as XO-1? Using TheSky, a click of the mouse on XO-1, then a click on the star in the upper left, leads to the answer: XO-1’s J-K = 0.412 and the bright star’s J-K = 0.218. The bright star is bluer than XO-1 by delta J-K = 0.194. The bright star is also 1.38 magnitude brighter than XO-1. Since the brighter star has ~3.6 times the flux of XO-1 we would not be able to use an exposure time that kept XO-1 slightly below saturation. That’s a “down side” to using the bright star for reference. What about the two stars that appear to be about the same brightness as XO-1, and are closer? Figure 4.02 has been annotated with star color for the FOV position that includes the two “same brightness stars” in the main chip’s FOV.

Figure 4.02. Colors (J-K) of XO-1 and possible reference stars.

Note that the two stars similar in brightness to XO-1 are both redder than XO-1; the average difference is 0.12 (using J-K colors). This is half the color difference compared to using the bright blue star in the upper-left, and since longer exposures can be used to place all three stars just below saturation this positioning of the FOVs is a better choice. (An alternative would be to position the main chip’s FOV so that the bright blue star (J-K = 0.22) and the star with J-K = 0.56 are both within the FOV, since the average of their J-K colors differ from XO-1’s J-K by only 0.01 magnitude.)

When there’s a choice between using two reference stars versus using one, it is better to use two. Why? Because of something called “scintillation” that is described in Chapter 15. The average of two stars will have root-2 smaller fluctuations than any single star, regardless of its brightness. Using 4 stars for reference is even better, as their average flux will exhibit ½ the scintillation noise of a single star.

We are fortunate that suitable reference stars are close to XO-1. If only stars with greatly different colors were within the FOV what options would we have for minimizing “star color” extinction effects? V-band and R-band become attractive alternatives to B-band, I-band and BB-band because of their narrower bandpasses. The narrower the bandpass, the smaller “star color extinction” effects are. Since XO-1 is in a “friendly” star field we don’t have to change to R-band or V-band. Our filter choice for the night is now final!

At this stage in formulating a plan for the night we have decided on a target (exoplanet), we’ve decided on an exact placement of the CCD FOV on the star field, and we have settled on I-band. We need to save the exact FOV placement so that it is easily found when observing begins. This is done in TheSky/Six by creating a new object in the “User Defined Data” list and entering RA/Dec coordinates. Planning is almost finished.

Binning

At this point in planning we know an air mass range, so an inference can be made about the sharpest “atmospheric seeing” during the observing session. We consult ClearSkyClock at http://www.cleardarksky.com/ to learn that “average seeing” is expected for the night. In order to know if it is safe to observe with 2x2 binning (instead of 1x1) we need to calculate the sharpest seeing expected during the observing session. At my site FWHM is typically 3.0 ”arc at zenith. Our smallest air mass for the night will be 1.5. Since FWHM is proportional to AirMass^1/3 (cf. Chapter 7) we can plan on FWHM > 3.4 ”arc. A plate scale of 1.7 ”arc or smaller could be used without serious degradation to photometry precision. Since my 1x1 plate scale is 0.67 ”arc we could bin 2x2 and the plate scale of 1.34 ”arc would be acceptable. Based on this, we note in the observing log that we plan on 2x2 binning.

Why observe 2x2 instead of 1x1? There are two reasons. Modern CCD chips perform “on-chip” binning, and they have less “read noise” for 2x2 versus 1x1 binning. The component of “readout” noise is reduced by a factor two for 2x2 binning (since there is only one readout for a 2x2 reading versus 4 readouts for reading the same 4 individual pixels, and noise grows as the square-root of the number of readouts). The second benefit for 2x2 binning is that download times are 4 times faster (e.g., 2 seconds instead of 8 seconds), and this improves the percentage of time spent collecting photons during an observing session (cf. Chapter 7). Knowing whether binning is going to be used affects when flat frame exposures of the twilight sky can begin. If 2x2 binning is chosen for the night’s observing, scheduling of flat frames will have to be made later than shown in Fig. 5.02, as explained in the next chapter.

Finalized Plan

In the observing log we note that the goal for the night is an XO-1 transit and we include the ingress and egress times. We note that an I-band filter will be used, and 2x2 binning will be employed. We don’t know when to start flat fields yet, but we know it will be close to sunset. No configuration changes were made since the previous observing session, and none are planned for the new observing session, so that’s noted.

Since we’ll complete observing at 1:30 AM there’s no need for a nap. We have time before observing begins, so how about joining me for dinner at Delio’s Pizza, a few miles from my place. Besides, every observing session can benefit from pizza snacks, a dark beer and observing music!

There’s only one more thing to do before we can go to dinner, however: scheduling flat field observations. That’s the subject of the next chapter.

─────────────────────────────────

Chapter 5

Flat Fields

─────────────────────────────────

It would be nice if CCDs responded to a uniformly bright source, such as the daylight sky, by producing the same output counts for all pixels. This does not happen for two reasons: pixels differ slightly in their efficiency at converting photons to electrons (and converting electrons to counts during readout), and a uniformly bright sky does not deliver the same flux of photons to all CCD pixels due to such optical effects as vignetting and shadowing by dust particles on optical surfaces close to the CCD (i.e., “dust donuts”).

For amateur telescopes the shape of the vignette function will differ with filter band. The amount of these differences will depend on f-ratio and the presence of a focal reducer (and its placement).

Flat field corrections are supposed to correct for all these things. Alas, in practice flat fields correct for only most of them.

Sometimes I think the art of making quality flat fields could be a hobby, all by itself! It could take so much time that there would be no time left over for using the knowledge gained. There must be a dozen procedures in use for making a master flat, and it’s possible that none of them are as good as the user imagines them to be.

Some observers use “light boxes” placed over the front aperture. Provided the light source is “white” this can produce good flats for all filters. However, it is difficult to attain uniform illumination of the surface facing the telescope aperture – which is where my attempts have always failed.

Another method is to use a white light source to illuminate a white board, which in turn illuminates a second white board that is viewed by the telescope. The use of two white boards reduces specular reflections, which can be troublesome for shiny white boards. The trick with this method is to provide a uniform illumination of the white board viewed by the telescope, and within the confines of a small sliding roof observatory this can be difficult. Wind can also blow over the white boards unless they’re secured. I’ve always obtained good results from this method, but it’s too cumbersome for me to use routinely.

Sometimes master flats are produced by median combining a large number of images of different star fields. For pretty picture work at least a dozen images are needed. For exoplanet observing you would need hundreds of images for median combining in order to reduce residual star effects to the required smoothness needed for mmag precision.

The twilight sky overhead is a convenient way to produce flat fields. For most telescopes these images can be taken when the sky is bright and exposure times are short enough that stars do not appear in any of the images. The telescope can either be stationary or tracking. Master flats produced this way are acceptable for most uses, but for precision exoplanet monitoring the presence of even faint stars in the master flat are unacceptable. A diffuser placed over the aperture can eliminate stars in the flat field images. That’s the method I’ve adopted, which I’ll describe after a detour discussion of stray light.

All flat field procedures can be degraded by “stray light.” For example, an open tube telescope that does not have sufficient baffling in front of the CCD camera may register light from the ground or other locations not within the CCD’s FOV. For another example, I once noticed that my AO-7 image stabilizer was allowing light to leak through the joint formed by the two outer mounting cases. This leak was blocked by simply applying black electrician’s tape around the joint. Light leaks from all “back end” components can be reduced by wrapping a dark cloth around them while exposing flat frames.

Stray light that occurs during an observing session is unimportant for exoplanet monitoring. For example, if there’s a bright star near the exoplanet it may reflect off internal structures and produce rings of light at the same location on all images where the FOV is offset the same amount from the bright star. The nearby moon can produce large brightness gradients in images. Don’t worry about these stray light artifacts. They would ruin pretty picture taking, but photometry is usually unfazed by stray light in the photometry images.

It’s worth noting that flat field corrections wouldn’t be necessary for exoplanet observing if the star field could be positioned at the exact same pixel location for an entire observing session. If that could be accomplished the only errors for neglecting to correct for flat field effects would be limited to star brightness biases, and since these biases would be the same for all images they would not alter the shape or depth of an exoplanet transit light curve.

Keeping the star field fixed with respect to pixels requires not only that the autoguider work perfectly, it also requires that the polar axis be aligned perfectly. Consider observing a source at 60 degrees declination with a polar axis alignment error of only 0.1 degree. During a 6-hour observing session the image would rotate as much as 0.2 degree. The effect is greater for higher declinations. If the autoguider is located 20 ’arc from the center of the main chip, for example, then stars in the middle of the FOV will move 7 ”arc during the observing session, and stars near the corners farthest from the autoguider will move more. If a good quality flat field correction were not made this amount of movement could be ruinous if a target or reference star moved across a “dust donut.” The vignette response function is usually “steep” near the edges, so this is where small inaccuracies in the flat field can produce errors with systematic trends. If a 2 ’arc polar alignment error is present then these effects would probably be too small to correct for, but perfect autoguiding would still be required. Although it’s a worthy goal for amateurs to achieve a perfect polar alignment, and to achieve perfect autoguiding, flat field corrections are a prudent safeguard and must be performed.

I’ll use my telescope system to illustrate how the scheduling of flat frames can be done at about sunset. I point the telescope at zenith well before sunset and place a “double T-shirt” diffuser over the aperture, illustrated in the next figure. The two white T-shirts diffuse sky light, and by using it I never see star trails in my flats. Since the T-shirts let only a fraction of the incident light enter the telescope the sky flat exposures have to begin sooner than if the T-shirt diffuser were not used. Use of the double T-shirt diffuser affords the unexpected bonus of allowing for a more relaxed flat frame observing session. This is due to the fact that the diffuser’s reduction of light entering the telescope requires that flat field exposures begin sooner, when sky brightness changes more slowly.

Figure 5.01. Double T-shirt diffuser is being placed on top of the telescope aperture for obtaining flat fields. (The Davis Weather Station is in the background.)

As mentioned in the previous chapter the time to start exposing flat fields depends on the filter (and binning choice). A photometric B-band filter passes much less light than any of the other filters, so it requires longer exposures for the same sky brightness. A common practice is to keep exposure times within the 1 to 10 second range (explained below). If flat fields are needed for all filters the sequence for exposing flats should start with B-band, and be followed by V-band, I-band, R-band, BB-band and finally clear.

Exposure times shorter than ~1 second can produce slightly unequal actual exposure times at different locations on the CCD. For example, consider a shutter that opens and closes like the old style cameras. As the shutter opened it would begin exposing the CCD center first, and as it closed the center would be the last to have incoming light shut off. This would produce a non-uniform pattern of center-to-edge actual exposure time. The shorter the exposure time the greater the percentage disparity between the center and edge. Rotating shutters are better, but they too have a greater likelihood of producing different actual exposure times at different locations on the CCD for short exposures. CCD camera shutters differ, but exposures longer than ~1 second are generally considered to be unaffected by this problem.

Exposures that are too long are simply inconvenient, and they interfere with making flat field exposures with other filters. Hence, the goal is to schedule the flat field exposures so that they all are within the range of 1 to 10 seconds.

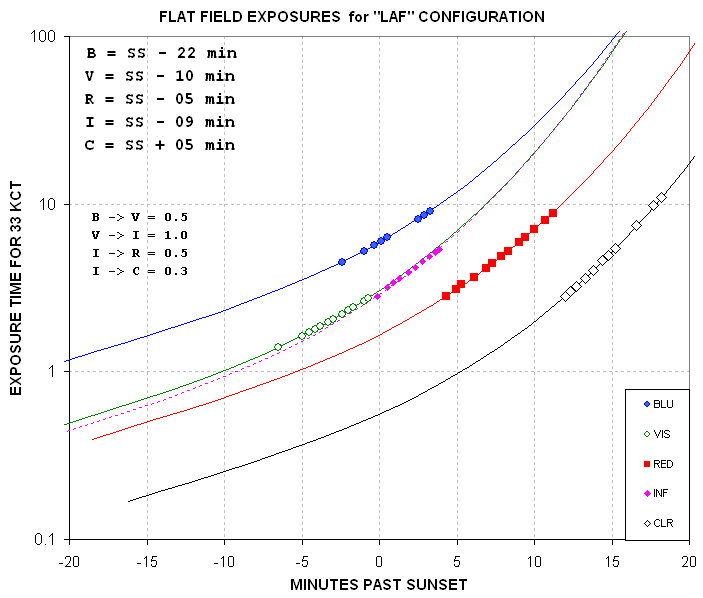
Figure 5.02. Exposure time versus time after sunset for various filters for an f/8 telescope system (binned 1x1) and use of a “double T-shirt” diffuser.

This figure shows that for the B-band filter I can start flat field exposures ~20 minutes before sunset but no later than about 5 minutes afterwards (assuming my binning is 1x1). At 10 minutes before sunset I can start the V-band flat frames. Next are the I-band, R-band and finally the clear filter flat fields. Since the clear filter flats can be made as late as 20 minutes after sunset the entire flat frame series can take 40 minutes, assuming all filters are to be used on that night’s observing session.

Figure 5.02 assumes that no binning will be used (i.e., 1x1 “binning,” or “full-resolution”). If 2x2 binning is planned then flat fields will have to be made later than the times in this graph. Since the CCD’s analog-to-digital converter will be dealing with 4 times the voltage for a specific sky brightness (produced by 4 times as many electrons) we can estimate a time to observe from Fig. 5.02 by choosing the 4-second to 40-second exposure time region; at these times the actual exposures required for the desired counts will be within the range 1 second to 10 seconds.

My sliding roof observatory is usually opened about a half hour before sunset. I immediately start cooling the CCD to something close to 0 C. The flats can be taken at any temperature; according to SBIG they don’t have to be taken at the same temperature as the light frames later in the night. The reason for achieving some amount of cooling is to reduce dark current “thermal” noise.

In making flats it is sometimes stated that dark frame subtractions are optional. This is not true for precision photometry. I strongly recommend the use of dark frame subtraction for all flats. When exposing flats of the sky near zenith after sunset, exposure times have to be increased every few minutes to assure that the maximum count is within a range of values that is slightly below values where non-linearity and other versions of saturation occur. For 16-bit CCDs “A/D converter saturation” occurs at 65,535 counts (“counts” and “ADU” are the same thing). The “conventional wisdom” is to keep the maximum flat field counts within the range 30,000 to 35,000, the latter value being where many observers believe non-linear effects can be expected. Images with maximum counts lower than 30,000 can be used, but the noise component for these images is a greater percentage of the signal component and they may reduce the quality of the combined flat images (the “master flat”). Every time the exposure time is changed a new dark frame has to be taken for use with that flat and those following with the same exposure. This can slow things down, but that’s a fair price to pay for the assurance of minimizing the effects of bad pixels later.

My CCD is linear up to 59,000 counts, and I suspect that the “common wisdom” of avoiding exposures that produce counts above ~35,000 is out of date for modern CCDs. Each observer will want to measure their CCD’s linearity range in order to know how to be guided on setting flat field exposure times, as well as for setting exposure time for stars to be used photometrically. Measuring linearity is described in Appendix E.

When I first started using a CCD I would combine several flat field images and then smooth the resultant image to reduce “noise.” Don’t do this! Every pixel has a slightly different behavior (QE, bias, gain) from its neighbors and this behavior must be preserved in the master flat field image.

I also used to produce a master flat by median combining individual flats (specifying use of the background level for “normalize”). I’ve had a few bad experiences with improper results using the “normalize” setting, which I attribute to the use of flats with too much variation in average level. Because sky brightness is changing fast near sunset it’s difficult to adjust exposure times to produce similar levels for counts in all images. I now favor the averaging of individual flat frames. The only reason to median combine is to remove cosmic ray defects. I rarely see this, but nevertheless it is wise to do a cursory eyeball inspection of the flats before averaging them to make a master flat.

The longer I try to improve flat fields the more I’ve come to believe that perfect flat fields are fundamentally impossible. Even the meaning of a flat field, or the task it is to perform, seems more vague and impossible the more I think about it. I now believe that even the idea of a perfect flat field is theoretically impossible unless it is for an extremely narrow filter. Instead of trying to achieve the perfect flat field it might be better to spend more effort learning to live with imperfect ones.

Consider flats taken near zenith after the sun has set. Since the sky is blue the flats we’re getting this way are meant for use with blue stars. Moreover, since the sky becomes slightly bluer as the sun sinks below the horizon, flats taken shortly after sunset will differ from flats taken late after sunset. In essence, the early and late flats are meant for stars of different blueness. Red stars deserve flats taken with a red sky, but this is not easily achieved. Using a red filter with a blue sky just means the effective wavelength is weighted to the blue side of the filter’s bandpass. In theory we should use a different flat for each star, depending on its color. This, of course, is not practical, even if we knew the color of all the stars in the image. The narrower the filter the less these troublesome effects will be. Unfiltered flats correcting unfiltered images of a star field can therefore be expected to exhibit the worst systematic errors.

An upper limit for the size of these subtle effects can be estimated from all-sky measurements of Landolt star fields using all-sky photometry procedures. When I evaluate telescope constants for all-sky equations for a specific telescope configuration I always have larger residuals for converting unfiltered star fluxes to CV and CR magnitudes than for the observations using a filter (converting B-filter fluxes to B-magnitudes, V-filter fluxes to V-magnitudes, etc). If SNR was the only source of scatter then the opposite should occur. Star color is an independent variable for this analysis so in theory the residuals could be the same for unfiltered and filtered images. I believe the greater scatter for the CV and CR residuals is due to the fact that an unfiltered flat was used with unfiltered images, and the redder or bluer the star the worse the flat field correction. Since the all-sky solution procedure is designed to minimize RMS scatter the final coefficients are a compromise for all star colors in the Landolt set. Typically, I achieve RMS scatter of 0.025 magnitude for the B, V, Rc and Ic data, but only 0.035 magnitude for CV and CR. From this I estimate that the level of systematic effects that can be expected for transit monitoring should be <20 mmag when using a filter and <30 mmag when observing unfiltered. These levels would only be encountered if the target and reference stars were far apart and their pixel locations varied by large amounts during the observing session. When the flat field pattern varies significantly from filter to filter I would expect greater systematic errors from a drift of the star field over the pixel field during an observing session.

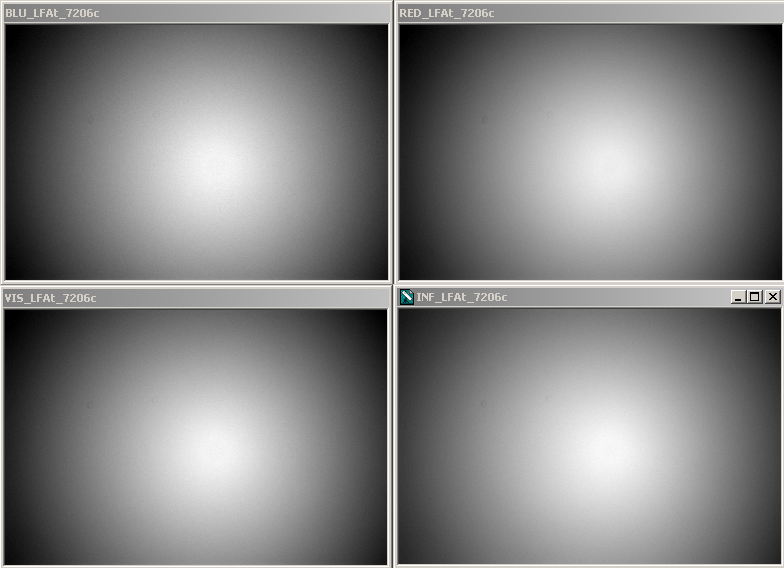
Figure 5.03 Flats for B, V, Rc and Ic filters for a configuration with a focal reducer lens placed far from the CCD chip The edge responses are ~63% of the center.

Figure 5.04 Flats using the same filters but with a configuration with the same focal reducer close to the CCD chip. The response range, smallest response to maximum, are 88, 90, 89 and 89% for the B, V, Rc and Ic filters.

These figures shows how flat fields can change with filter band. Figure 5.03 was made with a focal reducer lens far from the CCD (in front of an AO-7 image stabilizer). Figure 5.04 was made with the focal reducer lens between the AO-7 image stabilizer and the CFW/CCD assembly. What a difference location makes! Also, what a difference filter band makes! For the second set of flats it is easy to imagine that stars of different colors will require flats that are intermediate between the measured blue sky flats, and the reddest stars will have requirements that depart the most from the measured ones.

Appendix A contains methods for evaluating the quality of your master flat field. The procedures described in that appendix are time-consuming, and they are meant for consideration by advanced users.

The entire situation of how to make good quality flat fields and how to use them properly is so confusing to me that I propose the following simple solution. Keep the star field fixed with respect to the pixel field during the entire observing session! If this could be accomplished then the expected small movements of the star field can be counted on to produce only small changes in flat field error for each star, regardless of its color.

The solution I propose to minimize the effects of imperfect flat fields is to achieve an accurate polar axis alignment (< 2 ’arc) and use some form of autoguiding to keep the star field fixed with respect to the main chip’s pixels. With this solution all the fundamental flaws in flat field correcting will be reduced to second-order effects.

─────────────────────────────────

Chapter 7

Exposure Times

─────────────────────────────────

The factors influencing the choice of exposure time can be thought of as belonging to one of two categories: saturation and information rate.

Avoiding Non-Linearity and Saturation

Images are not useful for photometry if any of the stars to be used in the analysis are saturated (i.e., when the maximum count is at the greatest value that can be registered, such as 65,535, called “A/D converter saturation”). Images are also not useful when a star to be used has a maximum count value that exceeds a linearity limit (“linearity saturation”). Not many amateurs measure where their CCD begins to become non-linear, but “conventional wisdom” holds that anything greater than mid-range is unsafe. In other words, whenever the maximum counts, Cmax, exceeds ~35,000 a perfect CCD would produce a slightly higher count.

If you measure your CCD’s linearity limit you may be pleasantly surprised. When I measured mine I discovered that it was linear over a much greater range than represented by “conventional wisdom.” It was linear all the way to 59,000 counts! This measurement can be done using several methods, described in Appendix E. Knowing this has allowed me to use longer exposure times, and longer exposures are desirable for a couple reasons: 1) scintillation and Poisson noise (cf. Chapter 15) are reduced slightly because a greater fraction of an observing session is spent collecting photons (instead of downloading images), 2) read noise is reduced since exposure times can be longer and there are fewer readings per observing session, and 3) a smaller fraction of an observing session is “wasted” with image downloads which means more time is spent collecting photons. I highly recommend that each exoplanet observer measure their CCD’s linearity in order to have the same benefits. For the remainder of this chapter I’ll assume that this measurement has not been made, and you will want to be cautious by using exposure times assuring that all stars to be used have Cmax < 35,000.

You might think that when observations are started it’s OK to just set an exposure that keeps the brightest star from producing a count greater than ~35,000. That’s OK when the star field is already setting, when you can count on images becoming less sharp for the remainder of the observing session. But for rising star fields images are likely to become sharper as they approach transit, and since the same number of total counts from each star will be concentrated on a smaller number of pixels Cmax will increase. Furthermore, atmospheric extinction is lower at transit so each star’s flux, and hence Cmax, should increase as transit is approached.

I recommend taking test exposures for determining exposure time as soon as the target star field has been acquired and focus has been established. Based on previous observing sessions you’ll know whether the sharpness of these images is typical for your site. In making this assessment air mass has to be taken into account. That’s worth an aside.

Image sharpness is described by the “full-width at half-maximum” (FWHM) of the “point spread function” (PSF) of an unsaturated star near the middle of the image. For example, at my site I can expect FWHM ~2.5 ”arc for short exposures (<5 seconds) near zenith and ~3.0 ”arc for exposure times of 30 to 60 seconds. I have determined that at my site short-exposure FWHM varies with air mass (AirMass) in accordance with the following empirical equation:

FWHM [”arc] = 2.5 × AirMass^1/3

This is a useful equation for estimating how sharp an image will be later in an observing session. Suppose the test images at the start of a session show FWHM = 4.0 ”arc when the air mass is 3 (elevation ~ 20 degrees). If “atmospheric seeing” conditions don’t change for the duration of the observing session, and if the region of interest will pass overhead, we should expect that near zenith FWHM ~ 2.8 ”arc.

We can make use of the fact that a star’s Cmax increase as 1/FWHM² for as long as its flux is constant. When FWHM changes from 4.0 to 2.8 ”arc we can expect Cmax to increase by the factor 2.1. Another way of calculating Cmax is to note that Cmax is proportional to 1/AirMass^2/3. In our example, AirMass goes from 3 to 1, so Cmax will increase by a factor (3/1)^2/3 ~ 2.1. This means that we want our test images to show the brightest star’s Cmax = 16,700 (35,000 / 2.1). A more useful version of the previous equation is therefore:

Cmax at AirMass_i / Cmax at AirMass₀ = (AirMass_i / AirMass₀ ) ^-2/3

This equation assumes star flux doesn’t change with air mass. Therefore we must account for changing flux with air mass caused by atmospheric extinction. The biggest effect will be for the B-band filter. Using our example of the test images being made at AirMass = 3, what can we expect for Cmax when AirMass = 1? For my observing site (at 4660 feet above sea level) the B-band zenith extinction is typically 0.25 [magnitude / AirMass]. Changing AirMass from 3 to 1 can therefore be expected to change a star’s measured brightness by 0.50 magnitude. This corresponds to a flux ratio of 1.6 (i.e., 2.512 ^0.5). We therefore must reduce our desired Cmax for test images to 10,400 counts (16,700 / 1.6). At lower altitude observing sites the correction would be greater. See Fig. 14.04 for a graph that can be used to estimate zenith extinction for other observing site altitudes for each filter band.

Imagine the frustration of choosing an exposure time that produces Cmax ~35,000 counts at the beginning of a long observing session, and discovering the next day when the images are being reduced that the brightest stars, and maybe the target star, were saturated in most images! This is a case where a small effort at the beginning of observations can lead to big payoffs for the entire observing session.

Information Rate

When all stars of interest in the FOV are faint the previous considerations may not be important. In this case different criteria should be used to choose exposure time. Starting with a trivial example, if transit length is expected to be 3 hours it would be foolish to take exposures as long as an hour, even though at least one of them would be completely within the transit phase. At the other extreme we don’t want exposures to be significantly shorter than the time required for downloading each image because that would be very inefficient.

Let’s approach this by adopting 60 seconds as a default exposure time, and then ask “what are the merits of either increasing or decreasing exposure time?”

A typical transit will last 3 hours and the ingress and egress portions of this will be ~20 minutes. Referring to the figure on the cover, ingress is from contact 1 to contact 2, and egress is from 3 to 4. For such a transit it is desirable to obtain information about the shape of ingress and egress in order to constrain model fitting (the size of the exoplanet in relation to the star, and also the star center miss distance). Therefore, exposure times should be less than about 4 minutes on account of this consideration. Another reason to have ingress and egress shapes well-established is to be able to assign an accurate mid-transit time. A transit timing archive can be used to establish the presence of “timing anomalies,” and these can be used to infer the existence of another exoplanet in the same star system. I think 4 minutes is the longest exposure time that should be considered for any exoplanet transit observing situation.

What about shorter exposure times? We now must consider a concept called “information rate.” Information rate can be described as inversely proportional to the observing time required to achieve a specified SNR for a specific star using a specified filter. Long image download times reduce information rate. My CCD requires 8 seconds to download (full resolution, or unbinned, or 1x1). If I used an exposure time of 8 seconds half of an observing session would be spent downloading images. Another way of saying this is that such an observing schedule has a 50% duty cycle. Consider the absurd example of exposing for 2 seconds when downloading requires 8 seconds. This corresponds to a duty cycle of 20%, which means 80% of an observing session would be spent simply downloading images. The higher the duty cycle, the greater the information rate. The longest possible exposures will produce the greatest possible information rate.

So why not increase the exposure time from our starting value of 60 seconds, and make it 120 seconds – assuming saturation issues are not a problem at this longer exposure time? To answer this we must consider “risk.” Suppose a satellite, or airplane, passes though the FOV and ruins an exposure? The more exposures you have in an observing session, the smaller is the percentage loss when one image is ruined. There are a myriad of things that can ruin an image. For me, winds vibrate my telescope and when they exceed about 5 mph the stars begin to take on oval shapes. This not only lowers the signal-to-noise ratio (SNR) but it introduces the possibility of systematic errors. Cosmic ray defects are present in most exposures, especially the long ones, and if they appear on top of a star’s image there’s no way for simple aperture photometry to correct for it. If such a cosmic ray defect is within the signal aperture of the target star, or any of the reference stars, the affected image will produce a brightness for the exoplanet that has to be rejected as an outlier. The fewer images that have to be rejected because they appear to be outliers, the better. This is an argument for short exposures.

Consider the information rate for 60-second exposures versus 120-second exposures when download time is 8 seconds: the two duty cycles (proportional to information rate) are 88% and 94%. That’s a gain of only 7% for the longer exposure time, but a doubling of “risk” related to ruined images.

Scintillation noise is a possible consideration when choosing exposure time. Scintillation noise is a fractional fluctuation of all stars in a FOV, uncorrelated with each other, caused by wave front interference effects produced by small-scale temperature inhomogeneities at the tropopause (11 - 16 km at zenith). Scintillation fluctuations of a star’s intensity decrease with exposure time as 1/g^1/2 (where g is exposure time). Thus, 4-minute exposures will exhibit half the scintillation of 1-minute exposures. However, the average of four 1-minute exposures will also exhibit half the scintillation of a single 1-minute exposure. The only improvement in reducing scintillation by using longer exposures comes from the fact that a 4-minute exposure can be obtained more quickly than four 1-minute exposures (due to the difference in number of image downloads). Using the previous example, in which a 4-minute exposure has a 7% advantage in duty cycle compared to 1-minute exposures, we can calculate that a sequence of 4-minute exposures will have a 3.4% lower scintillation per unit of observing time than the sequence consisting of 1-minute exposures (sqrt(1.07) = 1.034).

The same argument can be applied to Poisson noise (described in Chapter 15). The fractional uncertainty of a flux measurement due to Poisson noise is proportional to 1/flux^1/2 and since flux is proportional to exposure time the same 1/g^1/2 relationship exists between Poisson noise and exposure time.

I don’t know of an objective way to assess all these factors, but they will be different for each observatory. It is my subjective opinion that 60-second default exposure time is a good compromise when saturation considerations permit it.

─────────────────────────────────

Chapter 8

Focus Drift

─────────────────────────────────

I once neglected to "lock the mirror" after establishing a good focus, and went to sleep while observing a transit candidate. I'm glad this happened; the focus drifted and caused an effect that was too obvious to ignore, and this led me to investigate causes. The problem showed itself as an apparent "brightening" of the target (relative to several reference stars) near the end of the observing session.

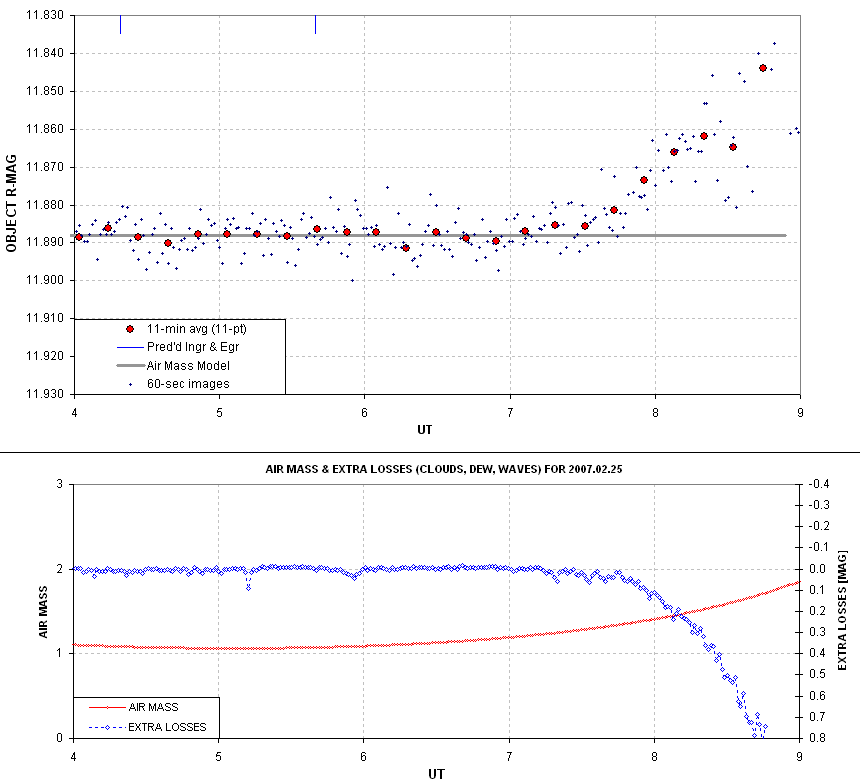
Figure 8.01. Light curve showing effect of focus drift starting at ~7.2 UT. The lower blue trace shows that the “sum of fluxes for all reference stars” decreased starting at the same time.

I recall upon awakening, and looking at the image on the monitor, that the focus was bad and I immediately suspected that this was caused by focus drift, but I didn't know what effect it would have on the light curve (LC). After processing the images and seeing the LC, I knew right away that focus drift had affected it. Here's a plot of FWHM (and “aspect ratio”) for the images used in the above figure.

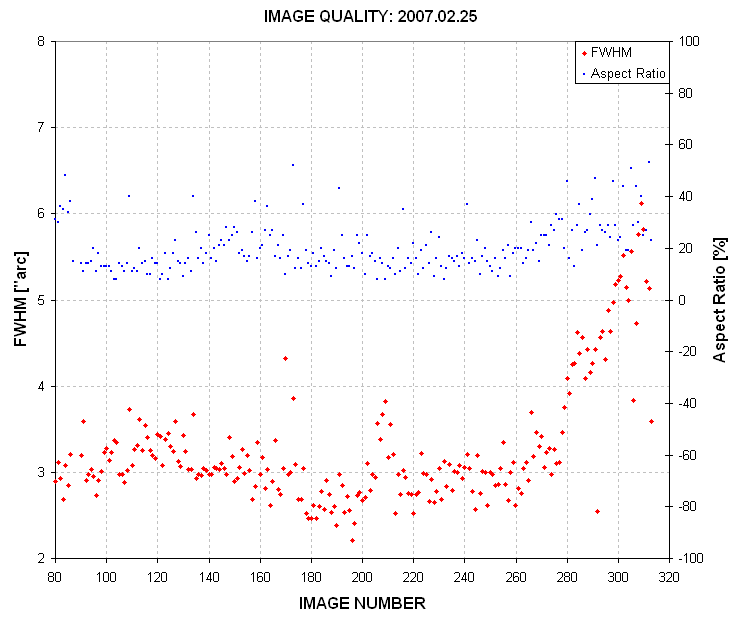
Figure 8.02. Plot of FWHM ["arc] and "aspect ratio %" (ratio of largest PSF dimension to smallest, expressed as a percentage) for the images used to produce the light curve. Image numbers near 260 correspond to 7.0 UT. (Produced using the automatic analysis program CCDInspector, by Paul Kanevsky.)

There's clearly a good correlation between focus degrading and the apparent brightening of the target star (~7.0 UT). But how can an unfocused image affect the ratio of star fluxes? To determine this, consider how MaxIm DL (and probably other programs as well) establish magnitude differences from a set of images. I'll use two images from the above set to illustrate this.

An image in good focus was chosen from ~7.0 UT and another from ~8.5 UT. They were treated as a 2-image set using the MaxIm DL photometry tool. The next figure shows the sharp focus image after a few stars were chosen for differential ensemble photometry.

Figure 8.03. Location of photometry apertures after using this image to select an object (the “target” or exoplanet candidate), check stars and a reference star (upper-left corner, my artificial star). (These notations are slightly misleading, as explained in the text.)

The measured star fluxes are recorded to a CSV-file (comma-separated-variable in ASCII format) which can be imported to a spreadsheet, where the user can select from among the “check stars” to serve as reference. The artificial star is not used for reference; instead it serves to determine “extra losses” that might be produced by clouds, dew on the corrector plate, or image quality degradations due to poor tracking, wind shaking the telescope or poor focus (causing the PSFs to spill outside the photometry aperture). These details are not relevant to this chapter’s message, and they’ll be treated at length in Chapters 12 and 13.

Note that in this image essentially all of each star's flux is contained within the signal aperture. The next figure is a screen capture of the photometry circle locations on the defocused image.

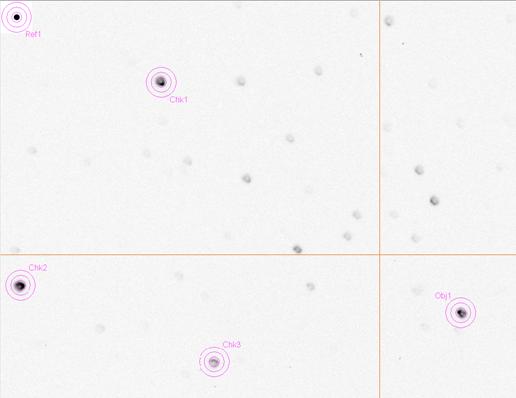
Figure 8.04. Same photometry apertures (at the same x,y locations as in the previous image) for the defocused image.

In this defocused image some stars have PSFs that are spread out in the famous “comet shape” coma pattern, with the comet tails directed away from the optical center (indicated by the cross hair). The length of the coma tail is greater the farther the star is from the center. Thus, stars near the edges have a smaller fraction of their total flux within the aperture than stars near the center. The ratio of fluxes, and hence magnitude differences, will therefore be affected. The object's measured brightness can have either sign, depending on whether the target star (the exoplanet candidate, labeled “Obj1” in the figure) is closer to the center, or farther from it, compared with the reference stars (labeled “Chk” in the figure). For this image we can expect the reference stars to suffer greater losses than the target, leading to an apparent “brightening” of the target. The magnitude of this effect will be greater for smaller photometry apertures. Larger apertures would reduce this effect. However, the best solution is to never have to use poorly focused images.

Referring back to Fig. 8.01, and noting the blue trace labeled "Extra Losses [mag]", an increase in losses is usually produced by cirrus clouds. However, in this case it was produced by a spreading out of the PSF beyond the signal aperture circle as focus degraded.

The lesson of this chapter is “keep all images in good focus” (an exception is treated at the end of this chapter). If that doesn’t work, for whatever reason, then when processing the images use a large photometry aperture to assure that most of the flux is measured for all stars (“most” means ~99%). If you’re not sure that the aperture size was sufficiently large, then if you use an artificial star for setting the differential magnitudes check to see if the magnitude for any of the stars, or the magnitude corresponding to total flux for all the non-target stars, drops when the target appears to change values. Any correlation between target brightness and fading of reference stars should be viewed as a “red flag” for focus drift problems.

Observing Log Entries

I like to record in the observing log FWHM measurements of a chosen star at regular intervals, such as every half hour. This helps in identifying the need for a focus adjustment; it also will show the presence of atmospheric seeing trends. Since my focus setting depends on elevation as well as temperature, I also record these values.

Whenever I record a FWHM in the observing log I also record the magnitude that MaxIm DL displays when the photometry circles are over the star that I’ve chosen for that purpose. It doesn’t matter that the magnitude scale is uncalibrated (i.e., having an offset error) because the only thing I’m monitoring is constancy of the chosen star’s brightness. This is a good way to detect the presence of cirrus clouds. It also can alert for the presence of dew accumulation on the corrector plate. You can’t do anything about cirrus clouds, but dew accumulation will require use of a hair dryer. By choosing a bright (unsaturated) star for this purpose the magnitudes should be constant at a level of <0.01 mag (assuming SNR > 100). Changes from one image to the next that exceed this usually indicate the presence of clouds. Slow changes will of course occur due to changing air mass, but these changes are small and easily identified as air mass related. For example, R-band observing will increase the star’s magnitude by ~0.13 magnitude per air mass, and if the observing log includes elevation notations it is easy to verify that trends are compatible with an atmospheric extinction explanation. I also like to record outside air temperature, dew point, wind max (during the past 5 minutes) and wind direction. Whenever focus is adjusted I note this as well.

Intentional Defocusing

Sometimes an observing session is designed for intentionally defocused imaging. This is done when bright stars are within the FOV and Cmax must be kept below saturation for long exposures. The desire for long exposures can be motivated to reduce the fraction of time lost to image downloading or to reduce scintillation (cf. Chapter 15). There are situations when this can be done safely. One requirement is a good alignment of the telescope optics; otherwise, defocused images won’t have circularly symmetric point-spread-functions. Another requirement is that the telescope tube does not contract as the night air cools, which would require that adjustments be made to maintain the same defocus. Defocused observing should not be attempted when there are stars near the target or reference stars that could be included in the signal photometry aperture. This is more often a problem for objects at low galactic latitudes. Finally, this should only be done at sites where sky background level is not high, since a defocused image will require the use of a larger photometry aperture and large photometry apertures increase the component of sky background noise to the final measurement precision. This translates to not using an intentionally defocused observing strategy during full moon (unless an I-band filter is used). Some of the reasons for these precautions will be better understood after reading the following chapters.

Precaution when Focusing the Mirror

Focusing is accomplished in one of two ways: moving the primary mirror or moving the CCD camera assembly. The latter is preferable. However, because I removed the “microfocuser” from my Meade LX200GPS telescope (in order to clear the base for reaching the north celestial pole as part of the pointing calibration), my focusing is accomplished by moving the primary mirror. This is a crude way to focus, and it causes problems for exoplanet observing. The remainder of this section should serve as a warning about focusing with the primary mirror.

The primary mirror is moved in or out using a rod attached to reducing gears attached to the focusing knob. When making an adjustment in a direction opposite to the previous one the mirror will not move until a hysteresis range of movement is overcome. For my telescope this is approximately a half turn of the focus knob (or 5 turns when using a 10:1 gear reducer). Since my focusing is accomplished using a wireless MicroTouch focusing unit (sold by Starizona) the hysteresis for reversing direction amounts to ~650 steps (of a stepper motor attached to the focus knob’s 10:1 reducer shaft). I try to avoid reversing direction for two reasons: 1) the mirror changes tilt enough to cause image shift, and 2) the hysteresis amount is not exactly the same for each reversal of direction so I can never achieve an accurate adjustment with one command when a reversal of direction is involved.

Before explaining the strategy I’ve adopted for this problem I should describe results of my measurements of desired focus setting (in absolute position readout counts) versus temperature and elevation angle. It is believed that the most important cause for needing to make a focus change is the telescope’s change in temperature. As a telescope cools the tube shrinks, and this requires that either the CCD assembly must be moved out or the mirror must be moved “in.” For my telescope there is an additional factor contributing to the need for focus adjustment: elevation angle. I’ve produced a plot of desired focus setting versus elevation angle for a selection of temperatures. For a typical observing session the elevation angle effect is more important than temperature effects. Moreover, due to hysteresis there is a different set of desired focus setting traces for “inward” versus “outward” adjustments, and they are offset by the hysteresis amount (the 650 steps mentioned above).

“Inward” focus adjustments are required when temperature cools with time during an observing session. After transit the changing elevation angle also requires “inward” focus adjustments. Thus, after transit I can count on all adjustments to be in the same direction, “inward” (unless I’ve over-corrected and have to back-up). Observations before transit may require focus adjustments in either direction, depending on the relative importance of elevation changes versus temperature changes. Usually, elevation changes dominate, and this requires “outward” focus adjustments. Because I can anticipate the direction of focus adjustments during an observing session (based on whether the object will be rising or setting) I begin an observing session with a focus setting that was achieved going in the same direction as I anticipate will be required by subsequent adjustments. This precaution assures that I am unlikely to encounter a large hysteresis adjustment (until transit).

The problems associated with having to adjust focus using the mirror, instead of a microfocuser that moves the CCD assembly, are so troublesome that I question the wisdom of removing the microfocuser. The principal reason that prompted me to do this was the need for providing sufficient clearance of the “optical backend” in relation to the mounting base that I could point to the north celestial pole in order to calibrate pointing. The LX200GPS “loses” pointing calibration so often that this became an over-riding consideration. Perhaps Meade will some day improve their firmware quality control, so that pointing calibration will not be “lost” between observing sessions. When this happens I would recommend the use of Meade’s microfocuser and forsake the ability to observe north of ~75 degrees declination.

I’ve “belabored” this focusing problem partly to serve as a warning to any observer who is considering focus adjustments using the primary mirror. I also hope I have illustrated the merits of buying a telescope having a tube made with low thermal expansion material.

The focusing problems just described in excessive detail would not be tolerated in a professional telescope. We amateurs, with limited budgets, must spend extra effort on such matters. When using amateur hardware in an attempt to perform professional quality observations, whatever is saved in hardware investment cost is paid for with an extra workload.

─────────────────────────────────

Chapter 9

Autoguiding

─────────────────────────────────

Some CCD cameras have two chips, a large main one for imaging and a small one beside it for autoguiding. CCDs with just one chip can be autoguided if a separate CCD camera is attached to a piggy-backed guide telescope. If you have neither of these ways to autoguide, may I suggest that you consider a hardware upgrade.

My CCD camera is a Santa Barbara Instruments Group (SBIG) ST-8XE. The X and E at the end just signify that I’ve upgraded a ST-8 to have a larger autoguider chip (SBIG’s TC237) and USB communication.

There are a couple ways to automatically autoguide for an entire observing session. One is to use the autoguider chip to nudge the telescope drive motors. This can be done whether the autoguider chip is in the same CCD camera as the main chip or on a separate CCD camera attached to a piggy-back guide telescope. The main drawback for this method is that the telescope drive motors have hysteresis, especially the declination drive, and this produces uneven autoguiding. This method at least keeps the star field approximately fixed with respect to the pixel field (assuming a good polar alignment), but it won’t sharpen images.

Image Stabilizer

The second method for autoguiding is to use a tip/tilt mirror image stabilizer. I have an SBIG AO-7 tip/tilt image stabilizer. For large CCD format cameras SBIG sells an AO-L image stabilizer. As far as I know SBIG is the only company selling an image stabilizer that’s priced for amateurs. The AO-7 allows me to use the autoguider image to adjust a tip/tilt mirror at the rate of up to ~10 Hz, depending on how bright a star I have in the autoguider’s FOV. When the required mirror movement exceeds a user-specified threshold (such as 40% of the range of mirror motion) the telescope is nudged in the appropriate direction for a user-specified preset time (such as 0.1 second). I use MaxIm DL for both telescope control and CCD control, and I assume other control programs have the same capability.

In the planning chapter I described choosing a sky coordinate location for the main chip that assures the autoguider’s FOV includes a star bright enough for autoguiding. Using a 14-inch telescope a star with V-mag ~ 11 is acceptable for 5 Hz autoguiding when using an R-band filter. If the brightest star that can be placed in the autoguider’s FOV is fainter, it may be wise to consider observing with either a clear filter or a blue-blocking filter (described in Chapter 14). My CCD with a photometric B-band filter produces star fluxes that are only 16% of flux values produced by an R-band filter (by a typical star), so a star would have to be 2 magnitudes brighter to be useable for B-band autoguiding.

With an SBIG tip/tilt image stabilizer it is usually possible to produce long-exposure images that are as sharp as those in the average short-exposure, unstabilized images. Tracking is possible for the entire night provided cirrus clouds don’t cause the autoguide star to fade significantly.

Image Rotation and Autoguiding

As pointed out earlier, whereas a successful autoguide observing session that lasts many hours will keep the autoguider star fixed to a pixel location on the autoguider chip, if the telescope mount’s polar axis is imperfectly aligned the main chip’s projected location on the sky will rotate about the autoguide star during an autoguided observing session. This will be seen in the main chip images as a star field rotation about an imaginary location corresponding to the autoguider star. Each star will move though an arc whose length will be greater for stars farthest from the autoguider’s guide star. The main chip’s FOV will change during the observing session, and any reference stars near the FOV edge are at risk of being “lost.” An important goal of exoplanet transit observing is to keep the star field viewed by the main chip fixed with respect to the main chip’s pixels. Therefore, autoguiding will be most successful if the mount’s polar axis is aligned accurately.

Observer Involvement with Monitoring

Amateurs have different philosophies about how much attention must be given to observing during an observing session. Some prefer to start the entire process with a script that controls the various control programs. I prefer a greater presence in the control room throughout the observing session. After the flats have been made, and an observing sequence has been started, it may be theoretically possible to go to bed with an alarm set for the end of the session. I like to spot check such things as auto-guiding, focus setting, seeing, extra losses, CCD cooler setting, and record items in an observing log at regular intervals. After all, if a passing cirrus cloud causes the autoguider to lose track, the following observations will be useless until the observer reacquires the autoguider star. Autoguiding needs are the main reason I stay involved with observing for the entirety of an observing session. As you may have gathered from my “observatory tour” (chapter 2) my observing control room is comfortable. This is primarily in response to the requirements of autoguiding, which requires that I check-in on the telescope’s tracking and record things on the observing log at frequent intervals.

─────────────────────────────────

Chapter 10

Photometry Aperture Size

─────────────────────────────────

Before describing how images can be processed to produce light curves it is necessary to have an understanding of some basic concepts related to photometry aperture size.

The following descriptions will be based on my use of MaxIm DL, or MDL as I will refer to the program. I’ve never used other image analysis programs that are supposed to be comparable, but I’ll assume that they’re capable of performing similar operations. It will be up to the user of another program, such as AIP4WIN or CCDSoft, to figure out the equivalent procedure. I don’t want this paragraph to seem like an advertisement for MDL, but I do want to say that I’ve never encountered anything related to image manipulation that I needed to do for photometry that wasn’t performed easily with MDL.

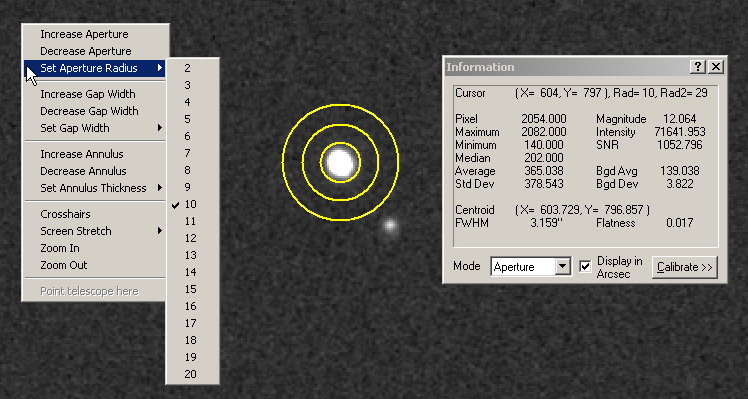
Figure 10.01. Three aperture circles with user-set radii of 10, 9 and 10 pixels. The Information window gives the cursor location, the radius of the signal circle (10 pixels) as well as the radius of the sky background annulus outer circle 29 pixels). The Information window shows many other things, such as magnitude, star flux (labeled “Intensity”), SNR and FWHM.

MDL uses a set of three circles for performing aperture photometry measurements. Figure 10.01 shows photometry aperture circles centered on a star. Notice that in this image the central circle, which I shall refer to as the “signal aperture,” appears to enclose the entire pixel area where the star’s light was registered. Note also that the outer sky background annulus (the area between the outer two circles) is free of other stars. When these two conditions are met the star flux reading displayed in the Information window (labeled “Intensity”) will be valid. If the signal aperture is too small the flux reading will be too small, and if the signal aperture is too large the flux may be correct but it will have a larger component of noise due to the many pixels involved. With a too large signal aperture the pixels near the outer edge will contain no information about star flux, but they will contribute noise to the flux reading. This can be easily seen by changing the signal aperture size and noting the way SNR changes, as shown in the next figure.

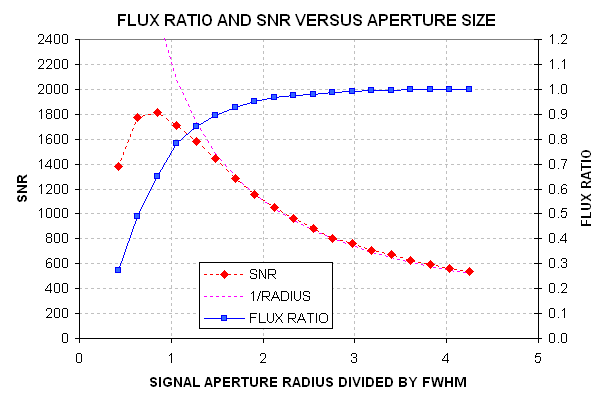
Figure 10.02. SNR and flux ratio (“aperture capture fraction”) versus signal aperture radius (normalized to FWHM) for the star in the previous figure. The purple dotted trace is “1 / radius.”

This figure shows a maximum SNR when the aperture radius is about ¾ of the FWHM. This agrees with theoretical calculations for a Gaussian shaped PSF. There are good reasons for not choosing a signal aperture radius where SNR is maximum, at least for exoplanet light curve work. Notice that when the maximum SNR size is chosen the photometry aperture circle captures only ~ 65% of the total flux from the star. This is easily understood by considering that as the radius is increased more pixels are used to establish the star’s flux, but these new pixels are adding parts of the star’s PSF that are less bright than the central portion. Although the new pixels are adding to the total flux, they are also adding to the noise level of the total flux. This happens because each pixel’s count value is compared with the average count value within the sky background annulus, and a difference is added to the total flux. But each pixel is “noisy” (due to thermal jostling of electrons in the CCD elements and electronics, read noise and sky brightness contributions to the counts from each pixel). For example, in this image the RMS noise for each pixel is 3.5 counts. The noise level of the total flux increases with the square-root of the number of pixels added, and since the number of pixels increases as the square of the radius the noise on total flux readings should be proportional to the signal aperture radius. Beyond a radius of ~1.4 × FWHM, where total flux has essentially reached an asymptote, the SNR decrease as 1/radius.

For some observing projects small signal apertures are appropriate, such as detecting and tracking faint asteroids. For the asteroid situation SNR could be 2 to 3 and brightness precision isn’t important. But consider some of the problems that might occur with bright stars where brightness precision is paramount. In Chapter 8, describing focus drift, it was shown that when PSF changes during an observing session “aperture capture fraction” may differ across the image.

This is a situation in which the user faces competing goals: the desire for small stochastic noise levels versus small systematic errors. If we adopt an aperture radius of twice FWHM the aperture capture fraction rises to 96% but SNR is reduced to ~60% of its peak value. Even this may be too risky. Consider the implications of one part of an image having a PSF for which this aperture captures 95% of the total flux versus 96% at the center. This 1% difference corresponds to 10 mmag, and if our goal is to eliminate systematic errors above the 2 mmag level, for example, then we cannot tolerate 1% changes in the aperture capture fraction for the target star, or any of the reference stars, during the entirety of the observing session. By choosing a radius that is 3 times FWHM, ~99% of the total flux is captured. I feel comfortable with this choice, but there’s no clear way of arguing for a best aperture size since each observing session is different and one might be absolutely OK using a small aperture while another would be riddled with intolerable systematic errors.

My subjective solution to this problem of not knowing how small a signal aperture is acceptable is to process the images using 2 or 3 aperture sizes. As Chapter 12 describes, MDL can easily produce ASCII files of flux measurements with different aperture sizes, so this is one option to consider – especially in those cases where image sharpness varies greatly from image to image or from image center to the edges.

There’s more to choosing photometry apertures than the concern about aperture capture fraction. The same image in Fig. 10.01 has a bright star (not shown in this figure) that would be useful to use as a reference star, but a fainter star is located 9 ”arc (12 pixels) away. The next figure’s left panel shows these stars with a photometry pattern for which the signal aperture radius is 3 × FWHM. This aperture choice is unacceptable because some of the nearby star’s flux is within the signal aperture. The right panel shows that the nearby star can be excluded from the signal aperture by reducing the aperture radius from 12 pixels to 10 pixels, corresponding to 2.4 × FWHM. Before choosing a signal aperture radius it is important to check all bright stars to see if a radius adjustment like this one should be made.

Figure 10.03. Left panel: Candidate reference star showing photometry aperture circles with the signal aperture radius = 3 × FWHM. Right panel: Same star with signal aperture radius = 2.4 × FWHM.

What about stars in the sky background annulus, as shown in the next figure?

Figure 10.04. Example of a star with a nearby star that’s within the sky background annulus.

Actually, this is not a problem because MDL’s photometry tool uses a sophisticated algorithm for eliminating outlier counts in this annulus. AIP4WIN does the same using a different algorithm. (Note: The current version of MDL’s “on the fly” photometry doesn’t use the sophisticated algorithm for rejecting sky background counts from such stars, so be careful when using the MDL Information Window’s “Intensity” readings.)

In conclusion, the most important aperture size to choose carefully is the signal aperture radius. Whenever there’s concern about what aperture size to choose it is very easy (in MDL) to process the images with several choices. The files produced with different aperture sizes can be imported to different spreadsheets, as described in Chapter 13, and systematic behaviors of each star can be performed to determine which aperture size to accept.

This chapter’s message is to start with a default signal aperture radius = 3 × FWHM, and adjust in response to the presence of interfering stars. Consider using 2.5 × FWHM and 3.5 x FWHM. Only the “brave” or “foolhardy” will use 2 × FWHM for precision photometry.

─────────────────────────────────

Chapter 12

Image Processing

─────────────────────────────────

The morning after a long observing session may require as little as an hour to perform a good quality analysis resulting in a light curve, or it may take much longer. Many factors dictate how much effort is required to perform the tasks described in this and the next chapter.

The task of converting images to a light curve consists of two parts: 1) processing images to acquire star fluxes for several stars from many images, and 2) converting these star fluxes to a light curve using a spreadsheet. This chapter deals with the first part, processing images and creating files of star fluxes that can be imported to a spreadsheet for performing the second analysis part. Please view the specific instructions as merely one way to deal with issues that you will want to deal with using whatever tools you feel comfortable using. My examples will be for the MaxIm DL (MDL) user, so if you use another image processing program you’ll want to just glean concepts from my explanations.

Imagine that we have 450 raw images from a night’s observations. This could be from a 6.5-hour observing session consisting of 60-second exposures. Given that my RAM is limited to 1 GB there are limits to how many images I can load without having to use virtual RAM (which really slows things down). By setting MDL to disable the “undo” feature it is possible to work with twice as many images in working memory. My CCD has pixel dimensions of 1530 x 1020, and a 1x1 (unbinned) image uses 1.1 Mb of memory (compressed). I can easily load 150 raw images into working memory without involving virtual RAM. This is 1/3 of the 450 images to be processed, so what I’ll describe in the next few paragraphs will be done three times. Each user will have a different limit for the maximum number that can be loaded into working memory, so if you want to use MDL and the following processing procedure you will simply have to determine how to replace my use of “150 images” with whatever applies to your computer’s capabilities.

The first step is to calibrate the 150 images using the master dark and master flat frames. For the rest of this chapter I’ll present a detailed version of how to do something using MDL in smaller font. So the next paragraph describes in more detail how I prefer to calibrate the images in working memory using MDL.

[Specify the master flat and master dark files in MDL’s Set Calibration window. Select “None” for “Dark Frame Scaling” (since the dark frame is at the same temperature and has the same exposure as the light frames to be calibrated). Check the Calibrate Dark and Calibrate Flat boxes. Don’t check “bias.” Exit the calibration set-up and calibrate all 150 raw images (~10 seconds).]

The second step is to “star align” all 150 images. This will consist of x and y offset adjustments, as well as image rotations if necessary.

[Invoke MDL’s Align command and select Add All images. The Align Images window appears; select “Auto – star matching” and click “OK” to align all images. The result (after ~1.5 minutes) will be a set of images in working memory that have been shifted in x and y, and rotated if necessary, to achieve alignment of the star field, using the first image in the list as a template. This set of images might be worth saving to a directory, but that’s optional (to do this with MDL, select File/BatchSave&Convert, etc).]

The third step is to add an artificial star in the upper-left corner of all images. This is done using a free plug-in written by Ajai Sehgal. You can get a 32x32 pixel version from the MDL web site; the 64x64 version was written at my request and you may either ask Ajai or me for it to be sent by return e-mail as an attachment, or download it from the web site http://brucegary.net/book_EOA/xls.htm. I prefer to use the 64x64 version since it allows the use of large photometry apertures. The artificial star will be Gaussian shaped with the brightest pixel equal to 65,535 and a FWHM = 3.77 pixels.

[With MDL, the artificial star is added to all images by opening the Plug-In menu and clicking “Add 64x64 reference star.”]

As an aside, consider what we have in working memory now: 150 images, all stars are at the same pixel locations, including an artificial star with a fixed star flux in all images. If we compare the flux of a star with that of the artificial star, and convert that to a magnitude difference, we have a way of keeping track of the star’s brightness in all images that has the added feature of retaining more information than simple “differential photometry.” With differential photometry the user specifies a reference star (or stars, for ensemble differential photometry), and all object stars and check stars have their fluxes compared to the reference star (or the average of the reference stars when doing ensemble). The flux ratios are converted to magnitude differences, and a file is created that contains these magnitude differences. For some users the appeal of this set of magnitude differences is that changes in extinction, or changes in cirrus cloud losses, are removed - to first order. Or, to put it another way, information about extinction and cirrus losses are “lost” when recording a standard differential photometry file. There’s a serious disadvantage in processing images this way; it may not be important for variable star work but it’s often important for exoplanet LCs: if any of the stars used for reference are variable you could remain clueless about it, and if you somehow suspected that the reference star was not constant you would have to repeat the image processing with a different star designated for use as the reference. The value of using the artificial star for reference is that extinction and cirrus losses are retained in the recorded file, while also retaining magnitude differences between stars! When the magnitude differences file is imported to a spreadsheet the user will have full control over which stars to choose for use as reference. The user can view all stars that were measured and evaluate their constancy, and be guided by this analysis in choosing which stars to use as a final ensemble reference set. This requires extra work for the user, but with the extra effort comes a significant increase in “analysis power” – as the next chapter will illustrate.

The next step is to invoke the image analysis program’s “photometry tool” in order to create a file containing star magnitudes (relative to the artificial star) for the 150 images. Before proceeding with this you will need to carefully choose photometry circle sizes, as described in Chapter 10. If you are unsure about the best signal aperture radius, create files for each of several plausible signal aperture sizes.

[Using MDL, invoke the photometry tool (Analyze/Photometry). All images in working memory are selected by default in the “Image List” and the highlighted image in this list is displayed in the work area. Check the boxes labeled “Act on all images” and “Snap to centroid.” Open the drop down menu “Mouse click tags as:” and select “New Object.” Navigate around the highlighted image and find the exoplanet star; left-click it. The aperture circles appear and are snap-centered on the star; the “Obj1” label is displayed (it can be dragged to an “out of the way” location nearby if the label overwrites stars to be measured). You may not notice it, but all images have the same photometry circles centered on the same star (you can check this by highlighting an image in the “Image List” to see that image highlighted in the work area). Next open the drop down menu “Mouse click tags as:” and select “New Reference Star.” Navigate to the artificial star in the highlighted image and left-click its approximate location; the set of photometry circles appear snap-centered over the artificial star with the label “Ref1”. All images automatically have their reference star identified with the same aperture circles and “Ref1” label. Next, open the drop down menu “Mouse click tags as:” and select “New Check Star”. Navigate the highlighted image to the first star chosen earlier to be the first in the series of “check stars” – to be considered for use as reference stars during the spreadsheet phase of analysis. Left-click this star, and proceed to do the same for the rest of the check star list. Finally, click the “View Plot…” button. The “Photometry” graph appears. It can be resized to exaggerate the magnitude scale if you want to see if any of the stars are variable or noisy. This encompasses a large magnitude range, so small variations won’t be visible, but it’s worth a cursory look. The real purpose for displaying this graph is that it has a “Save Data…” button. Click it and navigate the directory structure to where you want to record the magnitude differences CSV-file. Enter a file name, such as “1_r” (where r is the signal aperture radius), and click “Save”. If other signal aperture sizes are of interest, right-click on an image and a drop-down menu will appear that allows you to change the radius. The photometry for all images is immediately recalculated; click the graph’s “Save” button and save the CSV-file with another descriptive name, such as 1_r, where the value for r is different. When finished creating CSV-files for all the signal apertures of interest, click “Close” and you’re back to MDL’s main work area. All files in working memory may be deleted (alt-F, E).]

Perform the above analysis with the other two groups of 150 raw images. Use different CSV-filenames, of course, such as “2_r” and “3_r” – where the “r” stands for the signal aperture radius. If more than one signal aperture is used the CSV-file names could look like the following: 1_10, 2_10, 3_10 for the 10-pixel radius photometry, and 1_12, 2_12, 3_12 for the 12-pixel radius photometry, etc.

This completes the image processing phase of analysis.

─────────────────────────────────

Chapter 13

Spreadsheet Processing

─────────────────────────────────

I hope you’re somewhat familiar with spreadsheets. I use Excel, which I think can be found on every computer using a Microsoft operating system. If you use a different spreadsheet then you’ll have to translate my instructions to whatever is needed by your spreadsheet.

Let’s assume that after doing the image processing described in the last chapter we have 3 CSV-files. They’re in ASCII (i.e., text) format, and the data lines will look something like the following:

"T (JD)","Obj1","Ref1","Chk1","Chk2","Chk3","Chk4","Chk5"

2454223.6114930557,2.013,0.000,4.197,2.956,2.132,3.993,2.441

2454223.6122800927,2.012,0.000,4.238,2.943,2.124,3.966,2.423

2454223.6130555556,2.002,0.000,4.192,2.941,2.114,3.983,2.418

2454223.6138310186,2.008,0.000,4.203,2.934,2.110,3.967,2.426

2454223.6146064815,2.007,0.000,4.186,2.955,2.118,3.961,2.427

2454223.6153935185,2.002,0.000,4.191,2.937,2.110,3.969,2.423

Each row corresponds to an image. The first image has a JD time tag corresponding to mid-exposure time. The next value (2.013 for the first image) is the magnitude difference between the “object” (the exoplanet) and the artificial star. The next value is zero because this is the magnitude of the artificial star referred to itself. Then there are 5 magnitude differences for the so-called “check” stars used in this example.

The next step is to import the CSV-file to a spreadsheet.

Figure 13.01. Screen capture of a spreadsheet that calculates air mass after importing the CSV-file when the cursor is at cell B7. Columns B through I contain CSV-file magnitude difference data. Columns Z through AG calculate AirMass, displayed in column Y.

Since this screen shot is barely readable the next figure is presented showing only the left-most columns, where data is imported.

Figure 13.02. Screen capture of the part of the spreadsheet where the CSV-file has been imported. The user must enter site coordinates in cells C4:C5 and object RA/Dec in cells H4:J5.

Air mass (AirMass) is calculated using JD, site coordinates and the target’s RA and declination. The next figure shows the right-most section, where air mass is calculated.

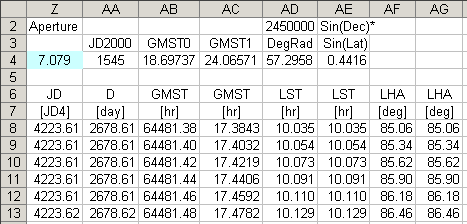
Figure 13.03. Screen capture of the part of the spreadsheet where air mass is calculated from the JD in column B, and site coordinates and object RA/Dec.

Appendix C contains a description of the algorithm that is used to calculate air mass. An easier way to have this capability is to download a sample spreadsheet from http://brucegary.net/book_EOA/xls.htm.

The user then imports the other two CSV-files to the spreadsheet, below the previous one (and deletes title lines). A better procedure is to concatenate the three CSV-files to one CSV-file (using Windows Notepad), then import this one CSV-file to the spreadsheet.

The next spreadsheet page is devoted to plotting an extinction curve. It copies contents from the first page, converts JD to UT and does other things. Here’s a screen shot of the left half of this page.

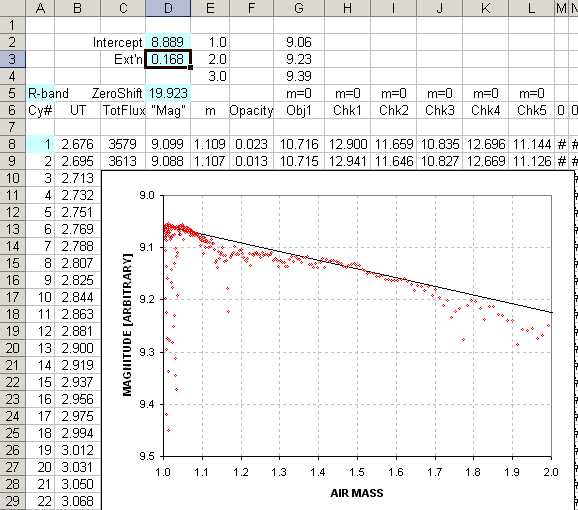
Figure 13.04. Left side of the second spreadsheet page. The columns and graph are explained in the text.

Column B is UT (based on the first page’s JD). Column C is total flux (based on the first page’s check star magnitudes, converted to flux, and added together). Column D is a magnitude corresponding to total flux. Column E is air mass (copied from the previous page). The graph plots columns D versus E. The fitted slope is based on user entered values for zenith extinction (0.168 in this example) and zero air mass intercept (8.889). Column F is “unaccounted for extra opacity” based on the difference between total magnitude and the extinction model (the next figure shows the right side of this page, which includes a plot of opacity versus time). Columns G through L are extinction-corrected magnitudes for the exoplanet and check stars.

Figure 13.05 (next page) shows the right side of this spreadsheet page. The graph is for “extra” opacity (unaccounted for by the simple extinction model) versus UT and air mass versus UT. Columns AC through AG are image magnitude corrections based on each star’s measured magnitude versus its extinction-corrected magnitude. If there were no clouds, or dew losses, or bad seeing losses (either atmospheric or related to the wind shaking the telescope), these columns would be zero (plus stochastic noise). Column AV is a median combine of columns AC through AG (the check stars). The user is free to choose from any of the check star columns for creating column AV. This column is a refinement of the “extra losses” column, and will be used on the next spreadsheet page to adjust the “object” (exoplanet) column of magnitudes.

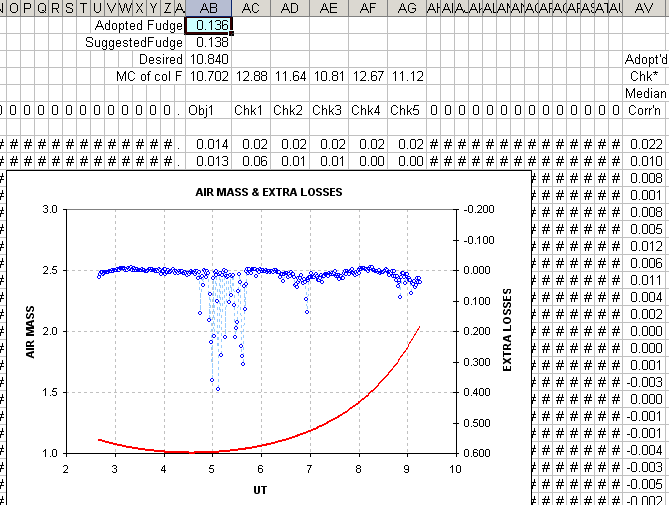
Figure 13.05. Right side of second page. The column explanations are in the text.

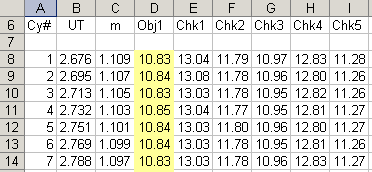
Figure 13.06. Left side of third spreadsheet page, explained in the text.

In Fig. 13.06 the D column is the “object’s” magnitude corrected for extinction (using the model for extinction and air mass) and also corrected for “extra losses” (column AV on the previous page). Columns E through I are the corresponding versions for the check stars. In a perfect world the values in each row of a column would the same. Here’s a plot of the corrected magnitudes.

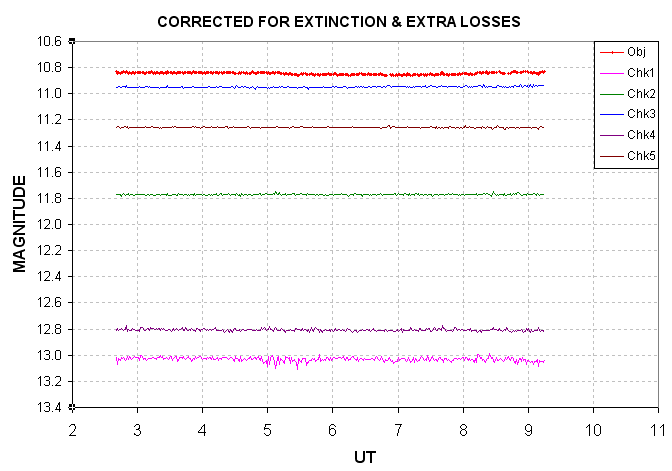
Figure 13.07. Plot of magnitudes corrected for extinction and “extra losses.”

In viewing this plot (stretched vertically) it is often possible to identify check stars that are “poorly behaved.” Poor behavior could be variability on a time scale shorter than the observing session length (yes, you do encounter such stars). Poor behavior could also be noisiness (due to poor SNR), or occasional spikes (due to cosmic rays). Another form of bad behavior would be trends related to image rotation (more common for stars located near a corner where rotation effects are larger). From this figure we learn that the only star to be avoided is the faintest one, “Chk1.” After noticing this, the user should revise the cells in the previous page’s AV column to omit the Chk1 column, thus using for “ensemble reference” the stars Chk2, Chk3, Chk4 and Chk5.

The ability of the user to choose which stars to use for reference, based on a graph of their behavior, is the best reason for using this analysis procedure.

Another important feature of this analysis procedure is that it provides an objective and automatic way for removing data associated with high “extra losses.” The threshold for acceptable “extra losses” can be set by the user. For example, I typically accept “extra losses” smaller than 0.1 magnitude.

Outlier data can also be removed using the same concept of a user-specified threshold. The threshold should depend on SNR, since faint objects will have greater internal scatter. For identifying outlier data I use the difference between a value and the 4 nearest neighbors. A histogram of these “neighbor differences” will have a Gaussian shape, and it is easy to adjust two parameters to fit the main part of the Gaussian, as illustrated in the next figure. Outliers will show themselves in the histogram as unlikely events far out in the wings. This is one way to establish an outlier rejection criterion.

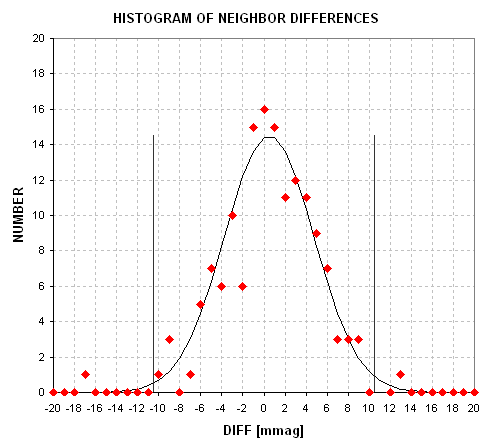
Figure 13.08. Histogram of “neighbor outlier” data with a Gaussian fit. The two vertical lines are the user-specified rejection criteria.

For stars with R-mag ~11, which is the case treated in this chapter, I would typically reject data that exceeds 11 mmag (shown in the above figure). For this “case study” the extra losses criterion led to the automatic removal of 5% of the data, and the “outlier” criterion led to the removal of an additional 3%.

Figure 13.09 is the final light curve. In this figure the small red dots are from individual 60-second images that passed the acceptance criteria for both “extra losses” and outlier rejection. The large red circular symbols are 9-point, non-overlapping, median combines of the accepted data (red dots). At the top of the panel are two vertical lines indicating the predicted times for ingress and egress. In the lower-right corner is a notation of which reference stars were used. The upper-left note states that a 13 pixel aperture radius was used for measuring star fluxes and this led to an RMS for 1-minute data of 4.1 mmag, which corresponds to RMS for 5-minute averages of 1.85 mmag.

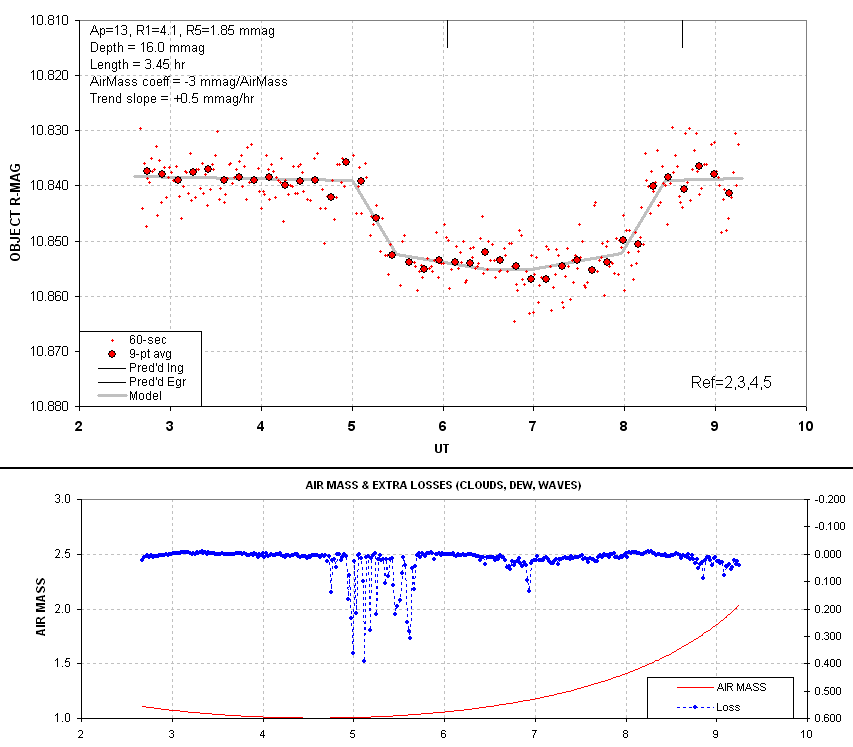
Figure 13.09. Light curve of a 11^th magnitude exoplanet candidate using an R-band filter. The explanation of this figure is in the text.

The model lines are for a general-purpose transit. The transit model consists of 5 parameters, which are adjusted by the user: ingress UT, egress UT, depth at mid-transit, fraction of time spent during ingress (or egress) in relation to the time from ingress to mid-transit, and ratio of depth at completion of ingress (or start of egress) to the mid-transit depth. Note that the parameter for the fraction of time spent during ingress is a good approximation to the ratio of the exoplanet’s radius to the star’s radius (assuming a close to central transit chord).

An important additional feature of the transit model is that it provides a way to accommodate curvature due to a temporal trend and a correlation with air mass. The temporal trend term is a simple coefficient times UT, which in this case is +0.5 mmag times UT (hinged at UT = 6). The trend is most likely produced by image rotation (imperfect polar alignment) that causes stars to move across pixel space during the entire observing session. If the master flat frame was perfect there shouldn’t be such a term, but no flat field is perfect.

The air mass term is a coefficient times “air mass minus one.” For this case I chose an air mass coefficient of -3 mmag/airmass. This term is required when stars are used for reference that are not exactly the same color as the object (as explained in the next chapter). The trend and air mass terms are adjusted using the “out of transit” (OOT) portions of the light curve.

For this light curve the time spent by the secondary body to complete an ingress (contact 1 to contact 2, also the same as the time to complete an egress, contact 3 to contact 4) is 17% of the time spent for the center of the secondary body to traverse the chord for its path across the primary star. Thus, the secondary has a radius that is 17% the radius of the star. That’s interesting! If the secondary is an exoplanet, and has a radius 0.17 times the star’s radius, it should block 2.9% of the star’s light, producing a 29 mmag deep transit. Yet, we see only 16 mmag. This must mean that another star is within the signal aperture, adding almost as much R-band light as the star undergoing transit. Appendix D has a more extensive discussion of ways to interpret light curves.

The next chapter treats the important matter of light curve baseline curvature produced by the use of reference stars having a different color than the transited star.

─────────────────────────────────

Chapter 14

Star Colors

─────────────────────────────────

For LC analyses of variable stars, where the goal is to measure changes with precisions of ~ 10 to 50 mmag, it is common practice to use as many reference stars as possible in an ensemble mode. For eclipsing binaries, which have deep transits, this is also an acceptable practice. But when the transit depth is less than ~ 25 mmag, as any exoplanet transit will be, it matters which stars are used for reference. The problem arises when the target and reference stars have different colors. This is because a red star exhibits a smaller atmospheric extinction compared to a blue star, regardless of the filter used.

Atmospheric Extinction Tutorial

We need to review some basic atmospheric extinction theory in order to better understand why star color matters. The atmosphere has three principal extinction components (in the visible region): 1) Rayleigh scattering by molecules, 2) Mie scattering by aerosols (dust), and 3) resonant molecular absorption (by oxygen, ozone and water vapor). The first two components are more important than the third. The Rayleigh scattering component is shown in the next figure.

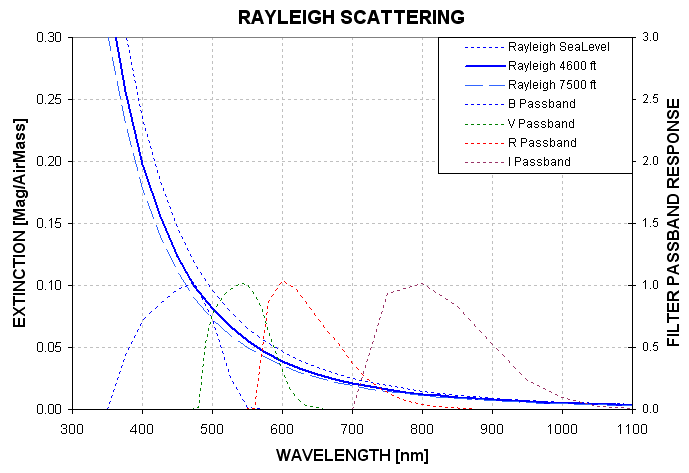
Figure 14.01. Atmospheric Rayleigh scattering at wavelengths where CCD chips are sensitive for three observing site altitudes. Filter spectral response shapes are shown for B, V, R and I (Custom Scientific BVRcIc filters and KAF1602E CCD chip, normalized to 1). The Rayleigh scattering model is based on an equation in Allen’s Astrophysical Quantities, 2000.

Notice how much Rayleigh scattering varies throughout the B-filter response region; the greatest scattering (at 350 nm) is 5 times the smallest (at 550 nm)!

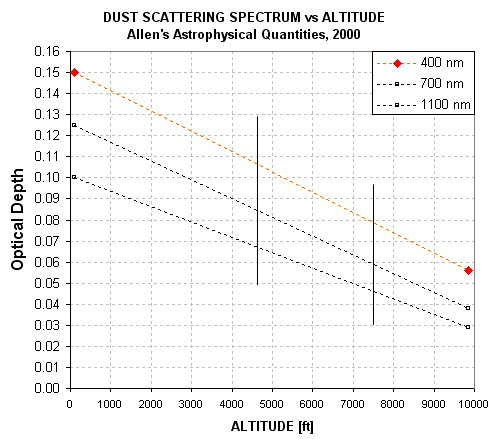
Figure 14.02. Atmospheric aerosol (dust) Mie scattering versus observing site altitude for three wavelengths (based on a global model by Toon and Pollack, 1976, cited in Allen’s Astrophysical Quantities, 2000).

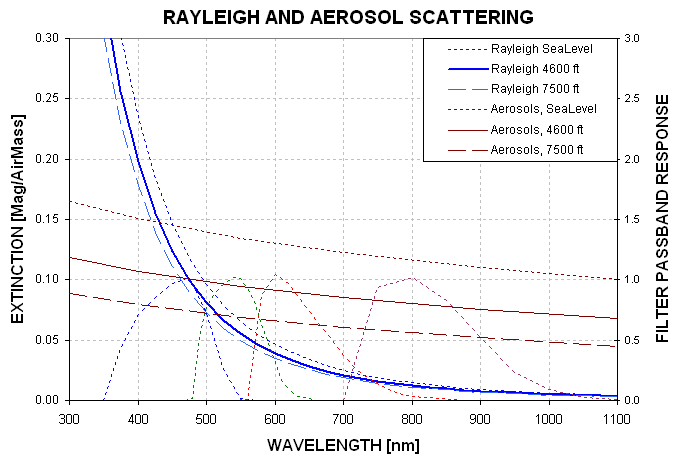
Figure 14.03. Atmospheric Rayleigh and aerosol Mie scattering versus wavelength.

Figure 14.02 shows aerosol Mie scattering (it is customary for “Mie scattering” to refer to the situation of the particle circumference being much greater than wavelength). It’s a plot of aerosol scattering versus altitude for 3 wavelengths. A model fit to this data allows for the conversion to scattering versus wavelength for specific altitudes. This is shown in Fig. 14.03. This figure also includes the Rayleigh scattering component, and it should be noted that for B-band both scattering components are about the same. For I-band the only scattering component that’s important is aerosol Mie scattering.

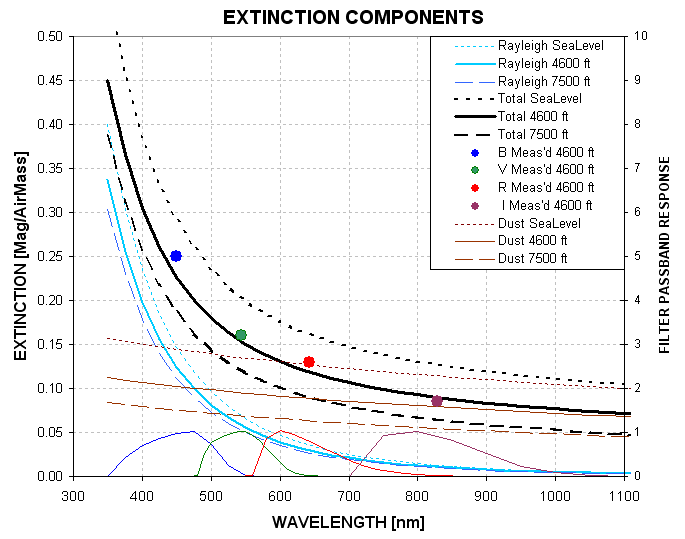
Figure 14.04. Atmospheric total extinction components (Rayleigh scattering and aerosol scattering). Typical measured extinction coefficients for my site at 4660 feet are shown as large filled circles (seasonal average).

At my observing site (4660 ft) the yearly-average measured extinction values (large colored dots in Fig. 14.04) agree with the model (thick black trace). It should be remarked that the Rayleigh component at a given site will vary by only small amounts (related to barometric pressure) whereas the aerosol scattering component can vary by large amounts. The seasonal variation of extinction is therefore related to aerosol changes. Volcanic ash lofted to the stratosphere, where it will reside for many months, can produce large temporary aerosol scattering events. Using this graph it should be possible to use I-band extinction to infer extinction at the shorter bands. The opposite is less true; it’s difficult to infer I-band extinction from a B-band extinction measurement (since B-band extinction is dominated by Rayleigh scattering).

My purpose in presenting this atmospheric extinction tutorial is to sensitize you to the slopes of extinction within a filter band pass.

So what? How can the extinction slope within a given filter band possibly affect differential photometry measurements? We now need to review some stellar blackbody spectrum theory.

Blackbody Spectrae and Filter Band Passes

Hot stars shine mostly in the blue, whereas cools stars shine mostly in the red, as the following graph shows.

Figure 14.05. Blackbody spectral shape versus temperature (4500 K to 8000 K). T = 4500 K corresponds to spectral class K3 and 8000 K corresponds to A2.

Notice that not only do hot stars radiate more photons at every wavelength region, but the difference is greatest at short wavelengths.

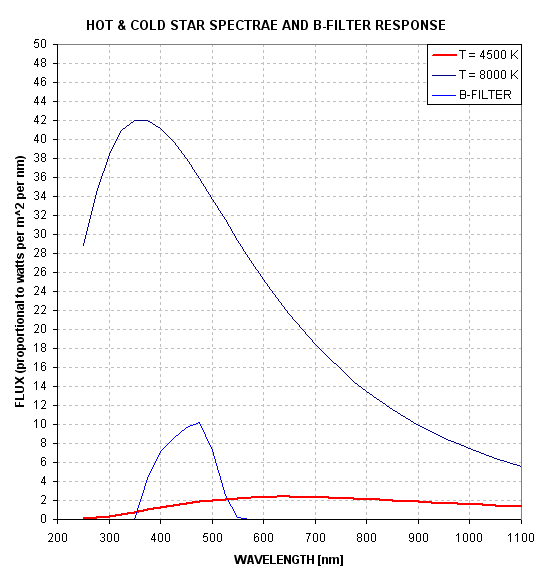
Figure 14.06. B-filter response and spectral shapes of hot and cold stars.

Notice in Fig. 14.06 that within the B-band response a cool star radiates less and less going to shorter wavelengths, whereas it is the reverse for the hot star. The effective wavelength for a cool star is 467 nm whereas for a hot star it is 445 nm. The more interesting parameter for light curve systematics is the equivalent zenith extinction coefficient for the two stars. For the cool one it’s 0.228 mag/airmass whereas for the hot star it’s 0.244 mag/airmass (I use the term “airmass”, “AirMass” and “air mass” interchangeably). In other words, a cool star’s brightness will vary less with airmass than a hot star, the difference being ~0.016 mag/airmass.

Effect on Light Curves of Reference Star Color

Consider an observing session with a B-band filter that undergoes a range of airmass values from 1.0 to 3.0. Consider further that within the FOV are two stars that are bright, but not saturated; one is a cool star and the other is hot. The magnitude difference between the two stars will change during the course of the observing session by an impressive 32 mmag! This is shown in the next figure.

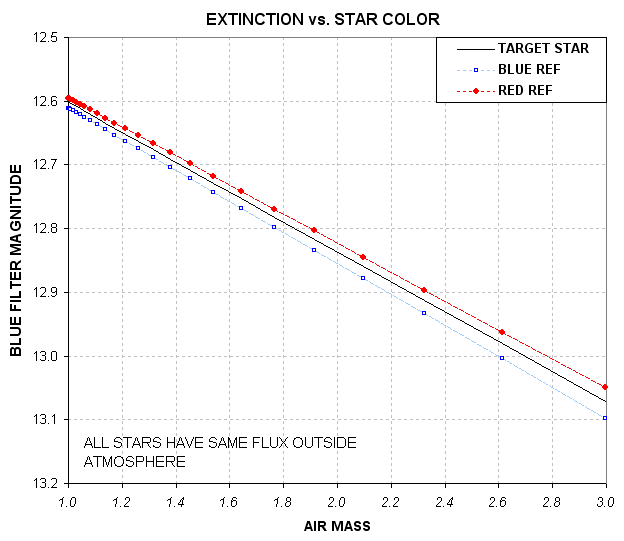
Figure 14.07. Extinction plot for red and blue stars (based on model).

If the target star is cool then the cool reference star should be used. If instead the hot star is used for reference there will be a 32 mmag distortion of the LC that is correlated with airmass. The shape of the LC will be a downward bulge in the middle (at the lowest airmass), as shown in the next figure.

We’ve just shown that when using a B-band filter hot and cool stars can distort LC shapes by the amount ~16 mmag per airmass in opposite directions, producing opposite LC curvatures. What about the other filters? For R-band the two zenith extinctions are 0.120 and 0.123 mag/airmass (for cool and hot stars). The difference is only 3 mmag/airmass, which is much less than for B-band. Nevertheless, a LC bulge of 3 mmag/airmass is important for depths as shallow as 10 to 20 mmag.

Unfiltered observations are more dangerous than filtered ones when choosing reference stars on the basis of color. A cool star has an effective zenith extinction coefficient of 0.132 mag/airmass, unfiltered, versus 0.191 mag/airmass for a hot star. That’s a whopping 59 mmag/airmass! Clearly, attention to star color is more important when observing unfiltered. A much less serious warning applies to observations with a blue-blocking filter (described in greater detail later).

All of the above-cited zenith extinction coefficient dependencies on star color are for a site at 4660 feet. Lower altitude sites will experience greater effects.

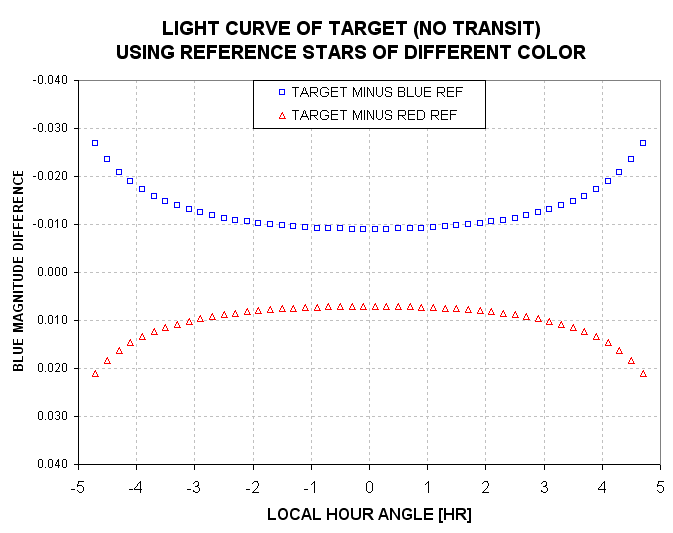
Figure 14.08. Light curve shapes of normal-color star when blue and red reference stars are used and observations are made with a B-band filter.

Is there any evidence for this effect in real data? Yes. Consider the following figure, Fig. 14.09, showing the effect of reference star color on measured LCs.

The middle panel uses a reference star having the same color as the target star. The top panel shows what happens when a red reference star is used. It is bowed upward in the middle. Air mass was minimum at 5.5 UT, which accounts for a greater downward distortion of the LC at the end (when airmass = 1.3, compared when airmass = 1.2 at the beginning). The bottom panel, using slightly bluer stars for reference, has an opposite curvature. The curvature is less pronounced in this panel compared to the middle one due to a smaller color difference.

Notice also in this figure that reference star color not only affects transit shape, it also affects transit depth. Assuming the middle panel is “correct” we can say that the red star (top panel) produced an 10% increase in apparent depth, whereas the blue star (bottom panel) produced a 8% decrease.

One additional effect to note when using a different color reference star is “timing” – by which I mean the time of mid-transit as defined by the average of the times for ingress and egress. For this example the red reference star produced a -2.4-minute error while the blue reference star produced a +2.1-minute error.

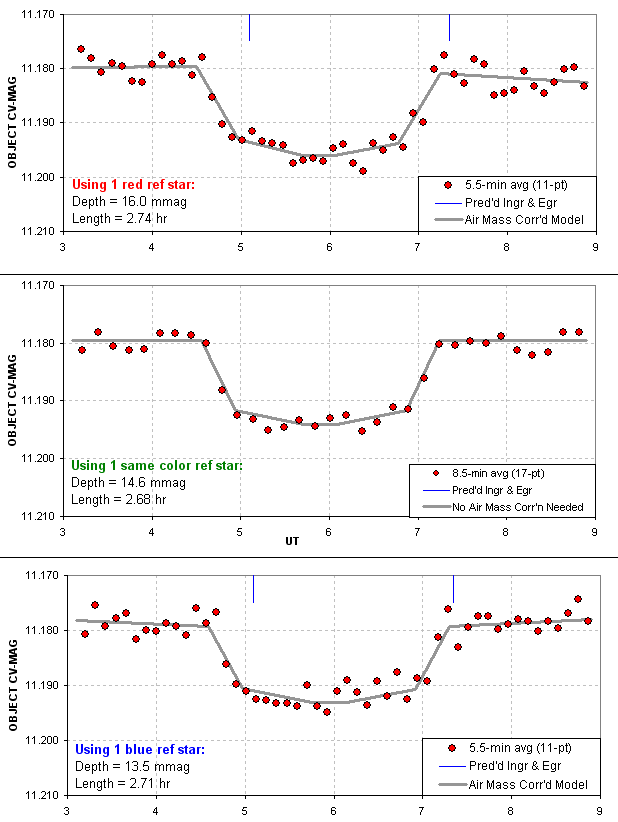
Figure 14.09. Effect of reference star color on LC shape, depth, length and timing.

For shallow transits it is therefore preferable to use a reference star with a color similar to the target star. If this can’t be done then an air mass model may have to be used to interpret the LC. The longer the out-of-transit (OOT) baseline the easier it is to derive a proper fitting model. With experience, and familiarity with the color of stars near the target, it is possible to process the OOT baselines to reduce curvature effects. But when there is uncertainty in star colors it is prudent to plan on a long observing session. Even when a reasonable “fit” is achieved using different color reference stars be prepared for errors in transit depth and timing.

Blue-Blocking Filter

Some observing situations are best approached using a “blue-blocking filter.” As the next graph shows it blocks everything blueward of V-band.

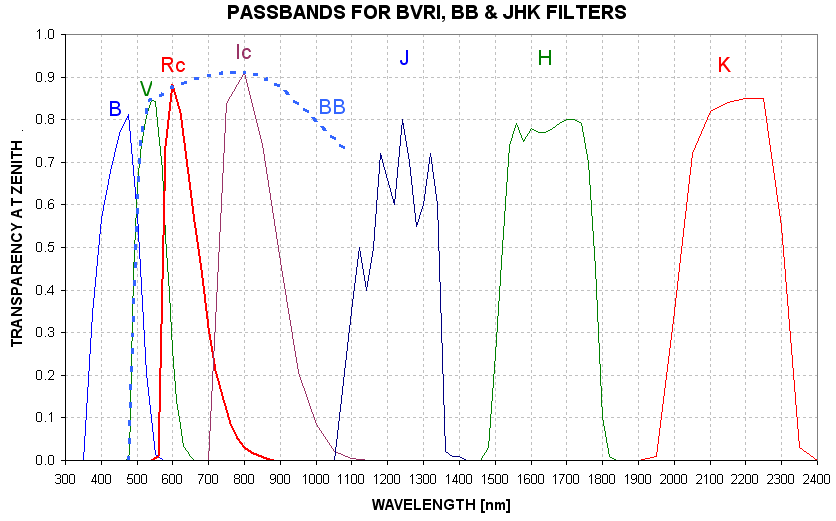
Figure 14.10. Filter response functions times atmospheric transparency for standard B, V, Rc, Ic filters, as well as the 2MASS J, H and K filters. Also shown is the blue-blocking (BB) filter response. Actual response functions will depend on the CCD response.

The BB-filter is attractive for two reasons: 1) it reduces a significant amount of sky background light whenever the moon is above the horizon, and 2) it reduces extinction effects by a large amount without a significant SNR penalty. Concerning the first point, the night sky brightness spectrum will be similar to the site’s extinction spectrum during moon-lit nights. (On moonless nights there’s no reduction of sky background level from use of a BB-filter.) For these reasons at least one wide-field survey camera project uses a BB-filter (Ohio State University’s KELT Project, based at the Winer Observatory, AZ).

When a typical CCD response function is used (my ST-8XE), and adopting my site altitude, the BB-filter’s “white star” effective wavelength is calculated to be 700 nm. This is intermediate between the R-band and I-band filters.

Using a BB-filter stars that are blue and red have calculated extinctions of 0.124 and 0.116 mag/airmass. If a set of images that contain red and blue stars within the FOV were measured and plotted versus air mass they would exhibit these two slopes, i.e., they would separate at the rate of 8 mmag/airmass.

The following list summarizes the calculated extinction slope differences for various filters between stars that are blue (spectral type A2, 8000 K) and red (K3, 4500 K).

B-band 16 mmag/airmass

V-band ~6 mmag/airmass

R-band 3 mmag/airmass

I-band ~1 mmag/airmass

Unfiltered 59 mmag/airmass

BB-band 8 mmag/airmass

The BB-filter offers a dramatic 7-fold reduction of extinction effects compared with using a clear filter (essentially equivalent to unfiltered)! Keep in mind that the red and blue stars used for these calculations are near the extremes of blueness and redness, so the values in the above list are close to the maximum that will be encountered.

The BB-filter’s loss of SNR, compared to using a clear filter, will depend on star color. For a blue star the BB-filter delivers 89% of the counts delivered by a clear filter (at zenith). For a red star it is 94%. The corresponding increases in observing time to achieve the same SNR are 41% and 13%. However, SNR also depends on sky background level, and the BB and clear filters respond differently to changes in sky background. During full moon the sky background is highest, being ~3 magnitudes brighter than on a moonless dark night (away from city lights). Also during full moon Rayleigh scattering of moonlight produces a blue-colored sky background. I haven’t studied this yet but I suspect that whenever the moon is in the sky the BB-filter’s lower sky background level is more important than the few percent loss of signal, leading to an improved SNR instead of a degraded one. In any case, a slight loss of SNR is worth extra observing time in order to achieve dramatic reductions of systematic errors in light curve baseline curvature that would have to be dealt with for unfiltered observations.

Getting Star Colors

The 2MASS (2-Micron All-Sky Survey) star catalog contains ½ billion entries. It is about 99% complete to magnitudes corresponding to V-mag ~17.5. TheSky/Six includes J, H and K magnitudes for almost every star in their maps. The latest version of MPO Canopus (with PhotoRed built-in) makes use of J and K magnitudes to calculate B, V, Rc and Ic magnitudes. J-K star colors are correlated with the more traditional star colors, B-V and V-R, as shown by Caldwell et al (1993), Warner and Harris (2007) and others. The strong correlation breaks down outside the J-K range of -0.1 to 1.0, but within this wavelength region it is possible to predict V-R star colors with an accuracy of 0.021 magnitude (Warner and Harris, 2007). This is adequate for selecting same color reference stars.

Occasionally J and K magnitudes are missing from the star map programs in common use by amateurs (these programs are also referred to by the unfortunate name “planetarium programs”). When you need J-K for only a few such stars the following web site is useful: http://irsa.ipac.caltech.edu/

Converting between J-K and B-V can be done using the following equivalence (based on a scatter plot published by Warner and Harris, 2007):

B-V = +0.07 + 1.489 (J-K) or J-K = -0.15 + 0.672 (B-V)

In choosing same-color reference stars be careful to not use any with J-K > 1.0, where J-K to B-V and V-R correlations can be double-valued. Staying within this color range corresponds to -0.1 < B-V < 1.5. For stars meeting this criterion the median B-V is +0.65, based on a histogram of 1259 Landolt star B-V values.

Figure 14.11. Histogram of B-V for 1259 Landolt stars.

This histogram shows that the bluest 25% of stars have B-V < +0.47. Using the Warner and Harris equation this corresponds to J-K < +0.26. The reddest 25% of stars with acceptable colors have B-V > +1.01, which corresponds to J-K > +0.64. If there were 12 candidate reference stars in a FOV, for example, it is likely there would be 3 with J-K < +0.26 and another 3 with J-K > +0.64. If the target star is typical, with J-K ~ 0.39, there should be ~6 stars with a J-K color difference less than ~0.2. Therefore:

A reasonable goal for “same color” stars is a J-K difference < ~0.2.

It’s possible to associate J-K with star surface temperature. The typical J-K of +0.4 corresponds to Tstar = 5800 K. The bluest 25% of stars have Tstar > ~7700 K, and the reddest 25% have Tstar < ~4000 K. These are close to the temperature extremes that were used to calculate zenith extinction sensitivities to star color. Therefore, the list of extinction slope differences for red and blue stars, for various filters (in the previous section of this chapter), should be representative of situations faced by exoplanet transit observers. In other words,…

Star color matters!

─────────────────────────────────

Chapter 15

Stochastic Error Budget

─────────────────────────────────

This chapter will illustrate how stochastic noise contributes to the “scatter” of points in a light curve. I will treat the following error sources: Poisson noise, aperture pixel noise, scintillation noise and seeing noise. All of these components can be treated as stochastic noise. Poisson and scintillation noise are usually the most important components. I will assume that several stars are chosen for use as reference (“ensemble photometry”).

“Stochastic” uncertainty is produced by a category of fluctuation related to random events. For example, it is believed that the clicking of a Geiger counter is random because the ejection of a nuclear particle is unrelated to events in the larger world; such events are instead prompted by laws that are not yet understood governing events within the nucleus. To observers in the outer world the particle ejections of radioactive nuclei occur at random times.

Photons from the heavens arrive at a CCD and release an electron (called a “photoelectron”) at times that can also be treated as random. As a practical matter, the noise generated by thermal agitation within the CCD and nearby circuitry is also a random process. Scintillation is generated at the tropopause and causes destructive and constructive interference of wave fronts at the CCD, causing the rate of photon flux at the detector to fluctuate in what appears to be a random manner. All of these processes exhibit an underlying randomness, and their impact on measurements is referred to as “stochastic noise.” The “Poisson process” is a mathematical treatment of the probabilities of the occurrence of discrete random events that produce stochastic noise.

The previous chapters dealt with “systematic uncertainties” and tried to identify which ones were most important. This chapter deals with sources of stochastic uncertainty in an effort to identify which ones are most important. Both sources of uncertainty are important aspects of any measurement, and I’m a proponent of the following:

“A measurement is not a measurement until it has been assigned stochastic and systematic uncertainties.”

This may be an extreme position, but it highlights the importance of understanding both categories of uncertainty that are associated with EVERY measurement, in every field of science. This chapter therefore strives to give balance to the book by describing the other half of uncertainties in photometry. The components of stochastic noise will be treated using the XO-3 star field as an example, with specific reference to my 2007.04.15 observations of it.

Poisson Noise

A Poisson distribution describes what can be expected when a finite number of “random” events produce a measured "count" (an integer) during a pre-set time interval. This is the situation for readings of each CCD pixel at the end of an exposure. Consider the process of a photon dislodging an electron from a silicon crystal in the CCD (related to the "photoelectric effect"). This one event yields one electron for detection after the exposure is complete. When a pixel is "read" by electronic circuitry this one electron will contribute to that pixel’s ADU count by an amount that depends on the CCD gain. For my SBIG ST-8E CCD, the gain is 2.3 electrons per count (where each "count" is also called an ADU, or analog data unit). Therefore, the number of photoelectrons needed to produce a count of C is n = 2.3×C (for my CCD). This is true whether I define C to be the count from just one pixel or the sum of counts produced by a star that may be registered by several pixels (called flux). You can measure your CCD’s gain and it may differ significantly from the value given in the User’s Manual. For example, my CCD has a gain of ~2.7 instead of 2.3 electrons per ADU.

Stochastic events have the property that the SE uncertainty of the total number of events is the square-root of the number of such events (provided the number of events is large). Thus, when we measure n stochastic events occurring within a specified integration interval, we must state that we have really just measured a value n ± sqrt(n) events. Since the measurement C is based on 2.3×C events (for this particular CCD) we must state that we have measured: 2.3×C ± sqrt (2.3×C) "events." Stated in terms of counts, we measure C ± sqrt (C/2.3). This fundamental uncertainty is referred to as Poisson noise. To summarize, Poisson noise from a bright star is:

Np = sqrt (C / gain)

Np = sqrt (C / 2.3) for the SBIG ST-8E CCD.

This result can be expressed in terms of mmag:

Poisson SE [mmag] = 1086 / sqrt (2.3×C )

Whenever an exoplanet’s light curve is to be produced from a set of images there will usually be several stars suitable for use as reference stars. Consider the example of XO-3, whose star field is presented in the figure on the next page. Note that XO-3 has a B-V color of 0.45, whereas all other stars are redder (larger values of B-V). Only two stars have close to the same color, stars #1 and #6. In the following example these two stars will be used for ensemble photometry reference.

On the date 2007.04.15 this star field was observed with an I-band filter, with exposure times of 60 seconds, binned 1x1 and CCD cooler set to -24 ˚C (with my 14-inch telescope). FWHM was typically 6 pixels, so I chose a signal aperture photometry radius of 15 pixels (2.5 × FWHM, a safe choice). With this aperture the measured fluxes for XO-3, Star #1 and Star #6 were 346000, 161000 and 963000 counts. The maximum counts for these stars varied with FWHM, of course, but typically they were ~9200, 4300 and 22000 counts (SNR ~3000, 1100 and 8000.) Using the above equation we calculate Np values for the three stars to be 388, 265 and 647 counts. Measurements of each star will have Poisson uncertainties of 1.22, 1.78 and 0.73 mmag (i.e., 1086 / sqrt (2.3 × Flux). For each image the three flux readings will be converted to magnitudes and the XO-3 magnitude will be adjusted by whatever amount is needed to bring the average magnitude of the two reference stars into agreement with what is expected for them from an atmospheric model for extinction.

Figure 15.01. XO-3 star field, showing BVRcIc colors of several stars. The B-V star colors are shown in large blue numbers.

Using the above example, the ensemble photometry adjustment will have an uncertainty given by ½ × (1.78² + 0.73²)^0.5 = 0.96 mmag. The general equation for this (homework for the reader) is:

Ensemble Photometry Poisson SE = 1/n × (SE₁² + SE₂² + SE₃² + … +SE_n²)^½

where n is the number of reference stars and SE_n are the Poisson uncertainties for each reference star (expressed in mmag units). Clearly, as n increases the effect of uncertainties (due to Poisson noise) diminishes, approaching the limit zero for an infinite number of reference stars. XO-3’s Poisson noise uncertainty of 1.22 mmag must be orthogonally added to the Poisson uncertainty produced by the reference stars. Hence, after performing an ensemble photometry adjustment using these two reference stars XO-3 will exhibit a total Poisson noise uncertainty of (1.22² + 0.96²)^½= 1.55 mmag. This is the Poisson component of RMS scatter for each image that can be expected in a final light curve.

Aperture Pixel Noise

Consider noise contributions from the process of "reading" the CCD ("CCD read noise"), plus noise produced by thermal agitation of the crystal's atoms ("CCD dark current noise"), and finally from noise produced by a sky that is not totally dark ("sky background noise"). These are three additional sources of noise in each CCD reading (the last two are Poisson themselves since they are based on discrete stochastic events, but we’ll treat them here in the traditional manner). These three noise sources are small when the star in the photometry aperture is bright and the CCD is very cold (to reduce dark current noise). For that situation it can be stated that the star's measured flux (total counts within the aperture minus an expected background level) will be uncertain by an amount given in the previous section. If, however, the CCD is not very cold (which is going to be the case for amateurs without LN2 cooling), and when the sky is bright (too often the case for amateur observing sites), these components of noise cannot be ignored.

I’ll use the term “aperture pixel noise” to refer to the sum of these three sources of noise (sky background level, CCD dark current noise, and CCD readout noise). When the photometry aperture is moved to a location where there are no stars MaxIm DL (MDL) displays the RMS scatter for both the signal aperture and sky background annulus. For the 2007.04.15 observations this RMS was ~4.3 counts. The fact that each pixel’s reading has a finite uncertainty has two effects: 1) the average level for the sky annulus background is not perfectly established, and 2) the flux within the aperture (the sum of differences between the signal aperture pixel readings and the average background level) is also uncertain.

Among the b pixels within the sky background annulus the average count is Cb and the standard deviation of these counts is Ni, which we will identify as the source for “aperture pixel noise.” We will assume that every pixel in the image has a stochastic uncertainty of Ni. The average value for the sky background level has an uncertainty given by Nb = Ni / sqrt (b-1).

Star flux is defined to be the sum of counts above a background level. One way to view this calculation is to subtract the background level from each signal aperture pixel count, and then perform a summation. An equivalent view is to sum the signal aperture counts, then subtract the sum of an equal number of background levels. The second way of viewing the calculation lends itself to a simple way of calculating SE on the calculated flux, since we’re simply subtracting one value from another and each value has its own uncertainty. The first value, the sum of signal aperture counts, will be uncertain by the amount Nss = Ni × sqrt (s), where s is the number of pixels within the signal aperture. The second number, the sum of counts that would be expected for these s pixels if no star were present within the signal aperture, will have an uncertainty Nbs = Nb × sqrt (s) = sqrt (s) × Ni / sqrt (b). The uncertainty on calculated star flux (neglecting Poisson noise) will be the orthogonal sum of these two uncertainties. In other words, since Ns² = Nss² + Nbs², we derive that Ns² = s × Ni² × (1 + 1/b), and since (1 + 1/b) ~ 1, we can state that:

Ns= sqrt(s) × Ni.

Since the 2007.04.15 images exhibit Ni ~ 4.3 counts, and since s = π 15²= 707 pixels, we calculate that Ns = 114 counts. For XO-3, producing 346000 counts, this represents an uncertainty of 0.36 mmag. Notice that this is less than Poisson noise.

Scintillation Noise

At tropopause altitudes clear air turbulence is common, and the temperature inhomogeneities produced by turbulence cause slight bending of the wave fronts of starlight which produce a component of constructive and destructive interference at ground level, which we observe as scintillation. The smaller the aperture, the greater the scintillation. The naked eye’s aperture is so small that an additional component of scintillation is produced by temperature and humidity inhomogeneities near ground level (where “atmospheric seeing” degradation is produced). These visual changes in brightness are called "twinkling" and because the tropopause component is common to both there is a correlation between the amount of twinkling and scintillation. Incidentally, since atmospheric seeing is degraded mostly by turbulence near the ground, visually perceived twinkling and seeing are partially correlated whereas scintillation and seeing are less correlated.

Everyone knows that stars “twinkle” different amounts on different nights. Twinkling also is greater near the horizon. Faint stars twinkle as much as bright stars. Planets don't twinkle. What’s going on?

These common facts are helpful in understanding what to expect for attempts to monitor the brightness of a star that is undergoing an exoplanet transit. For example, the fact that planets don't twinkle means that a reference star's scintillation (another word for twinkling) will be uncorrelated with the target star's scintillation (since the angular separation of reference and target stars is greater than the angular size of a planet, and planets don’t twinkle). This is unfortunate, for it means that a differential photometry analysis that uses one reference star will increase the target star's brightness variations due to scintillation by ~41% (i.e., the fluctuations are root-2 times the value without using a reference star). Using many reference stars reduces the effect of uncorrelated reference star scintillation back to where it is dominated by just the target star's scintillation. It also can be stated that there's no need to choose reference stars that are near the target star to reduce scintillation, since essentially all correlation is lost beyond angular distances of ~10 "arc (a typical planet angular diameter).

A classic study of scintillation was published by Dravins et al (1998). They studied scintillation’s dependence upon telescope aperture, air mass, site altitude and exposure time. Their equation relating all these parameters is:

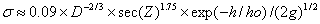
where σ = fractional intensity RMS fluctuation (scintillation), D = telescope diameter [cm], sec(Z) = air mass, h = observatory site altitude above sea level [m], h₀ (atmospheric scale height) = 8000 [m], and g = exposure time [sec].

For me, h = 1420 meters and D = 35.6 cm, so I calculate an expected typical scintillation noise to be:

Scintillation noise [mmag] = 5.35 × AirMass^1.75 / sqrt(g)

where g = exposure time [seconds]. For air mass = 1.9 and T = 60 seconds, scintillation = 2.12 mmag. Keep in mind that the magnitude of scintillation may vary greatly from night-to-night, as well as on time scales of a few minutes.

Seeing Noise

When I made about 1000 short exposures of the moon for the purpose of creating an animation showing terminator movement I encountered two unexpected things: 1) seeing varied across each image, and 2) position distortions were present. The first item means that no single image was sharp at all parts of the image. One image might be sharp in the upper-left hand area (FWHM ~1.5 ”arc) and fuzzy elsewhere (3.5 ”arc), while the next image might be sharp in the middle only. My impression is that the sharpness auto-correlation function usually went to zero ~5 ’arc away, and the areas where one image was sharp were poorly correlated with the next image’s sharp areas. The second item means that position distortions within an image were present, which made it impossible to combine two images with just one offset for bringing all regions of the FOV into alignment. A time-lapse movie of these images resembles looking into a swimming pool and seeing different parts of the pool bottom move in ways that were uncorrelated. These two phenomena were seen for about two hours, so it wasn’t just an early evening atmospheric effect. I used a V-band filter, an exposure time of 0.1 second and images were spaced ~8 seconds apart. (Some of these moon images can be seen at http://brucegary.net/Moon/Moon7524.htm and an animation of seeing can be found at http://brucegary.net/ASD/x.htm, Fig. 4.)

Since these were short exposures the spatial seeing differences were entirely atmospheric, unlike long exposures that can be influenced by imperfect tracking. Even with perfect tracking we can predict that the longer the exposure the smaller the spatial differences in sharpness. To understand this, imagine a 3-dimensional field of atmospheric temperature with inhomogeneities that are “frozen” with respect to the air. Now imagine that the air is moving and carrying the temperature structure across the telescope’s line-of-sight. At one instant the line-of-sight to one part of the FOV may be relatively free of temperature structure, and exhibit sharpness, while the opposite is true for another line-of-sight. But as the air moves past the telescope the regions of sharpness in the FOV will vary. If a typical time for variation is 1 second, for example, then after 16 seconds the contrast in sharpness will be of order 1/4^th as large compared with the contrast for individual short exposures. In theory, there will always be some variation of FWHM sharpness across an image, regardless of exposure time.

Consider using an aperture that captures a fraction of the complete PSF for a star. Refer to Fig. 10.02 for a plot of photometry signal aperture “capture fraction” versus size of the aperture in relation to FWHM. For a typical choice of aperture radius ~2.5 times FWHM, 99% of a star’s total flux is captured by the photometry aperture. If FHWM varies across the image within the range 3.0 to 3.3 ”arc, for example, the capture fraction could vary between 0.987 and 0.980, or 7.6 mmag. Smaller apertures would produce even larger differences.

Since patterns of seeing across an image will be uncorrelated from one image to the next (if they have exposure times longer than ~10 seconds), the errors in relating an exoplanet’s flux to the fluxes of references stars (produced by seeing variations) will be different from image to image. The effect of this upon a light curve is to merely increase RMS scatter. In other words, there won’t be any systematic effects that would change the shape of the light curve. This is my reason for including variable seeing in this chapter as “noise.”

I don’t know of any study analogous to that by Dravin’s et al (1993) that can be used to predict the magnitude of noise introduced to a light curve by seeing variations. For the moment let’s simply treat it as an unknown small effect, and if empirically-determined RMS scatter requires invoking something unknown we can consider seeing variations to be a candidate for explanation.

Comparing Observed with Predicted RMS Scatter

For the 2007.04.15 observations I measured an RMS scatter of 2.63 mmag for a one-hour period. How does this compare with the total errors calculated in the previous sections? Here’s the list:

1.55 mmag Poisson noise

0.36 mmag Aperture pixel noise

~2.12 mmag Scintillation noise

?.?? mmag Unidentified sources of noise (“seeing” noise, etc.)

~2.65 mmag Total noise predicted

2.63 mmag Measured noise

The agreement is acceptable, especially considering the uncertainties. The most variable of these components is scintillation noise. The amplitude of scintillation can change by a factor two during the course of minutes, and night to night variations can differ by similar amounts (depending on the location of jet stream winds).

It’s possible to evaluate the presence of “seeing noise” by reprocessing images using a large photometry aperture. For example, when the 2007.04.15 images are processed using an aperture radius of 20 pixels instead of 15, the measured RMS scatter increases to 2.76 mmag. Some increase can be expected from a larger “aperture pixel noise” (the predicted total noise changes from 2.65 to 2.67 mmag), but the fact that the measured noise increased more than the predicted amount, instead of decreasing, suggests that “seeing noise” was not important for this observing session.

I use a special spreadsheet to help guide the choice of reference stars. It allows me to see the predicted effect of adopting various sets of reference stars and aperture sizes. For example, notice in Fig. 15.01 that Star #4 is much brighter than the other stars that I adopted for use as reference. If it replaced Star #1 the RMS scatter is predicted to be reduced to 2.50 mmag. This is a small payoff considering the extreme redness of Star #4, which can be verified in the photometry analysis spreadsheet by actually trying out the use of Star #4 instead of Star #1 for reference.

It should be noted here that the case of 2007.04.15, based on use of an I-band filter, is not meant to show a representative RMS scatter for light curves. Lower scatter can be achieved by observing with an R-band filter (1.7 times as much flux), or a blue-blocking BB-band filter (4 times the flux). Also, the XO-3 star field does not have a good choice for same color stars, and this affects the level of RMS scatter that can be achieved. XO-1 and XO-2, for example, provide better reference star candidates. It is possible to achieve ~1 mmag RMS scatter per 1-minute image using a 14-inch telescope provided a good set of reference stars is nearby, a R-band or BB-band filter is used, and scintillation conditions are low.

Larger telescope apertures should be able to achieve lower “mmag precision” in spite of the fact that exposure times would have to be shortened to avoid saturation. It should be each observer's responsibility to use the concepts described here to calculate an observing strategy that produces light curves with a minimum RMS scatter as well as a minimum of systematic errors based on the observer’s specific telescope and observatory situation.

An excellent discussion of CCD hardware can be found in the book Handbook of CCD Astronomy (2000) by Steve B. Howell. Some of the material in this chapter is based on this book.

─────────────────────────────────

Chapter 16

Anomalies: Timing and LC Shape

─────────────────────────────────

Timing Anomalies and Other Exoplanets

A transiting hot Jupiter exoplanet in a circular orbit with no other planets in the system will produce transits at uniformly spaced intervals. This statement neglects the very slow third-order effect related to the star’s oblateness, but these changes are very slow. If the hot Jupiter is in an elliptical orbit the transits will shift steadily in time due to precession of the orbit’s periastron (location of closest approach to the star). In that case the transits may also change shape, or entirely disappear (though unlikely in a lifetime).

A more interesting possibility is for the hot Jupiter to exhibit anomalies that change over the course of a few months due to another planet in an orbit close to that of the hot Jupiter (Algol et al, 2005; Holman and Murray, 2005, Steffen, 2006). The greatest effects will be produced when the orbit periods are resonant. For example, if an Earth-like planet is in a 2:1 period resonance with the hot Jupiter, it can cause the hot Jupiter to shift its orbital position in ways that cause transits to alternate between coming early or late with a periodicity on the order of a year. The amplitude of these “timing anomalies” can be as high as 3 minutes (Steffen, 2006).

This is perhaps the most exciting aspect of amateur participation in exoplanet transit observing. Ground-based professional telescopes are too expensive, on a per minute basis, for such long term projects. Space-based telescopes devoted to such a project could do a good job with this, but so far the ones in orbit, or scheduled to launch, are designed for specific tasks that render them unsuited or unable to conduct the required follow-up observations of all transiting exoplanets. For example, the Kepler Mission telescope will stare at the same star field (Lyra/Cyngus) for 4 to 6 years. It will therefore not be used to search for Earth-sized planets in the known transiting exoplanet systems. Within a few years there could be several dozen transiting exoplanets, and probably all of them will be outside the Kepler Telescope’s FOV. Thus, ground-based and other space-based telescopes will be needed for transit timing variability studies.

Any transit observation meant to contribute to an archive of mid-transit timings should be made with careful attention to accurate image time-tags. This means the computer that records images should use a program that automatically synchronizes the computer’s clock with a time standard. I use AtomTimePro, which I’ve set for updates every 3 hours. The user should also pay attention to the “meaning” of image time tags. For example, MaxIm DL records start times in the FITS header, but when it performs photometry the CSV-file has a JD value corresponding to the mid-exposure time.

Amateur timings are likely to exhibit uncertainties of 1 or 2 minutes for each transit’s mid-transit time. This is based on my analysis of XO-1 amateur timing measurements. Averaging of many timing measurements will reduce this uncertainty.

The next graph is a plot of 28 XO-1 transit timings by mostly amateurs during the period 2004 to 2007. There is nothing unusual about the pattern of timings in relation to a straight line fit. This corresponds to a constant period. So far, however, all observations are clustered near “opposition” at yearly intervals, so a one-year periodicity cannot be ruled out. Other periodicities appear to be constrained to amplitudes less than ~0.001 day, or 1.4-minutes.

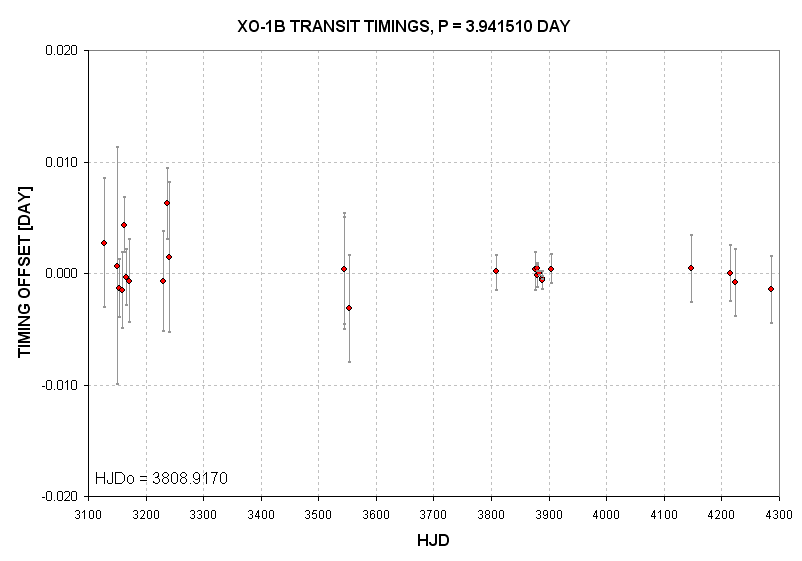
Figure 16.01. Transit timings for XO-1.

This is just one example of what amateurs are capable of doing in a search for timing anomalies. As more amateurs join the ranks of exoplanet transit observers there will be a more data dense archive of timings to work with for this and the other exoplanets.

Light Curve Shape Anomalies

Jupiter and Saturn both have rings and moons, so it is reasonable to wonder if hot Jupiter exoplanets also have them. Specifically, can amateurs detect their presence from high quality light curves.

Shortly after TrES-1 was announced (in 2004) a group of amateurs observed transits of this exoplanet and shared their light curves. I saw evidence of a brightening right before ingress and possibly right after egress in several of these light curves. Joe Garlitz in Oregon also noticed this unusual feature. Someone called my attention to studies by Barnes and Fortney (2003) who had investigated the possibility of detecting the presence of rings around giant exoplanets by searching for light curve brightening just outside transit that would be produced by forward scattering of star light. Ron Bissinger performed a detailed analysis of light curve observations (mostly amateur) and concluded that the brightenings were statistically significant but required confirmation (Bissinger, 2005). The Hubble Space Telescope later failed to confirm these brightenings. Nevertheless, each new transiting exoplanet discovery represents another possibility for detecting exoplanet rings.

Another light curve anomaly to look for is an extra loss of brightness just before ingress, or just after egress, caused by a large moon of the exoplanet responsible for the main transit event. Searches have so far failed to detect the expected feature of an exoplanet moon, but the value of such a discovery means that every new exoplanet discovered should be studied with this feature in mind.

Rings and moons will produce brightening and fading anomalies that are much smaller than the main transit event’s mid-transit depth. The Hubble Space Telescope is ideal for this task. However, HST will eventually degrade and become unusable, and this may happen before the James Webb Space Telescope is launched (2013 or later). Amateurs wishing to beat the big space-based telescopes in detecting rings or moons should consider performing a median combine of many ingress and egress observations. Rings are likely to be present for both ingress and egress, so folding of egress to match the shape of ingress is permissible. Moons are likely to be in an orbit that resonates with the exoplanet’s orbit about the star, which means that if one ingress shows a fade feature other ingress events are also likely to show the same fade feature. This means that there probably is reason to stack ingresses, and also stack egresses. But don’t fold egress data with ingress because a moon is not likely to affect both. Data averaging is advisable. I recommend 5-minute bins. However, “running averages” are unsafe at any size and should be avoided because they easily produce the impression of self-consistent patterns that don’t exist.

Small amplitude oscillations within a transit are sometimes thought to exist in measurements, but it is prudent to assume that at this time none of them are real. Still, small features within a transit are worth searching for. After all, the star undergoing transit may have sunspots. A credible detection of such a feature would require confirmation from simultaneous observations by another observer. Observer teams may some day coordinate observations of the same transit for this purpose.

Don’t forget that it is always worth observing a transiting exoplanet between transits in a search for anomalous fades caused by another exoplanet in the same star system. The length of such a fade event could be shorter than the main transit length (if the new planet is in an inner orbit) or longer (if in an outer orbit).

Other subtle anomalies of exoplanet light curves may become important as theoreticians and observationalists continue the study of this new field. Every observer should therefore be prepared to accept as “real” an observational anomaly that is not readily explained. Part of the excitement of exoplanet observing is that this is a young field that may produce future surprises not yet imagined.

Since amateurs have a unique opportunity to contribute to timing studies of known exoplanets, and thereby contribute to the discovery of Earth-mass exoplanets, there is a growing need for more advanced exoplanet observers as more exoplanets are discovered. It will be important for these amateurs to coordinate their observations, and to contribute them to a standard format archive. A case will be presented in the next chapter for establishing such an archive. I claim that attention should be paid to what constitutes an “optimum observatory” for exoplanet observing. This is also a topic for the next chapter.

─-───────────────────────────────

Chapter 17

Optimum Observatory

─────────────────────────────────

Dreaming! Every amateur dreams about upgrades to the backyard observatory.

Whenever someone asks for a recommendation of what telescope to buy, I have to first ask “What do you want to do with it?” For “pretty pictures” of a specific category of objects the answer would be one kind of telescope and camera (about which I would be clueless, since I’m no good at that). But for exoplanet transit light curves, I could give a pretty specific answer. That’s what this chapter is about.

Some of the following paragraphs (presented in smaller font) are taken from a “white paper” I submitted to the NASA/NSF “Exoplanet Task Force” (ExoPTF) in March, 2007. My white paper argued for government sponsorship of a network of amateur observatories for coordinated monitoring of known transiting exoplanets for the purpose of discovering Earth-sized exoplanets. Part of the case I presented was that the optimum observatory for this task is only slightly more expensive than existing amateur budgets, yet sufficiently more expensive for those few amateurs who are capable of participating in such a search that financial help is needed. (If you interpret this to be a shameless, self-serving attempt to upgrade my observatory by responding to a future “request for proposal” by NASA, you would be correct!)

Here is the argument I presented to the ExoPTF in which I derived that the optimum observatory would consist of a 20 to 30-inch aperture telescope as part of an observatory costing ~$75,000. (I now realize that the aperture range should be 20 to 40 inches).

Precision photometry (i.e., 1-minute precision of ~2 mmag) has many requirements: 1) the plate scale should assure that a star’s full-width at half-maximum (FWHM) be at least 3 pixels. For CCD cameras using chips having 9 micron pixels, and for sites with FHWM ~ 2.5 “arc, this means the plate scale should be ~0.7 “arc/pixel. If the plate scale is smaller too many pixels are within the photometry aperture circle, leading to SNR degradation. 2) An aperture should be large enough that Poisson noise and scintillation noise are small. 3) The focal length should be short enough that the FOV is likely to contain same-color stars for use as reference; this requirement translates to FOV larger than ~12 x 18 ‘arc. 4) The telescope should be in a mount that does not require meridian flips. 5) Image quality must be the same for the entire FOV; in other words, focal reducers cannot be used. 6) There should be minimal degradation of image sharpness due to winds vibrating the telescope; this translates to either the use of an open tube or a closed tube inside a dome.

The optimum effective focal length (EFL) is ~100 inches when 9 micron pixel dimensions are used and FWHM seeing of ~2.5 “arc is to be accommodated. A 30-inch telescope would have to have an f-ratio of 3.3 to achieve this EFL without using a focal reducer lens. When f-ratio becomes small, maintaining optical collimation becomes more difficult. This is one reason larger apertures are undesirable. A 40-inch aperture with f-ratio = 5 will have EFL = 200 inches, a plate scale of 0.35 “arc/pixel and a FOV =17 x 11 ’arc when a large format CCD is used (35 mm longest dimension). The plate scale is acceptable since the noise penalty of having to use 4 times as many pixels in the signal aperture for a 2.5 “arc FWHM star will be compensated by the larger aperture collecting area. Any larger aperture, however, will reduce the FOV, which will begin to limit the number of stars available for use as reference. Thus, a 40-inch aperture is an approximate upper limit for the range of apertures that are optimum for exoplanet light curve measurements. (XO-2 is a special case, because an identical star is located 31 “arc away.)

To illustrate some considerations in selecting an “exoplanet optimum” telescope system, consider the following specific components. The 20-inch Meade RCX 400 has a tube made with low-thermal expansion material, which would reduce the need for focus adjustments. The optical design is a modified version of Ritchey-Chrétien, and produces sharp images for a large FOV. It has an f-ratio of 8, so the EFL is 160 inches, yielding a plate scale of 0.46 “arc/pixel. The FOV with a large format CCD chip would be 20x30 ‘arc. The German equatorial mount that it normally comes with is unacceptable for exoplanet observing. The Optical Tube Assembly (OTA) alone would cost ~$20k and a quality fork mount purchased separately would cost ~$25k. Integrating the OTA to the fork mount might cost another $5k. Since the RCX telescope is a closed-tube OTA a dome would be needed to protect it from wind vibrations. This will add another ~$15k for an automated dome. A large format CCD would cost ~$10k. SBIG’s AO-L tip/tilt image stabilizer costs $2k. Buried cables for controlling the telescope, CCD and dome, plus a computer system with control software would cost ~$3k. The total cost for this system is ~$80k.

Other options are possible. A ScopeCraft 24-inch, f/3.1, open tube telescope with a roller-driven horseshoe mount would cost ~$45k. A dome would not be needed for such a telescope, but a sliding roof observatory would be, costing ~$10k. The same CCD camera and other items would be needed, so the total cost would be about the same, or ~$70k.

Most hot Jupiter exoplanet transits last ~3 hours. Because of the need for verifying that reference star color is not affecting the transit shape, depth and mid-transit timing (in a manner that is correlated with air mass), it is important to start observations at least 1.5 hours before ingress and continue until at least 1.5 hours after egress. Thus, 6-hour observing sessions are common, and 8-hour sessions are even better. Observations for more than one observing site are sometimes needed, provided the sites span a sufficient longitude. When observations from two or more observatories are to be combined to produce one light curve, it is helpful that they be identical systems. Systematic effects can be minimized when using the same image scale (same blending of interfering stars), same FOV (allowing for use of the same reference stars) and the same image quality (use of the same photometry apertures).

From there in the white paper I went on to argue that a network of these optimum observatories should be constructed at sites spanning a wide longitude range to assure that each transit would be observed in its entirety. It is clear that such an amateur project would be cheaper than any space-based telescope mission, or any network of professional ground-based observatories.

I envision a network of 6 identical telescopes deployed in the backyards of amateur exoplanet observers who have a demonstrated history of quality observing and dedication to the task. A range of longitudes would be needed to provide coverage of entire transits. The observatories should consist of pairs, with a pair at each of three longitudes. Pair members should be at sufficient distance from each other to reduce the chances that bad weather at one location is correlated with bad weather at the other location. A more important reason for situating identical observatories in same longitude pairs is to provide redundant observations that could support each other when a real LC anomalous feature occurs. This is similar to the principle aspired to by SETI projects in which two telescopes observe the same candidate stars in coordination; if an unusual signal is detected by one telescope the other one, located sufficiently far away to not be affected by the same local interferences, can provide corroboration (not yet implemented).

A network of advanced amateur observatories optimized for exoplanet transit observing should have the guidance of a professional astronomer. He will know other professionals to contact when unexpected observed behaviors are encountered. Once the initial construction costs have been borne the part-time professional will probably constitute the major cost for continued operation of the exoplanet observing network.

At the present time there is no “universal archive” for exoplanet timings or light curve measurements. Each group of observers maintains their own archive, but these groups do not share because of an understandable desire to announce discoveries and continue to be funded by their sponsoring agency. However, a greater good will eventually be served by creating a global archive, fashioned along the lines of the AAVSO (American Association of Variable Star Observers). Even non-members of the AAVSO can submit observations to their immense archive of star brightness observations, and submit queries for what’s in the archive for a specific star for a specific date interval.

I am suggesting the creation of an Exoplanet Transit Archive (ETA) that would maintain light curve observations as well as mid-transit timing submissions. It would be possible for the ETA to perform automated analyses of submitted LC data to solve for air mass curvature and temporal trends, then solve for transit shape using a simple model. The output of this analysis would be a refined set of values for mid-transit time, transit depth, transit length, a shape parameter (related to the ratio of planet radius to star radius). ETA should be available to anyone, both for data submission and information query. The need for ETA will grow with the number of exoplanet observers. The ETA staff should be familiar with common shortcomings of amateur exoplanet transit observations in order to maximize the value of extracted information and minimize the amount of misleading information from ETA submissions. Since the proposed network of amateur observatories described in this chapter is in response to the growing need for amateur observations, and since the proposed network of advanced amateur observers will be familiar with exoplanet observing pitfalls, it is natural for the ETA to be created in coordination with the amateur observatory network. The professional astronomer chosen to lead the amateur network of advanced observers should therefore be charged with creating the ETA.

I believe this is the best time for either government or institutional funding for creating such a professional/amateur partnership. If 2007 is eventually viewed as the year transiting exoplanet discoveries began to “explode,” how fitting if it were also the year that a commitment was made to creating the ETA and a network of identical amateur observatories. This first decade of the 21^st Century has the potential for becoming one of the most exciting periods in the history of astronomy, especially for the amateur astronomer.

APPENDIX A – Evaluating Flat Field Quality

Chapter 5 described a way to create a master flat field. This appendix describes ways to evaluate the quality of a flat field. Recall the two sets of flat fields in Chapter 5 made with different optical configurations, repeated here.

Figure A.01 Flats for B, V, Rc and Ic filters for a configuration with a focal reducer lens placed far from the CCD chip The edge responses are ~63% of the center.

Figure A.02 Flats using the same filters but with a configuration with the same focal reducer close to the CCD chip. The response range, smallest response to maximum, are 88, 90, 89 and 89% for the B, V, Rc and Ic filters.

The first set of flats is relatively featureless aside from the overall pattern of a fall off toward the edge, which resembles classical vignetting. The second set shows more structure, including two dust donuts. Before we condemn the second set of flats as a bad configuration for transit systematics recall that what matters is the change of “flat field error” versus pixel location. There’s no straight-forward way of knowing “flat field error” versus FOV location for a given filter and a specified star color. In fact, each star must have an appropriate flat field for its color. For observations with a V-band filter what will a red star’s optimum flat field look like? It probably will be a blend of the V-band and R-band flat fields. Notice how different the V-band and R-band flat fields are in Fig. A.02. A blue star, on the other hand, may need to be corrected using a blend of the B-band and V-band flat fields.

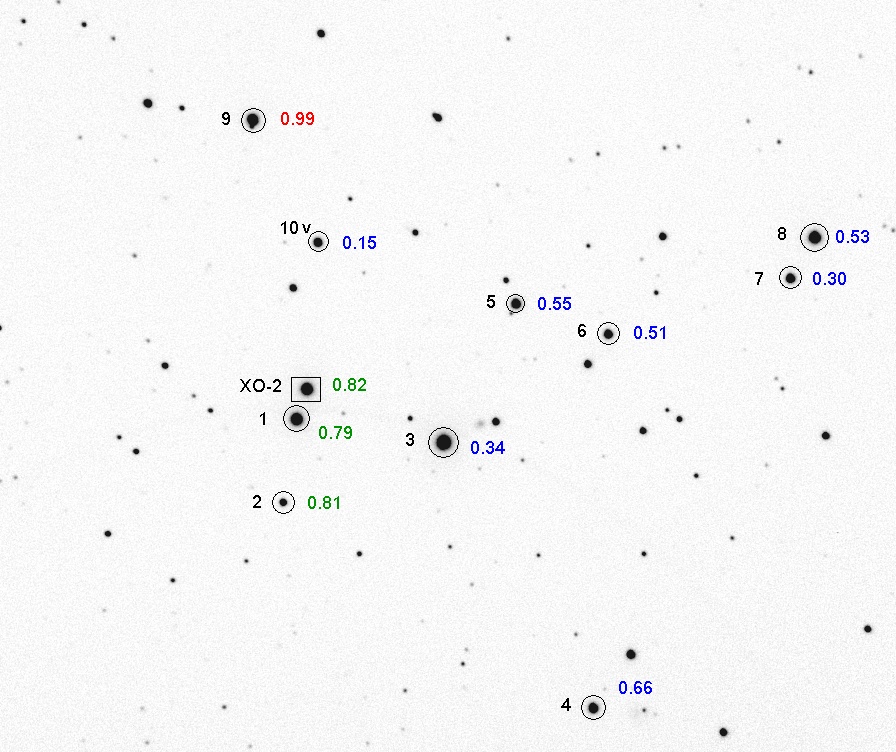
Figure A.03. Star field with B-V color labels. This is a 14.7x12.6 ’arc crop of the full FOV (24x16’arc). North up, east left.

I will describe three ways to evaluate the presence of defects in a master flat field. One technique checks for patterns in magnitude-magnitude plots for two stars in a large set of images. Another method involves observing Landolt star fields and processing them using an all-sky analysis procedure. The third method involves taking a long series of images of a pair of equally bright stars within the FOV without autoguiding and comparing their ratio versus time as they traverse various parts of the CCD pixel field. It resembles the first method except that it makes use of intentional movements of the star field with respect to the CCD pixel field.

Mag-Mag Scatter Plots

There’s a clever “reality check” to see if a drifting star field is producing systematic brightness changes due to flat field errors (thanks, Peter McCullough, for showing me this). I’ll illustrate it with an unfiltered 6-hour observation session of the previous figure’s star field.

The stars in this image were observed to rotate clockwise about the autoguider location in the sky, which was 16.5 ’arc to the south of the main chip’s FOV center. Stars in the center moved ~6 pixels during the 6-hour observing session, and those near the upper edge moved ~9 pixels. If the flat field did a perfect job of correcting all star fluxes to what they would be if they were near the center of the image then this motion would be unimportant. A star near the edge requires a larger flat field correction than a star near the center, and any imperfections in the flat field are likely to affect edge stars more. To see if stars have been correctly flat field corrected we can take advantage of the fact that when a star field drifts any incorrect flat field corrections are likely to differ for stars at different locations.

Consider Stars #5 and #6 (in Fig. A.03). Their measured magnitudes during the entire observing session are plotted in the next figure. Notice how “well-behaved” they are, in the sense that they did not change brightness with respect to each other. This result is unsurprising since the two stars are close together and have similar colors. It shows what can be expected if flat field errors at the two star FOV locations are not present.

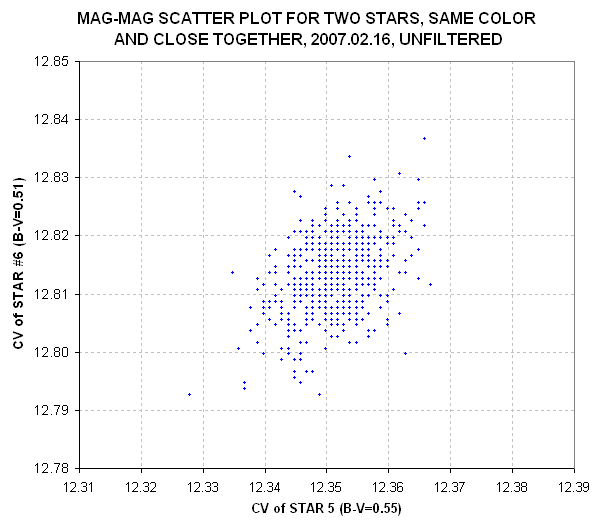
Figure A.04 Mag-mag scatter plot for two stars with same color and close together for the 6-hour clear filter observing session of 2007.02.16.

Figure A.05 shows what happens in a mag-mag scatter plot when one of the stars is near the edge (Star #8) and the other is near the center (Star #5). Keep in mind that for these observations the telescope was configured so that the flat fields had a pattern very similar to those pictured in Fig. A.01, where there’s a smooth fall-off of response from 100% near the center to ~63% near the corners. In other words, the flat field response function is steep near the edges, where Star #8 is located.

In this scatter plot Star #8 (near the FOV edge) exhibits excessive scatter whereas Star #5 (near the FOV center) is well-behaved. Star #8 moved ~8 pixels during the observing session and the flat field correction during this movement ranged from 9.4% to 10.0%. This suggests that the flat field correction was imperfect, and produced an extra component of “magnitude variation” that was not present for stars near the center or the image.

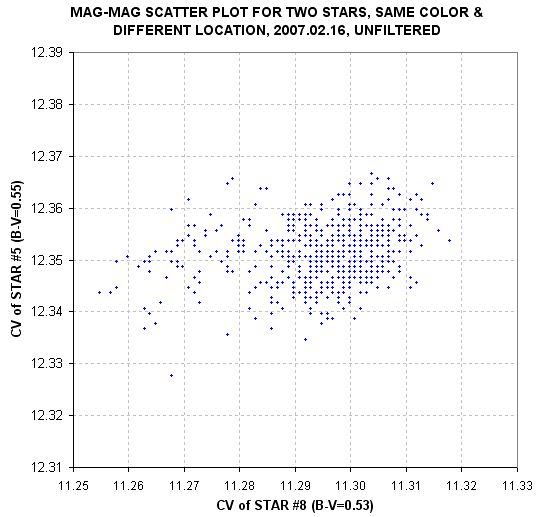
Figure A.05 Mag-mag scatter plot for two stars with same color but far apart (5 ’arc) for the same 6-hour unfiltered observing session of 2007.02.16.

The purpose of the mag-mag scatter diagrams is to detect whether flat field error effects are present. For the case illustrated by the previous two figures there appears to be a problem with stars close to the FOV edge. When this happens stars near the edge should not serve as reference stars since the mag-mag scatter plot does not tell us how to adjust the flat field. This is one reason the target and candidate reference stars should be placed near the FOV center.

All-sky Photometry Method for Flat Field Evaluation

There are 1259 “Landolt stars” that have been calibrated with extreme accuracy (Landolt, 1992). Most of them are in groups of 20 to 50 stars located along the celestial equator at RA intervals of ~1 hour. Most Landolt stars have been observed on several occasions and have been accepted for inclusion when they are found to be constant, but long-term variables are occasionally encountered (I’ve found two). Each group of Landolt stars is spread over an area that is usually larger than a typical FOV. Using my FOV of 11 x 17 ‘arc, for example, it is possible to include 6 to 10 Landolt stars in one image that are bright enough for an amateur to achieve a high SNR (e.g., >500).

Figure A.06: Flat field with V-band filter to be evaluated using Landolt stars.

Figure A.07: Landolt star field at RA/Dec = 15:38:51, -00:19:33. FOV = 11 x 17 ‘arc used in evaluating flat field quality by comparing measured with Landolt magnitudes.

Figure A.06 is a flat field using a V-band filter. It is darkest in the upper-right corner, where a 1.095 flat field correction factor is required.

Figure A.07 is a calibrated image showing 8 Landolt stars. If this image had been calibrated using a good flat field then it should reveal this fact by showing agreement with the Landolt star magnitudes at each of the 8 FOV locations sampled. This is just one of ten sets of images, where each set has been positioned with RA/Dec offsets so as to uniformly sample as much of the CCD area as possible. If there is agreement between all 8 stars and their Landolt V-magnitudes for all 10 image sets then it would be fair to surmise that the flat field is accurate. A more accurate surmise would be that the large spatial wavelength components representing the flat field are accurate. Using this technique there is no way to probe the flat field’s quality at short spatial wavelengths.

In theory a flat field could be constructed by repeatedly dithering RA and Dec until all regions of the CCD have been sampled by Landolt stars. I don’t recommend doing this, for several reasons that are described below. Nevertheless, it is feasible to check the quality of a flat field by observing a Landolt star field with a few carefully selected RA and Dec offsets.

Figure A.07 includes 8 Landolt stars brighter than 13^th magnitude. It was observed with 10 different RA/Dec offsets, producing 70 locations on the CCD pixel field where a measured magnitude could be compared with a Landolt magnitude (the number is less than 80 because some RA/Dec offsets placed Landolt stars outside the FOV). All observations were made with a V-band filter. Star color effects are removed by solving for a star color coefficient in an expression for V-magnitude:

V-mag = 19.670 – 2.5 * LOG₁₀ (S / g) – Kv’ × AirMass – 0.055 × C’

where S is star flux [counts], g is exposure time [seconds], Kv’ is zenith extinction for the V-band filter [magnitude/air mass] and C’ is a linearized version of star color C, defined as C = 0.57 × (B-V) - 0.30. The linearized version is C’ = C + 1.3 × C². The constants 19.670 and -0.055 were derived from a least-squares fitting procedure using the 70 star flux measurements. All images for this session were made near transit, so air mass was constant and it didn’t matter what value was used for Kv’.

If the flat field used in calibrating these images was good then it should be possible to achieve a good quality fit for all 70 Landolt star magnitude measurements. For this set of images the residuals had an RMS deviation of 0.023 magnitude. A plot of these residuals versus star magnitude is shown in Fig. A.08.

In this figure it is apparent that some stars are persistently brighter or fainter than the model fit and this could be due to the star changing brightness during the two decades between the time the Landolt measurements were made (1980s) and the present. It is not unreasonable to hypothesize that a star changed brightness by 0.024 magnitude during that time (this is the largest average difference found from the above fitting procedure). If star brightnesses are adjusted to produce zero averages the RMS scatter becomes 0.017 magnitude. Whichever choice is made the resulting conclusion is approximately the same: the flat field was successful at about the 0.02 magnitude level. The RMS residuals (range = 0.017 to 0.024 magnitude) correspond to ratios within the range 1.6 to 2.2 %.

Does this constitute a validation of the flat field? Not really! After all, the maximum flat field correction for the flat field under evaluation is 9.5%, and the typical RMS variation for star locations is ~1.2%. In other words, the “all-sky photometry method for evaluating a flat field” is simply too imprecise for evaluating typical flat fields. There is little prospect that better quality all-sky photometry can be counted on for improving the value of its use for evaluating flat fields. After all, an RMS scatter in the range 0.017 to 0.024 magnitude is pretty good for all-sky photometry.

Figure A.08. V-magnitude residuals with respect to model fit (using the two parameter values 19.670 and -0.055) plotted versus star magnitude.

This method for evaluating a flat field will only be useful for ruling out the presence of large errors. These large errors are more likely to be present when the flat field has a large amount of vignetting, or when there is reason to suspect the presence of a large stray light component in the flat field. Only when flat field errors of ~3% or larger are thought to be present, or need to be ruled out, will this method for evaluating a flat field be useful.

Star Ratio Changes with Star Field Offsets

The previous section shows, I hope, that attempting to establish a flat field shape using accurate magnitude information of Landolt stars is a too ambitious goal. It may be useful for identifying gross errors, such as those exceeding ~3%, but the approach cannot be used to identify errors of much lower amounts.

In this section we will pursue the less ambitious goal of answering the question:

What are typical error differences in the flat field for randomly-chosen

pairs of pixel location areas?

This question is relevant to the task of producing exoplanet light curves with a minimum of systematic shape errors. After all, if it can be shown that a pair of stars maintain the same flux ratio for many pixel offset settings, then it is fair to assume that image rotation movements of a target star and its ensemble of reference stars will maintain a similar stability of flux ratios.

To perform this test we don’t need Landolt star fields; we only need stars that do not vary on hourly time scales. The previous section dealt with a set of observations of a star field with a variety of position offsets, and since these images have already been processed I will use them in this section to evaluate the new, less ambitious question.

We must keep in mind that every star’s flux measurement is noisy due to Poisson noise, scintillation noise and aperture pixel noise. These sources of noisiness could mask real changes in flux ratios produced by flat field errors. Let’s calculate noise levels from these sources before proceeding with a calculation of observed flux ratio changes.

The images were made with 10-second exposures at air mass ~1.25, so scintillation is estimated to be on the order of 2.5 mmag. Star fluxes ranged from 4100 to 590,000 counts, so Poisson noise is calculated to range from 10.7 to 0.9 mmag, respectively. Aperture pixel noise is calculated to be 0.5 mmag. Each star is therefore expected to exhibit values for fundamental SE that range from ~3 to 11 mmag. Since these noise sources are uncorrelated from star to star, when two stars are compared the magnitude difference should exhibit root-two greater SE, or ~4.2 to 16 mmag. The image sets that were processed in the previous section consisted of 10 images per set, so when average magnitude differences are used the expected SE will be root-10 smaller than for single image differences. Therefore, we can expect to encounter fundamental SE uncertainties of 1.3 to 4.9 mmag when comparing the average magnitude of stars in sets of 10 images.

The measured magnitude differences between star pairs in 10 image groups (10 images per group) are SE = 17, 28, 25, 20, 28 and 24 mmag. These six SE values correspond to six star pairings. The median and average of these six SE values are both 24 mmag. Thus, the measured SE is greater than expected from the assumed Poisson noise, scintillation noise and aperture pixel noise. It is possible that scintillation noise was greater than usual for the observing session. Otherwise I would have to conclude that the flat field error map exhibited large variations, such as 17 mmag (1.6%).

The suggestion that the flat field error map has a 17 mmag RMS variation can be used to infer the magnitude of systematic light curve variations if the image rotation and movement across the pixel field was comparable to the spacing of stars used to derive the 17 mmag value. The average spacing between stars is ~ 5 ’arc. Typical image movements during a light curve observing session are much less than this. We do not have information about the spatial auto-correlation distances for these flat field errors, so it is not possible to predict the magnitude of systematic light curve errors for typical movements. A proper analysis would correlate magnitude differences with star separation distance, and I have not done this.

It could be argued that the spatial structure of the flat field response distribution can be used as a guide in estimating the spatial structure of the flat field error map. If this is justified, then visual inspection of Fig. A.06 suggests that the error map is dominated by spatial structures having wavelengths ~5 ’arc. Since typical movements of the star field (for my present polar alignment) are << 1 ’arc (they’re on the order of 0.1 ’arc), a bold prediction could be made that I should encounter systematic light curve errors <4 mmag (and possible ~0.4 mmag).

The reader is invited to pursue an investigation of their own system’s flat field errors using their own observations and guided by the ideas presented in this appendix. No doubt, there must be other ideas to be guided by, and the author would appreciate feedback on any results or ideas on this matter.

APPENDIX B – Selecting Target from Candidates List

This appendix is for those few amateurs who are privy to a secret list of possible exoplanet transits maintained by professionals who operate wide-field camera surveys. As I write this only the XO Project produces such a list for use by a small group of amateur observers. However, I anticipate that in the future professional teams with survey cameras will solicit amateurs to conduct follow-up observations using their secret candidate lists. When that happens, the amateurs invited to join those extended teams will want to learn how to wisely choose candidates from the list for each night’s observation.

The candidate list is based on wide field camera surveys with poor spatial resolution but good sensitivity. Because of the poor spatial resolution most “candidates” are faint eclipsing binaries whose light is blended with a brighter star that is mistaken by the survey candidate analysis software for being the eclipser. This common situation is called “EB blending.” The main role for amateur observers is to determine which star is fading and by how much. As a bonus the amateur light curve can reveal the shape of the event, and if it is closer to flat-bottomed than V-shaped, as well as shallow, there will be heightened interest in additional observations.

If you’re going to spend 6 or 8 hours observing a candidate it is reasonable to spend a few minutes evaluating the merits of various candidates on a list showing predicted transits for the night in question. Exoplanet candidates derived from survey camera data will contain the following information for each candidate: periodicity (P), length of transit (L), depth (D) and maybe star color J-K. Let’s assume that an ephemeris of predicted transit times is available for each UT date (and possibly restricted to what’s observable from the observer’s site). On any given night there may be half a dozen candidates with transits that can be observed. If J-K is not given then the observer should obtain it from a star catalog (such as TheSky/Six). The following graph can be used to identify candidates that have transit lengths compatible with the transit being from an exoplanet instead of an eclipsing binary that is blended with another nearby star (giving the appearance of a small depth).

Consider the following information for a survey candidate that has never been observed in a way that defines its LC accurately: P = 3.9 days, length of transit = 2.2 hours, J-K = 0.41. Using this figure locate the point for J-K = 0.41 and P = 3.94. Then read the y-axis value of 2.8 hours. This is the longest possible length for a transit (i.e., it’s the length for a central transit). The survey catalog’s measured length of 2.2 hours is less than this maximum length, which is consistent with an exoplanet transit.

Consider another survey candidate example: P = 2.4 days, length = 2.6 hours, J-K = 0.60. Referring to the graph again we find that the longest possible transit is 2.1 hours. The survey’s reported length of 2.4 hours is too long. These transit numbers are incompatible with an exoplanet transit, and we may suspect that this is an eclipsing binary that is blended with another nearby star. An “EB blending” situation can lead to an incorrect J-K for the star undergoing transit, so it is still possible that this candidate is an exoplanet; but since there are so many more EB blending situations than exoplanet transit situations the odds favor the EB blending interpretation, and an observer should be wary of investing time in observing such a candidate.

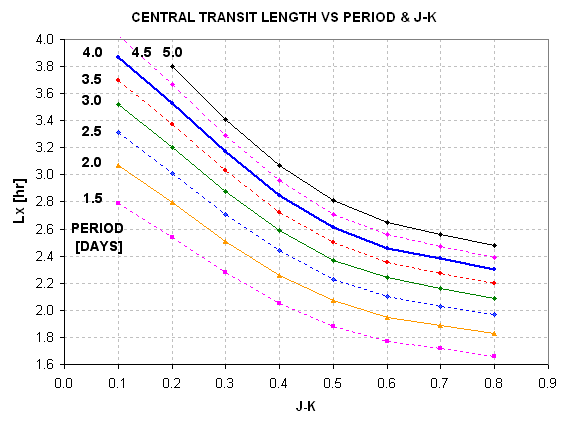
Figure B.01 Central transit length, Lx, versus J-K star color and orbital period.

Although Appendix D contains an extensive treatment of concepts for fitting LCs to exoplanet transit models, I will give a brief description here of the concepts underlying this figure. Main sequence stars, which comprise ~90% of all stars, have sizes and masses that are correlated with their colors. Since J-K colors are available for almost all stars that an amateur will encounter for this purpose I have chosen to use this color instead of B-V. Knowing a star’s J-K means that we can infer the star’s radius and mass (assuming it’s a main sequence star). Knowing the secondary’s orbital period allows us to calculate its orbital radius, using the simple relationship that orbital radius is proportional to (P)^2/3 times (total system mass)^1/3. From orbital radius and period we can calculate the secondary’s orbital velocity, and combining this with the star’s radius we can derive the time it takes for a central crossing.

If we define transit length to be the “full width at 1/3 maximum” for the transit feature then we have a parameter that closely corresponds to the time it takes for the center of the secondary to traverse the transit chord across the star. Exoplanet transits from survey cameras will fold many transit events to produce a less noisy transit shape. It will have a noise level (~5 to 15 mmag) that is not much smaller than transit depth. In practice the transit length listed in the survey candidate catalog will be shorter than contact 1 to contact 4, and is often an approximation of “full width at 1/3 maximum.” To the extent that this is true the above figure will give reliable guidance on maximum possible transit length.

Exoplanet candidate ingress and egress times can be wrong by an hour or two. When planning an observing session for a candidate it is wise to allow extra observing time before ingress or after egress to be sure of capturing it. Otherwise you may issue a “no show” report that can be misleading.

Exoplanet candidate observing can be useful if only a partial transit event is observed. This at least will show which star is undergoing transit, and it is usually possible to categorize the candidate as being an EB blend versus a shallow transit from measured depth of only a part of the transit event. Therefore, when planning a night’s observations it’s OK to selecting a candidate when only part of the predicted transit can be observed.

Many of the considerations presented in Chapter 3 for selecting an exoplanet for a night’s observations also apply to selecting an exoplanet candidate.

APPENDIX D - Planet Size Model

INTRODUCTION

This appendix is long. It has nothing to do with exoplanet transit observing tips, and that’s why it’s in an appendix. I present it for those readers who think it might be fun to play “modeler” and who want to interpret a well-established LC in terms of planet size. I must admit that the simple procedures leading to the final one described here has misled me a few times. However, after each failure I reviewed my assumptions and learned from them. One lesson is that if an internally consistent solution is impossible then consider the star to be “off the main sequence,” where star color to size and mass conversions are questionable. Consider also the possibility that the transits are produced by a triple star system, in which the depth only appears shallow when in fact it is a deep eclipsing binary that is blended with a third star that’s within the photometry aperture (and possibly a close binary with the eclipsing binary pair).

The goal of this appendix is to describe a simple model that I developed for converting a transit light curve (LC) to an estimate of the size of the secondary, which is then used to discriminate between the secondary being an exoplanet versus a small and faint star (i.e., an eclipsing binary system).

A "concept description" section uses actual R-band measurements of an exoplanet to illustrate how a LC can be interpreted. The "model" employs limb darkening relationships for each filter band. The primary star's B-V color (closely associated with spectral type) is used to derive the star's mass and radius, on the assumption that it's a main sequence star (like ~90% of stars). Orbital period is used to calculate orbital velocity (assuming a circular orbit). The planet's radius and "central miss distance" (related to inclination) are adjusted to match the LC depth and duration.

A proper solution for planet radius will involve a fit to the entire LC, not a solution based on agreement with the LC’s depth, length and shape parameter that is employed by the simple solution in this appendix. A crude method is presented for determining if the shape is similar to what an exoplanet can produce, versus what a blend of an eclipsing binary (EB) with another nearby star would produce. My shortcuts reduce accuracy, of course, but if an approximate answer is acceptable then the procedure described here may be useful.

Section 1 is a case study that is used to illustrate the concepts employed. Far more steps are shown than would be used in practice. The goal for this section is to determine the size of the secondary (exoplanet or EB binary star).

Section 2 shows how to use information about the LC's shape to assess whether the LC is compatible with an exoplanet or an EB whose light is blended with a nearby star to produce what merely appears to be a small transit depth.

Section 3 is a summary of only those things that need to be done, after the underlying concepts are understood, to convert the basic properties of a LC and star color to a solution for secondary size and likelihood of the transit belonging to an exoplanet versus an EB.

Section 4 describes an Excel spreadsheet that can be downloaded and run to do just about everything described on this appendix. The user enters transit depth, transit length, period and star color (B-V) in cells corresponding to the LC's filter band and a cell displays a 3-iteration solution for Rp/Rj (if a solution exists). It also can be used to assess the likelihood of the LC shape belonging to the exoplanet domain, based on the user's input of a shape parameter, S.

1. CONCEPTS OF LC INTERPRETATION - A CASE STUDY

I like explaining things through the use of a specific example. The reader's job is to "generalize" from the specific. I'm going to treat real observations of a "mystery" star's transit light curve; this way we can grade the results of my crude analysis procedure using a rigorous treatment by professionals.

Let's assume the following:

GIVEN:
    B-V = +0.66 ± 0.05 (which can be derived from J-K)
    orbital period, P = 3.9415 days,
    R-band observations
    transit depth, D = 23.7 ± 0.4 mmag,
    transit length, L = 2.97 ± 0.03 hours (contact 1 to 4).

The D and L values were derived from the transit light curve in Fig. D.01, measured with an amateur 14-inch telescope (pretend you don’t know which star this is).

After a transiting candidate has been observed, and before radial velocity measurements have been made to assess the mass of the secondary, this is all the information we have to work with. Using this limited information there are many steps for interpreting the LC to estimate secondary size, Rp/Rj (exoplanet’s circular radius divided by Jupiter’s equatorial radius).

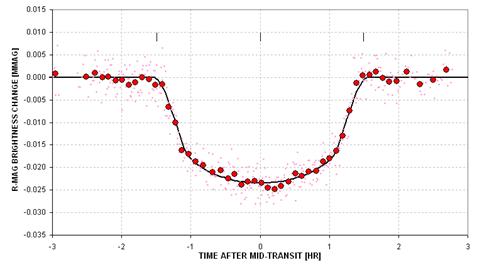
Figure D.01 Transit light curve for a mystery star whose LC we shall try to "solve" using the procedures described on this web page.

SOLUTION:

Star's radius, Rstr = 0.99 × sun's radius (based on equation below)

Rstr = 2.23 - 2.84 × (B-V) + 1.644 × (B-V) ² - 0.285 * (B-V)³

Planet radius, Rp/Rj = 1.41 (1st iteration)

Rp/Rj = 9.73 × Rs × SQRT [1 - 10 ^ (1-D/2500)],

which assumes central transit and no limb darkening

At this point we have an approximate planet size. It's a first iteration since limb darkening has been neglected. The next group of operations is a 2nd iteration.

Star's mass, Mstr = 0.97 (times sun's mass)
Mstr = 2.57 - 3.782 × (B-V) + 2.356 × (B-V)² - 0.461 × (B-V)³

Planet orbital radius, a = 7.22e6 [km]
a = 1.496e8 * [Mstr^1/3 × (P / 365.25)^2/3],

where dimensions are P[days], Mstr[solar mass] & a[km]

Transit length maximum, Lx = 3.28 [hr] (corresponds to central transit)
Lx = 2 (Rstr × Rsun + Rp/Rj × Rj) / (2 π a / 24 × P)

where Rsun = 6.955e5 km, Rj = 7.1492e4 km

Miss distance, m = 0.42 (ratio of closest approach to center to star's radius)
    m = SQRT [1 - (L / Lx)² ]

Limb darkening effect, LDe = 1.16 (divide D by this)
    I(m)/I(av) = [1 - 0.98 + 0.15 + 0.98*m - 0.15*m² ] / 0.746, for B-band
           " = [1 - 0.92 + 0.19 + 0.92 × m - 0.19 × m² ] / 0.787, for V-band
           " = [1 - 0.85 + 0.23 + 0.85 × m - 0.23 × m²] / 0.828, for R-band
               "       = [1 - 0.78 + 0.27 + 0.78 × m - 0.27 × m²] / 0.869, for I-band

Corrected transit depth, D = 20.4 mmag (1st iteration for D)

D = D / LDe (this is the D that would have been measured if the star were

uniformly bright)

Planet radius, Rp/Rj = 1.31 (2nd iteration for Rp/Rj)

(Same eqn as above but now assumes m = 0.42 and appropriate limb darkening)

Transit length maximum, Lx = 3.25 [hr] (2nd iteration for central transit length)

(Same eqn as above)

Miss distance, m = 0.405

(Same eqn as above)

Limb darkening correction, LDe = 1.165 (divide D by this)

(Same eqn as above)

No more iterations are needed since the two miss distance results (& limb darkening corrections) are the same. We have a stable solution:

Rp/Rj = 1.306

To assign a SE to this solution it is necessary to repeat the above procedure using a range of values for the measured transit depth and length. When this is done (using an Excel spreadsheet) we get Rp/Rj = 1.306 ± 0.063 (with B-V uncertainty contributing the greatest component of SE). Note that the stated SE doesn't include the uncertainties associated with the equations converting B-V to stellar radius and mass, nor does it allow for the possibility that the star is "off the main sequence."

EVALUATING THE SOLUTION

How good is this result? Let's compare it with a detailed model-fitting analysis by professional astronomers. The "mystery" exoplanet is no mystery. It's XO-1, whose discovery was announced May 18, 2006 and published in the September issue of the Astrophysical Journal by McCullough et al (2006):

http://xxx.lanl.gov/abs/astro-ph/0605414 (abstract), and

http://arxiv.org/PS_cache/astro-ph/pdf/0605/0605414.pdf (complete article).

This article reports that Rp/Rj = 1.30 ± 0.11. This compares well with the simple model result calculated here, of Rp/Rj = 1.31 ± 0.07. (The larger SE for the professional result reflects a realistic assessment of such systematic uncertainties as converting B-V to stellar radius and mass.)

The B-band light curve for XO-1 is measured to have D = 24.8 ± 0.5 and L = 2.95 ± 0.03. For these inputs the procedure described above gives Rp/Rj = 1.29 ± 0.06.

GRAPHICAL REPRESENTATION OF EQUATIONS

The following graphs can be used instead of the equations for deriving star radius, mass and limb darkening correction (derived from Allen's Astrophysical Quantities, Fourth Edition, 2000):

Figure D.02. Converting star color B-V to stellar radius (assuming main sequence).

Figure D.03. Converting star color B-V to stellar mass (assuming main sequence).

Figure D.04. Converting miss distance and filter band to intensity at that location, normalized by disk-average intensity (assuming a sun-like star).

The following two figures show how transit shape and depths could behave when the miss distance changes from near-center to near-edge. These are real measurements (graciously provided by Cindy Foote) that were categorized as EB based on the depth values. The concept is the same, whether it's an exoplanet or small EB, because in both cases a central transit should produce a greater loss of light in B-band than R-band, and for a near-edge transit the reverse is true.

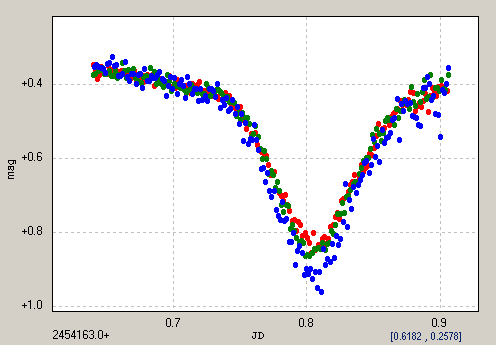
Figure D.05. Transit depth is greatest for B-band, consistent with miss distance <0.73 (courtesy of Cindy Foote).

Figure D.06. Transit depth is greatest for R-band, consistent with a miss distance >0.73 (courtesy of Cindy Foote).

2. VERIFYING THAT LIGHT CURVE SHAPE IS NOT AN E.B. BLENDING

Wide-field survey telescopes provide an efficient means for detecting stars that are undergoing periodic fades with depths small enough to be caused by an exoplanet transit (e.g., depth < 30 mmag) A fundamental limitation of such a survey is that in order to achieve a wide field of view the telescope's resolution is poor, and this leads to many "false alarms" due to the "blending" of light from stars within the resolution circle. If, for example, the resolution circle has a radius of 1 'arc and the flux from all stars within this circle corresponds to ~11th magnitude, it is common for several stars to be present within the resolution circle that are fainter than 11th magnitude but with fluxes that add up to 11th magnitude. If this situation occurs, and if one of those stars is an eclipsing binary (EB) with a large transit depth, the transit depth measured by the survey telescope will be smaller, and possibly small enough to resemble one produced by an exoplanet. This is a common occurrence.

There are two blending situations that need to be considered: 1) the EB is part of a triple star system, so the blending star is too close to the EB to be resolved by ground-based telescopes, and 2) the EB and the blending star are far enough apart (usually gravitationally unrelated but close together in our line-of-sight) that their angular separation is within the resolution limits of ground-based telescopes. The second of these blending situations is probably more common than the first.

When a survey telescope produces many candidates per month it is not feasible to rule out an EB explanation for each one by measuring radial velocities during the course of a few nights with a telescope large enough to produce spectrograms that have the required accuracy. Although radial velocity measurements would allow the determination of the secondary's mass, and thus distinguish between EB and planet transits, large telescope observing time is too costly for such an approach.

A better alternative is to perform follow-up observations of the survey candidates using telescopes with apertures sufficient to identify the most common blending situation. Amateurs with telescope apertures 8- to 14-inches, for example, have more than sufficient resolution to determine which star within the survey's resolution circle is undergoing transit, thus easily identifying most cases of EB blending. These amateur telescopes also have sufficient SNR for an 11th magnitude star, for example, to allow the transit light curve to be determined with good enough quality to sometimes identify the presence of a triple star system EB. There may be more cases of triple star EBs that resemble exoplanet transits than there are actual exoplanet transits. Therefore, it is important to be able to interpret a transit light curve to distinguish between a triple star EB and an exoplanet.

This section demonstrates how amateurs can distinguish between exoplanet light curves and "EB triple star blended light curves" of similar depth, so that additional amateur observing time is not wasted on non-exoplanet candidates.

As an additional check the shape of the measured transit light curve can be compared with a model calculation. First, let's consider LC shapes for various sized secondaries (either an exoplanet or EB star) transiting across the center of the star they orbit. The following figure was derived from a model that used sun-like R-band limb darkening.

Figure D.07. Model light curves for central transits by different sized secondaries. An R-band sun-like limb darkening function was used.

First contact occurs when the intensity begins to drop, and second contact can be identified by the inflection where the slope changes from steep to shallow. A "shape" parameter is defined as the ratio of time the secondary is partially covering the star to the entire length of the transit (e.g., contact 1 to contact 2 divided by contact 1 to mid-transit). For example, in the above figure consider the trace for Rp/Rstr = 0.12: contact 1 and 2 occur at -0.55 and -0.44, and contact 1 to mid-transit is 0.55. For this transit the shape parameter is S = (0.55-0.44) / 0.55 = 0.20.

Let's estimate the shape parameter for a real transit.

In Fig. D.08 my readings of contact 1 and 2 are -1.48 and -1.05 hour. The shape parameter is therefore 0.29 (0.43 / 1.48). Assigning SE uncertainties and propagating them yields: S = 0.29 ± 0.01.

Figure D.09 shows how the shape parameter varies with secondary size for central transits.

Figure D.08. Measured light curve with the contact times indicated.

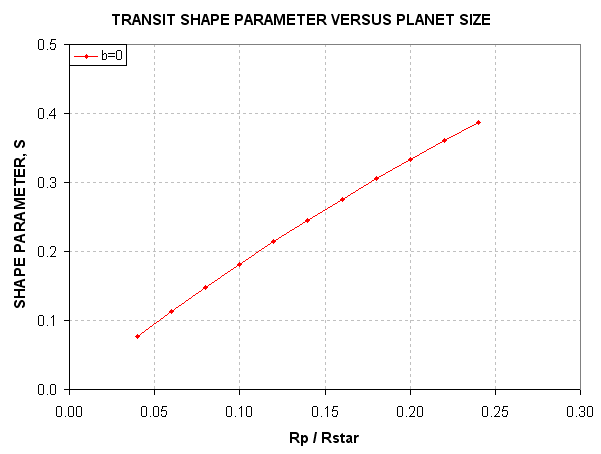
Figure D.09. Shape parameter, S, versus planet size for central transits.

We next consider how the LC shapes vary with miss distance (also called “impact parameter”). We'll adopt one secondary size and vary the miss distance.

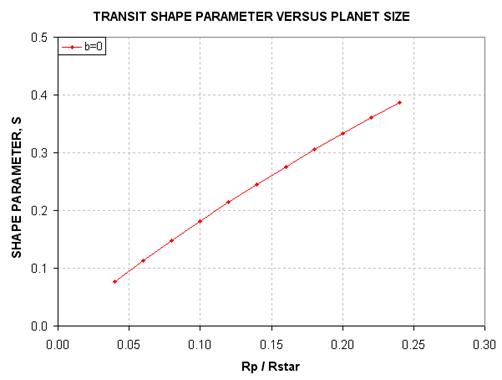
Figure D.10. Shape of LCs for various miss distances (b) and a fixed secondary size of Rp/Rstr = 0.08.

(Note that I’ve changed terminology for "center miss distance" from m to b. Sorry, but I used both symbols for this parameter while calculating the graphs.)

The following figure summarizes the dependence of S on many choices for planet size and miss distance.

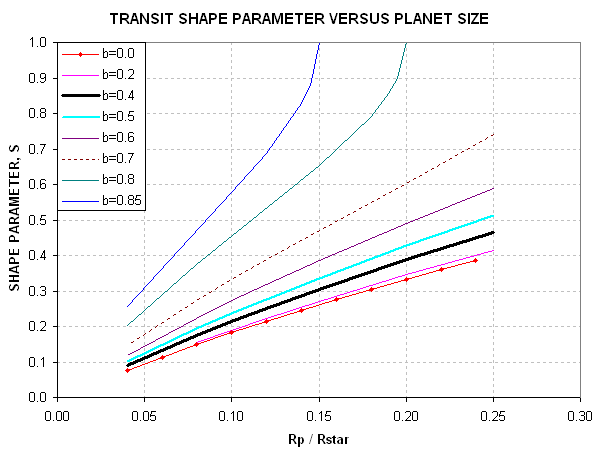
Figure D.11. Shape parameter for a selection of secondary sizes and center miss distances, b.

Recall that for this LC we determined that S = 0.29 ± 0.01. The shape alone tells us that Rp/Rstr < 0.17. From the previous section we derived m = b = 0.40 (the thick black trace in the above figure), so this means Rp/Rstr ~ 0.13. It's not our purpose here to re-derive Rp/Rj, but let's do it to verify consistency. Rp/Rj = 9.73 × Rp/Rstr × Rstr/Rsun = 9.73 × 0.13 × 0.99 = 1.25. This is smaller than 1.31 derived from the transit depth, but notice that the 1.25 estimate came from the light curve shape, S, and extra information about miss distance. The consistency check is successful.

Our goal in this section is merely to distinguish between exoplanet light curve shapes and EB shapes. It will be instructive to consider secondaries at the threshold of being a star versus a planet. This is generally taken to be Rp/Rj ~1.5. For such "threshold secondaries" the Rp/Rstr will depend on the size of the star, which in turn depends on its B-V (spectral type). Let's list some examples, going from blue to red stars.

       Blue star:      (B-V ~ 0.30, spectral type F1V), Rstr/Rsun ~1.5, Rp/Rstr ~0.10
       Sun-like:         (B-V ~ 0.65, spectral type G2V), Rstr/Rsun ~1.0, Rp/Rstr ~0.15
       Red star:         (B-V ~ 1.20, spectral type K6V), Rstr/Rsun ~0.7, Rp/Rstr ~0.22

The following figure shows the dependence of "threshold secondary" Rp/Rstr versus B-V.

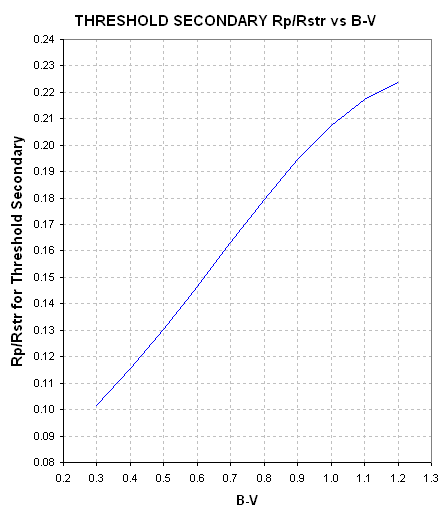
Figure D.12. Relationship of "threshold secondary" Rp/Rstr versus B-V.

In order to use the above figure to distinguish between exoplanet versus EB shapes we need to take into account the primary star's color. For example, if B-V is sun-like, we can draw a vertical line at Rp/Rstr = 0.15 and consider everything leftward to be exoplanets and everything rightward to be EBs. Similarly, for any other B-V a vertical line can be placed upon this figure to show the domains where exoplanets and EBs are to be found, as Fig.’s D.13a,b illustrate.

Since XO-1 has B-V = 0.66 ± 0.05 we can use the left panel to determine that it must be an exoplanet. This determination is based on the shape parameter, S, and the miss distance that was determined from Section 1 (plus the B-V color for XO-1). Even if we hadn't performed a solution for miss distance we could say that's it was likely that the B-V and S information was in the exoplanet domain. If S were slightly smaller, say 0.27, then there would be no dispute about the light curve belonging to an exoplanet. (Well, all this is subject to my model assumptions, such as the "main sequence" one.)

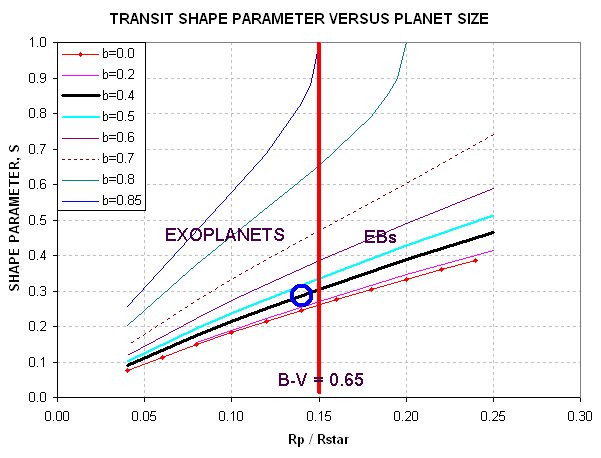
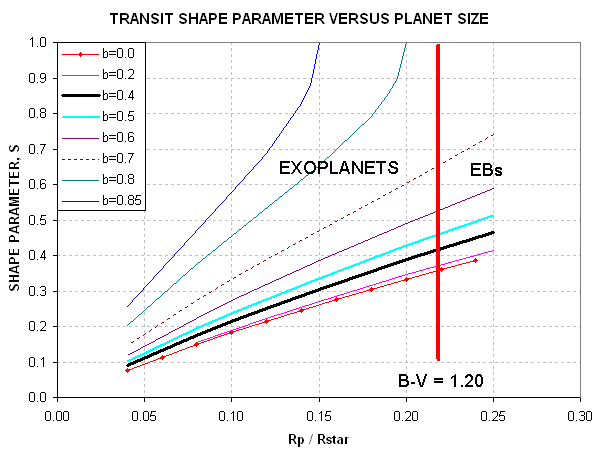
Figure D.13a,b. Domains for distinguishing exoplanets from EBs based on B-V, shape parameter S, and miss distance b, for two examples of B-V. The blue circle in the left panel is located at the measured shape and center miss distance for XO-1.

There's another graph that can be used for the same purpose as the previous ones, and I think it's much more useful than the graphs in the previous figure because it doesn't require knowledge about miss distance. Instead, it requires knowledge about transit depth, D, which is easily measured.

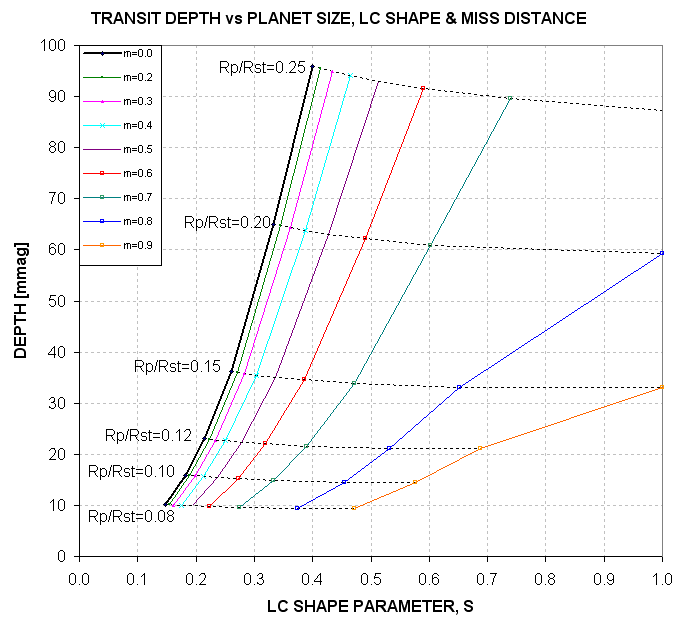
Figure D.14. Domains for exoplanets and EBs, using parameters S and D as input (yielding Rp/Rstr and miss distance as answers).

This figure requires knowledge of transit depth, D, instead of miss distance. This is better since D is easily determined by casual inspection of a LC. The shape parameter S is also easily determined by visual inspection. Therefore, without any attempts to "solve" the LC this plot can be used to estimate Rp/Rstr and miss distance. Then, by knowing B-V we can specify an Rp/Rstr "threshold secondary" boundary in the figure that separates the exoplanet and the EB domains.

Consider the previous example, where XO-1 was determined to have S = 0.29 and D ~ 24 mmag. Given that B-V = 0.66 we know that a "threshold secondary" will have Rp/Rstr = 0.156 (cf. Fig. D.06). Now, using the above figure, draw a trace at this Rp/Rstr value, as in the following figure.

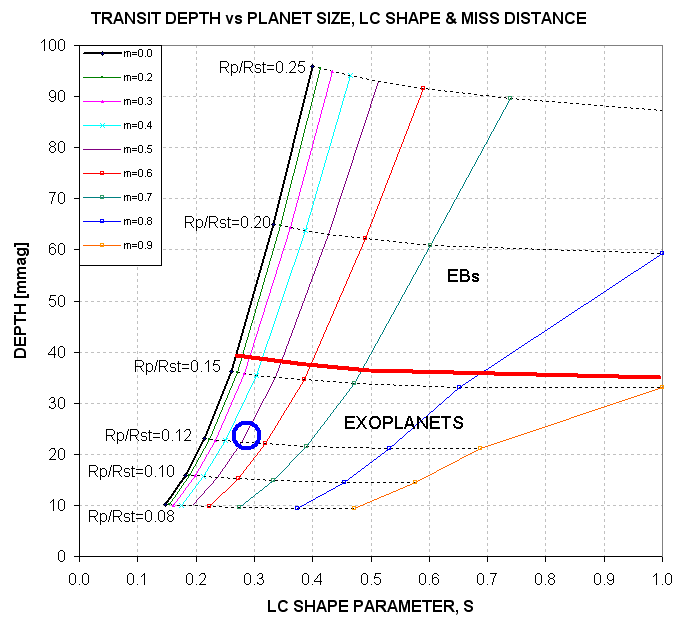
Figure D.15. Domains for exoplanets and EBs for independent variables S and D with a "threshold secondary" Rp/Rstr domain separator (thick red trace) at Rp/Rstr = 0.16, corresponding to B-V = 0.66. The blue circle corresponds to the S and D location for XO-1.

From this graph it is immediately apparent that, subject to the assumptions of the model, XO-1 is an exoplanet instead of an EB. This conclusion does not require solving the LC for Rp/Rstr, as described in Section 1. Indeed, this graph gives an approximate solution for miss distance, m = 0.5 (not as accurate as the solution in Section 1, but somewhat useful).

Here's a handy plot showing "threshold secondary" boundaries for other B-V values.

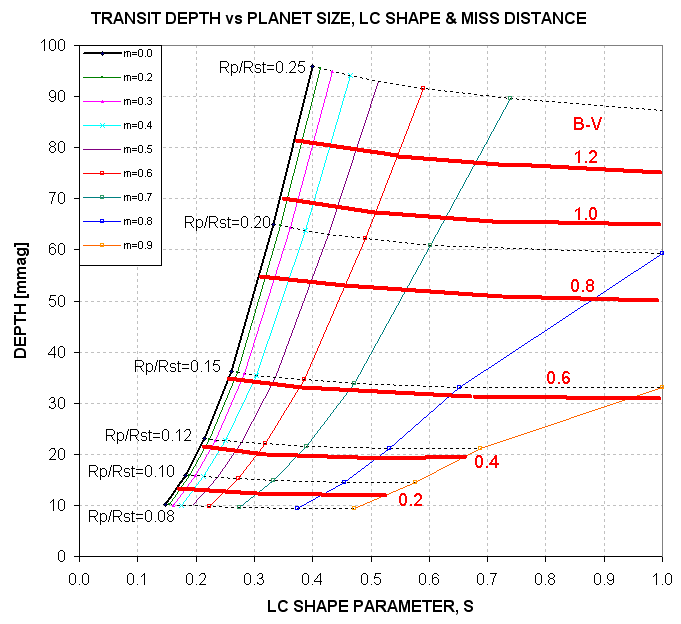
Figure D.16. The thick red traces are "secondary threshold" boundaries, labeled with the B-V color of the star, above which is the EB realm and below which is the exoplanet realm.

This figure allows a quick assessment of a LC's association with an exoplanet versus an EB. If the LC is an EB blend, such as the triplet case described by Mandushev et al (2005), there may not be a "solution" using either the above figure or the analysis of Section 1. To assist in evaluating this it is helpful to have transit light curves for more than one filter band.

Again, this procedure is only as good a guide as the underlying assumptions, the principal one bring that the star undergoing transit is on the main sequence.

3.0 SUMMARY OF TRANSIT LIGHT CURVE ANALYSIS

Much of the preceding was meant to show the underlying concepts for quickly evaluating a transit LC. It may have given an unfair impression of the complications involved. This section will skip the explanations for "why" and just present a sequence of what to do, like a cookbook. The figures needed by these steps are repeated after the instructions.

1) Determine the candidate star's B-V (OK to derive it from J-K)

2) Use the measured LC to determine transit depth, D, and shape parameter, S

2) Using D and P to determine if the LC is likely to be an exoplanet, or EB, or neither (cf. Fig. D.17)

3) If the LC is for an EB, no more analysis is needed. If it's an exoplanet, then proceed

4) Use the Excel spreadsheet (link below) to convert B-V, D, L and filter band to Rp/Rj and miss distance,

OR, do it manually by following the steps below...

4) Determine the star's radius, Rstr, and mass, Mstr, from B-V (cf. Fig. D.18)

5) Calculate 1st iteration of Rp/Rj, using following equation:

Secondary size, Rp/Rj = 9.73 × Rstr × SQRT [1 - 10 ^ (-D/2500)]

6) Calculate secondary's orbital velocity, central transit length and miss distance using these equations:

Planet orbital radius, a = 1.496e8 × [Mstr^1/3 × (P / 365.25)^2/3], where P[days],

Mstr[sun's mass] & a[km]

Transit length maximum, Lx = (Rstr × Rsun + Rp/Rj × Rj) / ( π a / 24 × P) where

Rsun = 6.955e5 km, Rj = 7.1492e4 km

Miss distance, m = SQRT [1 - (L / Lx)²]

7) Using the miss distance and filter band, determine limb darkening effect, LDe (cf. Fig. D.19)

8) Convert the measured transit depth D to a value that would have been measured if there were no limb darkening, using the following eq:

D' = D / LDe

9) Repeat steps 5, 6 and 7 using D' instead of D.

10) If step 7 LDe is the same as the 1st time, then there's no need for additional iterations. The last calculated Rp/Rj is the answer. Otherwise, repeat steps 5-8 until a stable solution emerges.

Figure D.17. If the D/S location for the LC is above the red line corresponding to the star's B-V, then it's probably an EB. If D/S is below then it's probably an exoplanet. If it is to the left of the upward sloping trace (central transit), then there's no solution, and you may be dealing with an EB blending or triple star system.

Figure D.18. Star's radius and mass from B-V.

Figure D.19. Limb darkening effect, LDe, versus transit miss distance and filter band.

This completes the summary of what is done to assess a transit LC to determine if it's due to an exoplanet or EB, and if it's an exoplanet to determine its size. The purpose of this appendix has been to demonstrate that a simple procedure can be used to guide the choice of survey candidates for a night's observing in order to avoid spending time on unlikely (EB blend) candidates.

4.0 EXCEL SPREADSHEET

Now that you understand the concepts I can save you time by offering an Excel spreadsheet that does most of what's described in this appendix. The user simply enters light curve depth D, length L, and star color B-V in the appropriate cells and the spreadsheet calculates a 3-iteration solution for Rp/Rj (provided a solution exists). Here's the link for the Excel spreadsheet that does everything described in Section 1: http://brucegary.net/book_EOA/xls.htm

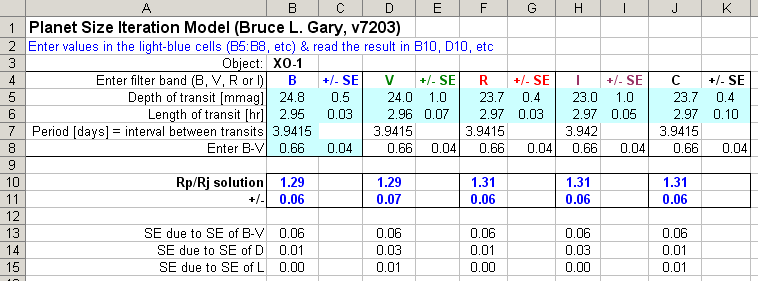
Figure D.20. Example of the Excel spreadsheet with XO-1 entries for several filter bands (B5:C8 for B-band, etc) and the Rp/Rj solution (B10:B11 for B, etc).

The line for SE of "Rp/Rj solution" is based on changes in D, L and B-V using their respective SE. In this example note that the Rp/Rj solutions for all bands are about the same, 1.30. This provides a good "reality check" on data quality as well as the limb darkening model. Rows 13-15 show the SE on Rp/Rj due to the SE on B-V, D and L separately. The largest component of uncertainty comes from B-V. Even if B-V were known exactly there's an uncertainty in converting it to star radius and mass, given that the "main sequence" of the HR diagram consists of a spread of star locations and there's a corresponding spread in the relationship between radius versus B-V and mass versus B-V.

A future version of this spreadsheet will include a section for the user to enter a transit shape parameter value, S, and an answer cell will show the likelihood of S/D being associated with an exoplanet versus an EB. I also plan on expanding the limb darkening model to take into account limb darkening dependence on star color.

APPENDIX E – Measuring CCD Linearity

The maximum ADU counts that can be read out of a 16-bit CCD is 65,535. It is commonly understood that you shouldn’t trust readings greater than about half this value, ~35,000 counts, due to something called “non-linearity.” Whereas you can trust ratios of star fluxes when none of them have maximum counts, Cx, greater than 35,000, when one of them has a Cx >35,000 it’s measured flux is probably smaller than it should be. Only for a hypothetical CCD that is linear all the way to 65,535 counts can you trust star fluxes with Cx values in the range ~35,000 to 65,534 counts.

Don’t believe this! I was pleasantly surprised with a measurement showing that my CCD is linear all the way to ~59,000 counts! The implications for knowing this are significant. If it’s true that you can safely use the longer exposure times corresponding to Cx as high as ~59,000 counts, for example, then your observing will be more efficient (less time spent downloading images), your scintillation and Poisson noise will be lower (by up to ~40% for each image), and the importance of readout noise will be less.

I’ll review the cautious reasoning that continues to lead CCD users to be wary of high Cx. Then I’ll illustrate how to measure your CCD’s linearity safety zone.

Cautious Conventional Wisdom

Each pixel is capable of “holding” an approximate total number of photoelectrons. The term “full well capacity” is used loosely to refer to that number. However, we must make a distinction between “full well capacity” and “linear full well capacity.”

A user’s manual may state that your model of CCD has a “full well capacity” of 100,000 electrons, for example. That’s what the SBIG manual states for my ST-8. The manual also states that my CCD’s “gain” is set so that each count represents 2.3 electrons. According to these two numbers “the well is full” at ~43,500 counts (100,000 electrons / 2.3 electrons per count). Since my CCD can produce higher counts I assume that SBIG’s term “full well capacity” was a conservative way of saying that a pixel fills at a linear rate up to 100,000 electrons then becomes non-linear as it continues to fill further. In other words, I assumed the manual meant to say that my CCD’s “linear full well capacity” was ~100,000 electrons. This would imply that my CCD might be linear up to ~43,500 counts, but I remained cautious for a long time by keeping exposures short enough that stars to be used photometrically had Cx less than ~35,000 counts. The fact that stars would produce Cx all the way up to digital saturation (65,535 counts) means that my CCD’s silicon crystal pixels must be capable of holding at least 150,000 electrons at readout time (65,535 × 2.3).

For a long time I neglected to measure my CCD’s linearity thinking that all the specifications in the manual were compatible with the common wisdom of keeping Cx below about half scale in order to avoid non-linearity problems. I also postponed measuring linearity in the belief that it would be difficult. It isn’t, and it can be fun, especially if you learn good things about your CCD.

The following methods are presented in a way that hopefully illustrates properties of CCDs and ways to explore these properties from special observations and analysis. Once this understanding has been accomplished subsequent measurements of linearity will be almost effortless.

Twilight Sky Flats Method

The simplest way to determine how high Cx can be while still being within the linear region is to expose a series of twilight sky flats using exposure times that produce maximum counts, Cx, that span the entire region of interest: 30 to 65 kct (kct = kilo-counts = 1000 counts). Any filter will work, but you’ll have a “stronger” result by using the filter that has the worst vignetting. For me, the I-band filter is slightly worse than the others, with a faintest area to brightest area ratio = 0.79. It’s not necessary to do this for other filters since one photoelectron is the same as another from the standpoint of silicon crystals in the CCD.

Figure E.01. I-band flat field with Cx = 62 kct before and after calibration using a 34 kct Cx flat frame. The faintest area (upper-right) to brightest have a “vignette range” of 21% and 0.2%, implying that the flat field response was reduced 100-fold, to acceptable levels. The CCD appears to be “linear” even for ADU values as high as 62 kct!

Average the images with Cx between 25 and 35 kct, which everyone will accept as being free of linearity problems. Call this a master flat for use with the brighter flat fields. Let’s define “vignette range” to be a percentage version of the faintest to brightest area of the linear master flat. For example, my I-band “vignette range” is 21 % (i.e., faintest to brightest counts = 0.79).

Next, divide a bright flat by the master flat. This can be done by treating the bright flat as a light frame that must be calibrated using the master flat field. (I’m assuming all flats were made using a dark frame at the time of exposure.)

After calibrating all bright flat fields using the ~30 kct master flat you are ready to evaluate linearity for each. Measure the average counts for the regions that were faintest and brightest and express their ratio as a percentage. For example, after calibrating my I-band flat that had Cx = 62 kct I measured the same areas that were faintest and brightest in the master flat (also the same areas that were faintest and brightest in the Cx = 62 kct before calibration), and got a “vignette range” of 0.21 %. In other words, the “vignette range” went from 21% to 0.21% simply by calibrating using the master flat field. That’s a 100-fold improvement, and any flat with residual errors of 0.2% is good! Flat field errors may be present in both flat fields, so it cannot be concluded that both flats are good to 0.2%. The result we’re after, however, is that a flat field with counts as high as 62,000 has the same brightness distribution as the ones having a maximum count of ~35,000 counts. This can be interpreted to mean that my CCD is linear all the way up to ~62,000 counts!

I performed the same analyses using 4 other filters, and they all gave the same result. The only problem encountered with flats having Cx >55 kct was the appearance of hot pixels at three locations (with cold pixels nearby).

Star Flux Ratio versus Maximum Counts Method

This method will involve more analysis, but it will provide more information about how your CCD responds to too much light.

The method involves taking images of two stars in the same FOV with several exposure times. The two stars should have a flux ratio of about 2:1 (magnitude difference ~0.75). Be sure the stars are near zenith; otherwise you’ll have to correct for extinction.

The shortest exposure time should be whatever produces Cx ~10 to 20 kct for the brightest star. I’ll illustrate this method using a pair of stars near NGC 5371 with V-magnitudes ~9.0 and 9.7. My exposure sequence ranged from 5 to 40 seconds.

Figure E.02 is a plot of Cx versus exposure time for the bright star.

Figure E.02. Maximum counts versus exposure time for the brighter of two stars.

Figure E.03. Flux versus exposure time for two stars.

There are two things to notice about Fig. E.02. First, typical Cx flux values increase with exposure time until a “saturation” value of ~60 kct is reached. Second, for each exposure time below “saturation” Cx flux values have a large scatter. The scatter is produced by changes in seeing (or auto-guiding quality). This will be described later.

Figure E.03 plots star flux versus exposure time for both stars. The brighter star shows evidence of “falling below” the fitted line for exposure times 40 and 50 seconds. The fainter star agrees with its fit for all exposures. The reasons for this will become apparent shortly.

The ratio of the two star fluxes is plotted in Fig. E.04.

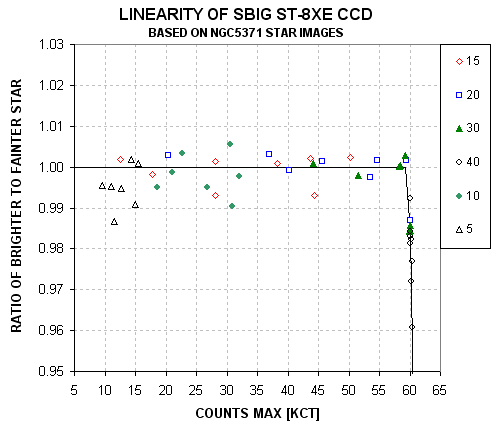
Figure E.04. Ratio of star fluxes (bright divided by faint) versus Cx. The ratio is normalized so that the average unsaturated value is 1.00. The legend shows the association of plotted symbols with exposure time.

When Cx for the bright star exceeds ~59 kct it becomes fainter than would be expected from images having lower Cx values. This suggests that photoelectrons may be “lost” when a pixel accumulates more electrons than a saturation value corresponding to 59 kct for this CCD. This result is what we’re after:

The CCD is linear for stars having Cx < 59 kct!

This conclusion is based on star ratios. Let’s see if we can come to the same conclusion using fluxes from just one star. Figure E.05 plots flux rate versus Cs; “flux rate” is defined as flux divided by exposure time.

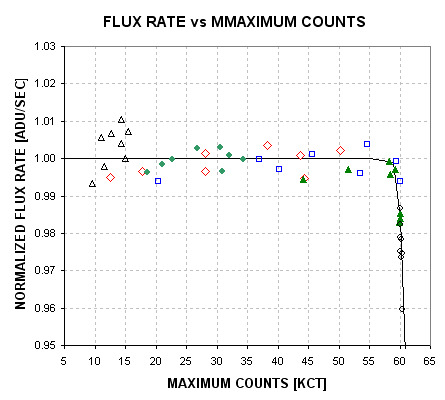
Figure E.05. Flux rate (normalized to 1.00 for unsaturated values) versus Cx, using the brighter star.

As before, “flux rate” versus Cx suggests that the CCD is linear for Cx < 59 kct. The RMS scatter for most of the unsaturated data is ~1/3 %.

Figure E.03 suggests that the faint star is never “saturated” for the images under consideration. Therefore, the FWHM ratio for all images should reveal anomalous behavior for just the bright star. Figure E.06 is a plot of FWHM for the bright star divided by FWHM for the faint star.

When the bright star saturates its FWHM increases. This is what would be expected if the Gaussian shaped point-spread-function becomes “flat topped” when saturation occurs. Another way of showing this is to plot FWHM for the bright star versus FWHM for the faint star, which is shown as Fig. E.07. When both stars are unsaturated the two FWHM values are within the “box” area. Within this box both FWHM variations are correlated, suggesting that either “seeing” or autoguiding varied and affected both stars in a similar way.

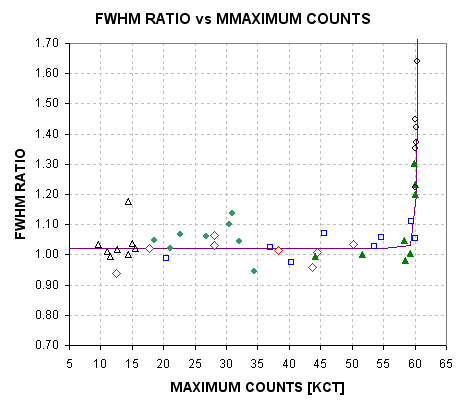
Figure E.06. FWHM for bright star divided by FWHM for faint star, versus Cx for the bright star.

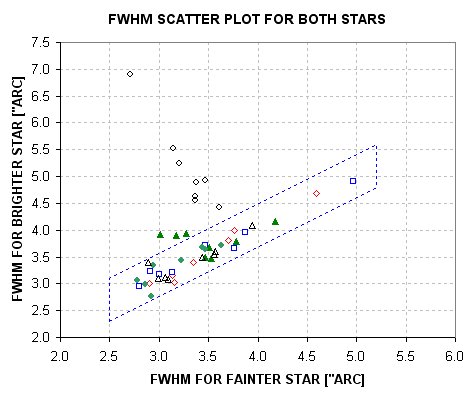
Figure E.07. FWHM for bright star versus FWHM for faint star. The box identifies the situation of unsaturated stars.

Whenever a star is unsaturated, established here by the condition Cx < 59 kct, the following simple relationship should exist: Cx = const / FWHM². As FWHM decreases Cx will increase in order for flux to remain the same. The next figure shows agreement with this theoretical relation; it also shows how Cx saturates when FWHM decreases below a specific value (different for each exposure time).

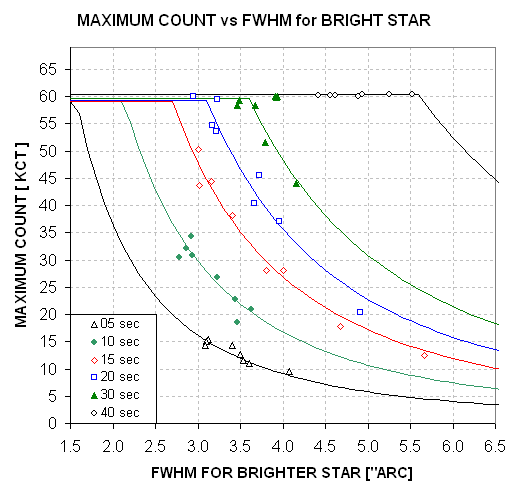
Figure E.08. Cx versus FWHM for the bright star for a selection of exposure times (color coded with exposure times given by the legend). Model fits are explained in the text.

This plot demonstrates that the brightest pixel for a star will increase until the pixel’s “well is full.” For this CCD “fullness” occurs when 159,300 electrons have accumulated (59,000 × 2.7 electrons per ADU, where 2.7 electrons per ADU is the “gain” I measured from the same images). But what happens to photoelectrons that are added after the pixel’s well is full? In theory these additional electrons could simply migrate to nearby pixels and still be counted when the photometry measurement is made. To investigate this we need to see how flux ratio varies with exposure time.

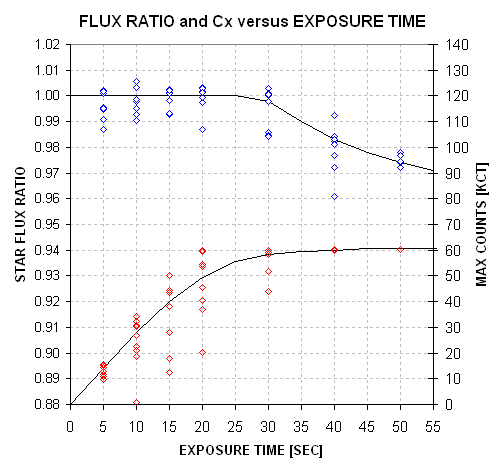
Figure E.09. Star flux ratio (blue) and bright star’s Cx (red) versus exposure time.

When exposure time is 50 seconds the bright star is “saturated” in every image; nevertheless, the ratio of fluxes is affected only slightly! This means that after a pixel’s well fills additional electrons migrate to nearby pixels, and only a small percentage are “lost.” If linearity is defined as <2% departure from linear then this CCD is linear even for conditions associated with the longest exposure images of this analysis. Figure E.10 is a point-spread-function cross-section of the bright star that is saturated in a 50-second exposure. Even this star’s image produces a flux that is low by only 2%.

The statement that the CCD is linear whenever Cx <59 kct is conservative, since saturation above this value may depart from linear by only a small amount.

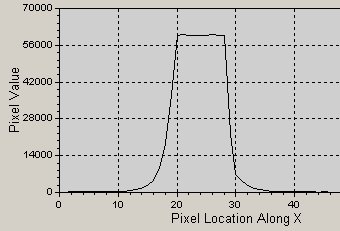
Figure E.10. PSF of a saturated star (the bright star) with Cx = 60.3 in a 50-second exposure. The flux of this star is only ~2% low compared with an extrapolation of what it should be based on measurements with the CCD in the linear region.

Conclusion

I conclude that flux measurements with this CCD are “linear” to ~1/3 % for all Cx up to 59,000 counts. For a CCD gain of 2.7 electrons/ADU, the 59,000 counts corresponds to ~159,000 electrons. The measurements reported here therefore show that my CCD has a “linear full well capacity” of ~159,000 electrons. This is more than the “full well capacity” of 100,000 electrons listed in the manual, which shows that SBIG was being conservative in describing this CCD model.

The various methods for assessing non-linearity can be summarized:

1. Flat field method safe to 62 kct

2. Two Star flux ratio vs Cx safe to 59 kct

3. Star flux rate vs Cx safe to 59 kct

In no instance is there evidence to support the “common wisdom” that to avoid non-linearity effects it is necessary to keep Cx < 35 kct.

Each observer will want to measure their CCD linearity in ways that reveal safe Cx limits. The payoffs are significant. By adopting higher Cx limits longer exposures are permissible, and this reduces scintillation per image, it reduces Poisson noise per image, it reduces the importance of read noise and it improves “information rate” (due to smaller losses to image download time).

GLOSSARY

2MASS: Two Micron All-Sky Survey; a catalog of point sources (stars) and extended sources (galaxies) covering the entire sky using filters J, H and K. Of the 2.1 billion sources, more than 500 million are stars. J and K magnitudes can be converted to B, V, Rc and Ic magnitudes for most sources. Therefore, J-K star colors can be converted to B-V and V-R star colors, which is useful since all stars that amateurs will want to use for reference are in the 2MASS catalog.

air mass: Ratio of number of molecules of air intercepted by a unit column traversing the atmosphere at a specified elevation angle compared with a zenith traverse. An approximate formula for air mass is secant (zenith angle), or 1 / sine (elevation angle). Because of the Earth’s “curvature” the maximum air mass for dry air is ~29 (tabulations are available). To the extent that dust and water vapor contribute to line-of-sight extinction the above formulae are a better approximation than air mass tables, since the scale height for dust and water vapor is much smaller in relation to the Earth’s radius than the scale height for dry air.

all-sky photometry: Use of a telescope system for transferring standard star magnitudes (such as Landolt stars) to stars in another region of the sky with allowance for differences in atmospheric extinction. c.f. photometry

ADU: Analog-to-digital unit, also called a “data number” and “count,” is a number read from each pixel of a CCD camera (using an analog-to-digital converter) that is proportional to the number of electrons freed by photons (photoelectrons) at that pixel location. The ADU count is the number of photoelectrons divided by a constant of the CCD called “gain” (which is inversely proportional to an amplifier’s gain).

artificial star: Replacement of a pixel box (upper-left corner) with values that appear to be a star that has a specific peak count (65,535) and Gaussian FWHM (such as 4.77 pixels). The artificial star can be used with a set of images to monitor changes in cloud losses, dew accumulation losses, as well as unwanted photometry losses produced by image quality degradation.

aspect ratio: Ratio of a PSF’s widest dimension to its narrowest, usually expressed as a percentage. Anything below 10% is good (i.e, close to circular).

atmospheric seeing: Apparent width (FWHM) of a star recorded on a CCD exposure using a telescope with good optics and collimation and short exposures (0.1 to 1 second). “Seeing” (as it is often referred to) will depend on exposure time and elevation angle. Seeing FWHM increases approximately as a constant plus sqrt(g), where g is exposure time. Seeing FWHM also increases with air mass as approximately airmass^1/3. Amateurs using CCDs usually say the seeing is good when FWHM <3.0 ”arc. Professionals would say the seeing is good when FWHM <1.0 ”arc. Seeing degradation is due mostly to ground-level temperature inhomogeneities caused by wind-driven turbulence. The scale height for this component of seeing degradation is ~7 meters. Other components of seeing are at the top of the “planetary boundary layer” (~5000 feet), and tropopause (25,000 to 55,000 feet).

binning: Combining of groups of pixels, either 2x2 or 3x3, during the readout phase of collecting electrons from pixels to an output register for the purpose of achieving faster image downloads that have less readout noise, used when the loss of spatial resolution is acceptable.

blackbody spectrum: Plot of power (energy per unit time) radiated by a 100% emissive material (such as an opaque gas) per unit wavelength, versus wavelength. A version also exists using “power per unit frequency.” A star’s atmosphere is 100% emissive (no reflections) and radiates with an approximate blackbody spectrum. Narrow absorption lines are produced by atoms and molecules at higher altitudes and cooler temperatures; they absorb and re-emit at their cooler temperatures (in accordance with a blackbody spectrum determined by their cooler temperature). c.f. Fig. 14.05.

blue-blocking filter: A filter that passes photons with wavelengths longer than ~490 nm. A BB-filter passes ~90% of a typical star’s light and during moonlight it blocks most of the sky background light coming from Rayleigh scattered moon light.

CFW: Color filter wheel.

check star: Another star in the same set of images as the target star which is processed using the same reference stars (reference stars are sometimes called “comparison” stars for out-of-date reasons). Precision exoplanet photometry usually does not make use of check stars because at the mmag level of precision every star will have a unique dependence on air mass due to its color difference with the reference stars. A check star can provide a false sense of security that systematic errors are not present, or a false sense of alarm that systematics are present. The use of check stars is left-over from variable star work, where mmag systematics are unimportant.

clear filter: A filter that passes most of the light within the wavelength region where CCD chips are sensitive. A clear filter is used instead of no filter (unfiltered) in order to achieve “parfocality” with the other filters (two filters are parfocal when they require the same focus setting).

confusion: A technical term referring to the presence of a background of faint stars (or radio sources) that alter the measured brightness of an object. The only way to reduce confusion is to improve spatial resolution. Wide-field exoplanet survey cameras have a high level of confusion, leading to the need for amateurs to detect EB blending situations.

CSV-file: Comma-separated-variable file, in ASCII (text) format.

dark frame: CCD exposure taken with the shutter closed. A “master dark frame” is a median combine of several dark frames made with the same exposure and same temperature. (Master darks taken at different temperatures and exposure times can be used for pretty picture and variable star work.)

differential photometry: Comparison of flux of a target star to the flux of another star, called reference star, expressed as a magnitude. “Ensemble differential photometry” is when more than one reference star is used (either averaged, or median combined, or flux summed).

dust donut: Shadow pattern of a speck of dust on either the CCD chip’s cover plate (small dust donuts) or a filter surface (larger annular shadows). Flat frames correct for the loss of sensitivity at dust donut locations at fixed locations on the CCD pixel field.

eclipsing binary, EB, EB blend: EB means eclipsing binary. EB blend is when an EB is close to a brighter star that is mistaken by a wide-field survey camera for undergoing a possible exoplanet transit because the fade amount is a much smaller fraction of the light from the blend of stars in the survey camera’s aperture.

egress: Transit interval when the smaller object is moving off the star and only part of the smaller object’s projected solid angle is obscuring star light. Contact 3 to 4.

ensemble photometry: Use of 2 or more reference stars in an image for determining a target star’s magnitude

exoplanet: Planet orbiting another star. Also referred to as an extra-solar planet.

extinction, zenith extinction, atmospheric extinction: Loss of light due to the sum of Rayleigh and Mie scattering plus narrow line absorption; usually expressed in terms of “magnitude per air mass.” An extinction curve is a plot of the logarithm of measured star fluxes versus air mass (usually magnitude, a base-10 logarithm times 2.5, versus air mass). A straight line fit to these data has a slope corresponding to zenith extinction.

extra losses: Reductions of a star’s flux level that are not accounted for by atmospheric extinction. The most common origins for “extra losses” are clouds, dew accumulation on the corrector lens, wind-driven telescope vibrations (smearing the PSF for the affected images) and loss of focus (causing the signal aperture to capture a smaller percentage of the entire star’s flux in the poorly focused images).

filter bands: Wavelength interval with associated response function for the following commonly-used standards: B-band, V-band, Rc-band, Ic-band, BB-band, J-band, H-band and K-band. CV-magnitude begins with observations using a clear filter but with corrections designed to produce a V-band equivalent (usually with star color corrections). CR-magnitude is like CV except the goal is an R-band magnitude. BBR-magnitude uses a blue-blocking filter (BB-filter) and is adjusted to simulate R-band magnitude.

flat frame: CCD exposure made of a spatially uniform light source, such as the dawn or dusk sky, often with a diffuser covering the aperture. Flat frames can be made of an illuminated white board, or made pointed at the inside of a dome (“dome flat”). Several flat frame exposures are combined to produce a “master flat.” A master flat is used to correct for vignetting, dust donuts and small pixel-specific differences in bias and sensitivity (QE).

flux: Star flux is defined to be the sum of all counts that can be attributed to a star based on differences with a sky background level that is calculated from the counts in a sky reference annulus.

FOV: Field-of-view

FWHM: Full-width at half-maximum, describing the angular size of the distribution of light on a CCD produced by a point source, i.e., star. c.f. aspect ratio.

gain: For a CCD the term “gain” is the number of photoelectrons required to produce a change of one ADU. Gain can be measured by noting RMS for a subframe of two flat fields subtracted (similar levels) and RMS for the same subframe of two bias frames subtracted. Gain = (Sum of median counts for the flats – sum of median counts for the bias frames) / (RMS for flats ^2 + RMS for bias ^2). c.f. Appendix F.

information rate: Reciprocal of the time it takes to achieve a specified SNR for a specified target star. Alternative observing strategies, as well as alternative telescope configurations (or different telescopes), can be judged using “information rate” as a figure of merit.

ingress: Transit interval when the smaller object appears to move onto the star and only part of the smaller object’s projected solid angle is obscuring star light. Contact 1 to 2.

image rotation: Rotation of the star field with respect to the pixel field during a single observing session; caused by an error in the mount’s polar alignment. The “center” for image rotation will be the star used for autoguiding.

image stabilizer: Mirror assembly that tips and tilts under motor control at a fast rate (typically 5 to 10 Hz) using an autoguide star. It is used to minimize atmospheric seeing movements of a star field. When the star field drifts close to the mirror motion limit a command is issued to the telescope mount motors to nudge the star field back to within the mirror’s range. SBIG makes a good image stabilizer, the AO-7 for regular size CCD chips and the AO-L for large format CCD chips.

impact parameter: “Distance from star center to the transit chord” divided by the star’s radius. An impact parameter of zero is a central transit.

JD and HJD: Julian Date and Heliocentric Julian Date. JD is the time of an event as recorded at the Earth (center). HJD is the time of an event if it were recorded at the center of the solar system. The two vary throughout the year depending on RA/Dec and time of year, but the difference is always < 8.4 minutes.

length of transit: Interval between contact 1 and contact 4. Survey camera lengths may resemble something intermediate between this and the time between contact 2 and 3, due to insufficient SNR.

light curve: Plot of brightness of a star versus time during a single observing session. Abbreviated LC, it is usually representing brightness in terms of magnitude, with increasing magnitude plotted in a downward direction. LCs may be embellished with marks for predicted ingress and egress, or model fits meant to guide the eye to what the observer believes the measurements should convey.

limb darkening: Stellar brightness distribution for a specific wavelength (filter band) expressed as 1.00 at the star center and decreasing toward the edge (caused by star light close to the limb being emitted from higher and cooler altitudes of the stellar atmosphere). An alternative representation is to normalize to the disk average brightness. Two or three constants are sufficient to represent these shapes. Limb darkening functions vary with spectral type.

linearity: The property of a CCD’s readout (ADU counts) being proportional to the accumulated number of photoelectrons in a pixel. A CCD may be linear for readings from zero to ~90% of the maximum reading possible (i.e., ~0.90 × 65,535 = ~59,000 counts). Linearity and saturation have different meanings but are commonly used interchangeably.

magnitude: Ratio of star fluxes converted to a logarithm. Magnitude differences are calculated using the formula: dM = 2.5 × LOG₁₀ (Si / So ), where Si is the flux of star “i” and So is the flux of star “o”. Flux ratio can be calculated from magnitude differences using the following: Si / So = 2.512 ^dM . A mmag = milli-magnitude = magnitude / 1000.

median combine: Finding the middle value in a set of values arranged by value. The median combine process is relatively unaffected by an occasional outlier value whereas averaging is vulnerable to outlier corruption. The standard error uncertainty of a median combine is ~15% greater than the SE of an average, provided all data are belong to a Gaussian distribution (i.e., outliers are not present). A median combine can be performed on a group of images as well as single set of values, since a group of images is just a set of values for each pixel location.

MDL: MaxIm DL, Diffraction Limited’s program for control of telescope, CCD, image stabilizer, focuser, and also image processing with photometry analysis.

Mie scattering: Aerosols (airborne dust) with a circumference greater than the wavelength of light produces Mie scattering. Mie scattering theory actually encompasses all wavelength to circumference ratios, but in common parlance Mie scattering refers to the situation where the wavelength is slightly longer than the circumference. Much longer wavelengths are trivial to treat as mere blocking of light. Rayleigh scattering is a subset of Mie scattering theory reserved for the case of wavelength much smaller than aerosol (or molecule) circumference.

non-linearity: The property of a CCD’s readouts (ADU counts) failing to be proportional to the accumulated number of photoelectrons within a pixel when the number of photoelectrons exceeds a “linear full well capacity.” See also “linearity.”

occultation: Orbital motion of a larger object in front of a smaller one, possibly obscuring some of the light from the smaller object. c.f. transit.

OOT: Out-of-transit portions of a light curve. OOT data can used to assess the presence and magnitude of systematic errors produced by image rotation and color differences between the target star and reference stars.

photoelectron: Electron released from a CCD’s silicon crystal by absorption of a photon. One photon releases exactly one electron.

photometric sky: Weather conditions that are cloudless and calm (no more than a very light breeze), and no discernible haze due to dust.

photometry: Art of measuring the brightness of one star in relation to either another one or a standard set of stars (photometric standards, such as the Landolt stars). Brightness is often loosely defined, but in this case it can be thought of as meaning the rate of energy flow through a unit surface, normal to the direction to the star, caused by a flow of photons incident upon a telescope aperture. c.f. all-sky photometry.

photometry aperture and circles: A circular “signal aperture” within which a star to be measured is placed, specified by a radius [pixels], surrounded by a gap with a specified pixel width, surrounded by a sky background annulus. An aperture configuration is specified by 3 numbers (the 3 radii). Some photometry programs do not have a gap capability.

plate scale: Also referred to as “image scale,” is the conversion constant for pixels to ”arc on the sky. PS [”arc/pixel] = 206.265 × pixel width [nm] / EFL [mm]

point-spread-function, PSF: Shape of light intensity versus projected location on sky (or location on the CCD chip) by a point source (star), with widths described by FWHM and aspect ratio.

Poisson noise: Subset of stochastic noise pertaining to the case in which a discrete number of “random” events occur during a specified time originating from a “source” that is assumed to be at a constant level of activity during the measurement interval. The “Poisson process” is a mathematical treatment whose most relevant statement for photometry is that when a large number of events are measured, n, the SE uncertainty on the measured number is sqrt(n). cf. stochastic noise

precision: The internal consistency among measurements in an observing session. All such measurements may share systematic errors, which are unimportant for the task of detecting transit features. Precision is affected almost entirely by stochastic processes. Accuracy is different from precision; accuracy is the orthogonal sum of precision and estimated systematic errors.

Rayleigh scattering: Atmospheric molecular interactions with light waves that bend the path of the wave front and therefore change the direction of travel of the associated “photon.” This is what makes the sky blue. c.f. Mie scattering

read noise: The RMS noise produced by the process of reading a pixel’s accumulation of photoelectrons at completion of an exposure. Read noise [counts] = RMS’ / sqrt(2), where RMS’ is the counts “standard deviation” for an image produced by subtracting two bias frames. Read noise for modern CCDs is so small that it can usually be neglected when assessing error budgets. c.f. Appendix F.

reference star: A star in the same image as the target star and check stars whose flux is used to form ratios with the target and check stars for determining magnitude differences. The purpose can be detection of image to image changes or simply an average difference between a calibrated star and an uncalibrated or variable star. This is called differential photometry when the reference star is another star. When several reference stars are used it is called “ensemble photometry.” When the reference star is an artificial star it is a special case of differential photometry (without a name, as far as I know). The term “comparison star(s)” is sometimes confused with reference star(s); this is a term left over from the days when visual observers of variable stars used stars of similar magnitude to “compare” with the target star.

residual image: When photoelectrons remain in the silicon CCD elements after a read-out they may be included in the next exposure’s read-out and can produce a faint residual “ghost image” from the earlier image. This is more likely to occur after a long exposure when bright stars are present that saturate some CCD elements, causing photoelectrons to become more firmly attached to silicon impurities than other electrons. The problem is most noticeable when the following image is a dark frame; the problem is worse when the CCD is very cold.

saturation: Saturation can refer to a pixel’s output exceeding it’s “linear full well capacity” with an associated loss of proportionality between incident flux and CCD counts. The ADU counts where this proportionality is lost is the linearity limit (typically ~40,000 to 60,000 counts). Saturation can also refer to the accumulation of so many photoelectrons that the analog-to-digital converter (A/D converter) exceeds its capacity for representing an output value. For a 16-bit A/D converter this version of saturation produces an ADU count of 65,535.

SBIG: Santa Barbara Instruments Group, located in Goleta, CA (west of Santa Barbara; formerly located in up-scale Montecito, east of Santa Barbara; and never located in Santa Barbara).

scintillation: Intensity fluctuations of stars observed from the ground (caused by atmospheric temperature inhomogeneities at the tropopause). Scintillation can vary by large amounts on minute time scales (doubling), but time-average fluctuation levels are fairly predictable using dependencies on air mass, site altitude, telescope aperture, wavelength and exposure time.

sky background level: Average counts within the sky background annulus. Dark current is one contributor to background level, and it increases with CCD temperature, doubling every ~4 degrees Centigrade. Sky brightness is another contributor. A full moon will raise sky brightness from ~21 magnitude per square ”arc to 17 or 18 magnitude square ”arc. The increase is more than 3 or 4 magnitudes in B-band, which is the motivation for using a BB-filter when moon light is present.

SNR: signal-to-noise ratio, the ratio of measured “flux” to SE uncertainty of that flux. For bright stars SNR is affected by Poisson noise and scintillation, whereas for faint ones the dominant components are thermal noise generated by the CCD silicon crystals (“dark current”), electronic readout noise and sky background brightness. SNR [mmag] = 1086 * SNR.

star color: Difference in magnitude between a wavelength band and a longer one, such as B-V, V-R, or J-K. They are correlated with each other for most stars.

stochastic error: Uncertainty due to the measurement of something that is the result of physical events that are too numerous and impractical to calculate (thermal noise) or beyond present knowledge too understand because the physics of it hasn’t been discovered (radioactive emissions), which nevertheless obey mathematical laws describing the distribution of events per unit time. These mathematical laws allow for the calculation of noise levels, or uncertainty for a specific measurement. c.f. Poisson noise. Stochastic errors are different from systematic errors in that stochastic SE can be reduced by taking more measurements with the expectation that after N measurements SE = SEi / sqrt (N) (where SEi is the SE of an individual measurement). Systematic errors are unaffected by more measurements.

stray light: Light that does not follow the designed (desired) optical path, as happens with reflection of light from nearby bright stars (or moonlight) off internal structures, which is registered by the CCD. Light that leaks through a housing joint (CCD, or CFW, or AO-7, etc) and is reflected onto the CCD is stray light.

sub-frame: Rectangular area of CCD, specified by the user, that is downloaded when fast downloads of a smaller FOV are desired.

TheSky/Six: A good sky map program (also referred to as a “planetarium program”) showing star locations for any site location, any date and time, and any orientation (zenith up, north up, etc). J, H and K magnitudes are shown for virtually every star shown (plus V-magnitude estimates). Limiting magnitude is ~16 (V-mag). User objects and telescope FOVs can be added to the catalog.

transit: Orbital motion of a smaller object in front of a star that is larger, obscuring some of the light from the star. c.f. occultation.

transit depth: Magnitude difference between the measured value at mid-transit and a model-predicted value at the same time. In the absence of systematic errors affecting the shape of the light curve (which often have a component of curvature correlated with air mass and a trend correlated with time) the transit depth is simply the difference between the average of the out-of-transit magnitudes and the mid-transit value, which is what most observers do even when systematic effects are present (unfortunately).

transit timing analysis: Search for patterns in a plot of mid-transit time minus predicted transit time versus date using a fixed period (interval between transits). Anomalies that persist for months before changing sign, with sign reversal periods of many months, are predicted to occur if an Earth-mass exoplanet is present in an orbit whose period is in a simple resonance with the transiting exoplanet’s period (such as 2:1).