XO1b

DERIVATION OF XO-1b PLANET SIZE

Bruce L. Gary (GBL), Hereford Arizona Observatory (G95)

This web page is my amateur attempt to derive a planet size from an exoplanet transit light curve.

My plan for determining the planet size is to:
    1) adopt one (simple) limb darkeing model,
    2) calculate transit duration versus center-miss-distance for some approximately-correct planet size,
    3) use the measured transit duration to determine a center-miss-distance,
    4) calculate transit depth versus center-miss-distance, and
    5) adjust the planet size to agree with the measured transit depth.

Next I'll change the limb darkening model and repeat the above. One of these two limb darkening assumptions will provide a better match to the observed shape of the transit. This will allow for a crude estimate of which limb darkening model is correct, and also allow for planet size uncertainty to be estimated based on limb darkening uncertainty.

I use a spreadsheet with 2810 cells representing the star's solid angle (I actually use 1/2 this number to represent a half-disk). Each cell is assigned a "brightness" using the adopted limb darkening model. The limb darkening model is based on a table in Allen's Astrophysical Quantities (Second Edition), page 170, listing relative solar brightness for a selection of wavelengths and sine(theta) values.

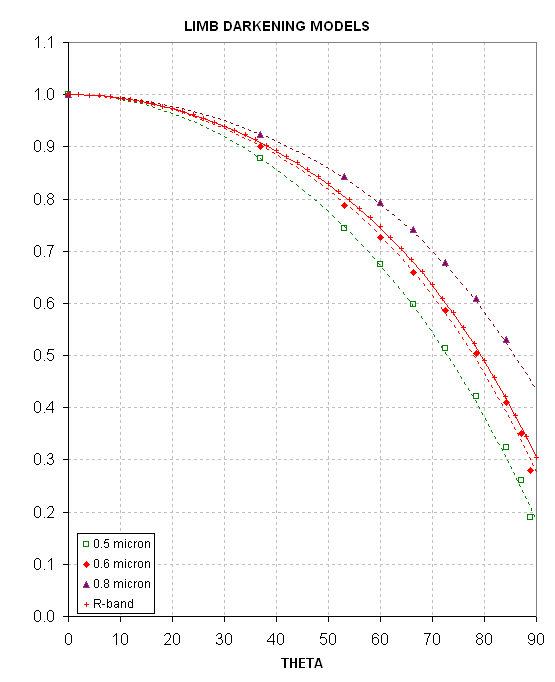
Figure 1. Limb darkening modesl for the sun at 4 wavelengths, including that for a typical R-band filter (0.63 microns).

The following analysis adopts the the R-band limb darkening model depicted in this figure.

My first estimate for the planet's solid angle is to use 61 cells in an approximately circular pattern. These are "moved" across the star disk at various row values (corresponding to various center-miss-distances). The next figure shows the unblocked brightness versus planet location (star radius units) for several center-miss-distances.

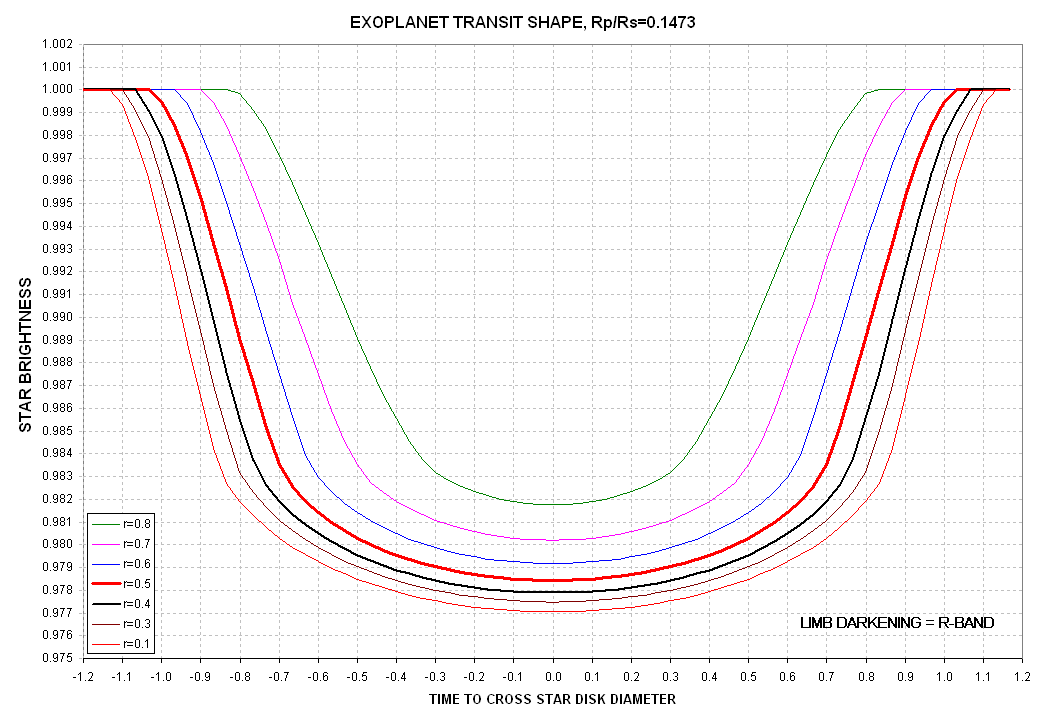
Figure 2. Shape of transits for Rp/Rs = 0.1473 and R-band limb darkening model.

This graph can be read to produce a table of "half depth transit duration" versus center-miss-distance. This is shown with a model fit in the next figure.

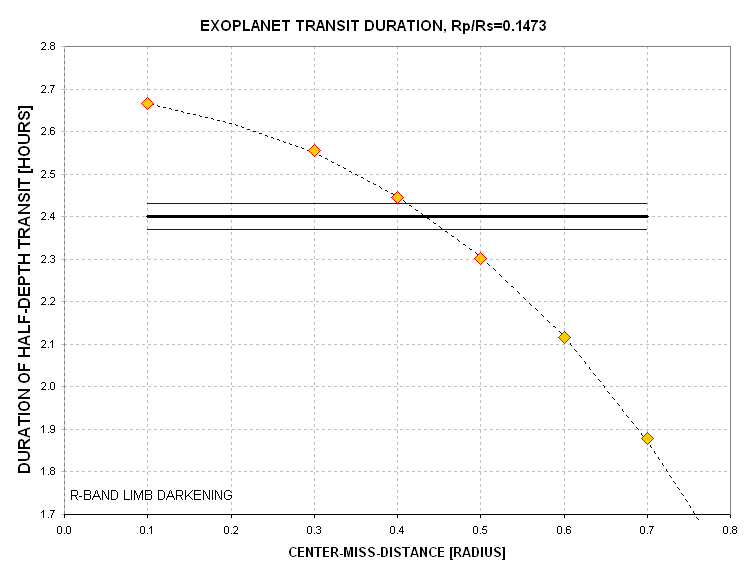
Figure 3. Half-depth duration versus center miss distance for adopted limb darkening and Rp/Rs = 0.1473 (obtained by measuring previous graph). The horizontal lines correspond to my 2006.03.14 measurement of the "half-depth transit duration."

Based on this graph I determine that the center-miss-distance is 0.433 +/- 0.022 star radii.

The next figure shows transit depth versus center-miss-distance for the assumed planet size.

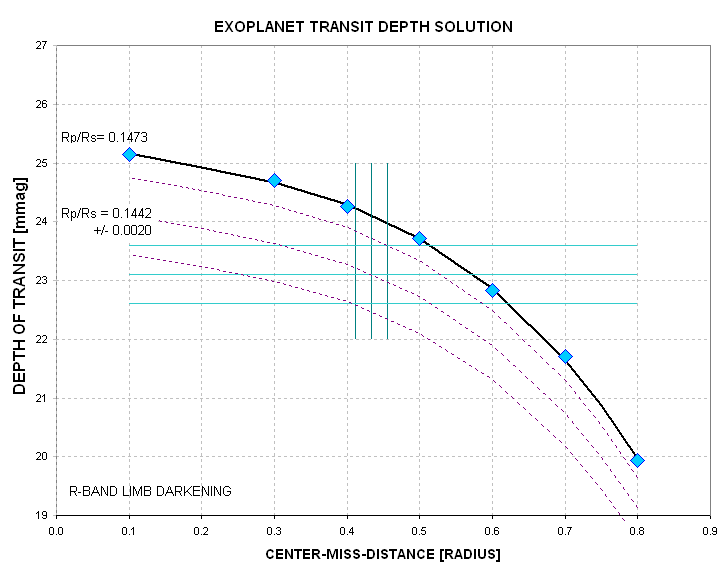
Figure 4. Depth versus center-miss-distance for Rp/Rs = 0.1473 (top curve) and 0.1442 +/- 0.0020 (lower curves).

For a center-miss-distance of 0.433 star radius the transit depth is ~24.1 mmag. We need a smaller planet size to match the observed transit depth of 23.1 +/- 0.5 mmag. Since solid angle varies as the square-root of radius, we need to decrease the radius using a factor sqrt(23.1/24.1) = 0.979. The new planet radius is Rp/Rs = 0.1442 +/- 0.0020.

Note that I'm assuming that if I were to decrease the planet radius by 2% the transit shapes versus center-miss-distance would not change significantly. This is OK to first-order because the shapes are mostly determined by miss distance and limb darkening. Therefore, Fig.2 should not be sensitive to the slightly too-small planet size. And this means that I can increase planet size to achieve a transit depth match without having to re-size the spreadsheet cells.

Let's convert Rp/Rs to Rp/Rj. Jupiter has an equatorial radius Re = 6.2 % greater than its polar radius whereas the sun is circular. The radius corresponding to the same solid angle as Jupiter is sqrt(Re*Rp) = sqrt(1-0.062) = 0.9685 * Re. Relating this to solar radius units, Rj/Rs = 0.9685 * 71492 / 695980 = 0.099486. Converting Rp/Rs to Rp/Rj using this ratio gives Rp/Rj = Rp/Rs * Rs/Rj:

Rp/Rj = 1.45 +/- 0.020

where the SE is subject to an additional increase due to the unjustified adoption of one limb darkening model.

Here's how this model fits my 2006.03.14 observations.

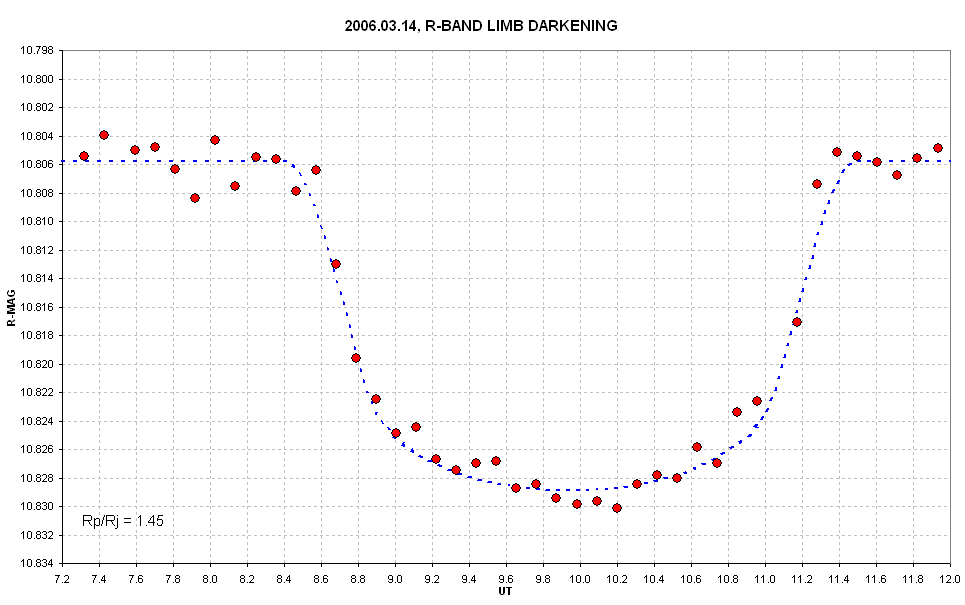
Figure 5. Observed and model fit using Rp/Rj = 1.45 and limb darkening corresponding to R-band.

To assess the sensitivity of the limb darkening assumption the previous analysis was repeated using I(theta)/I(0) = 1 - 0.60 * (1-cos(theta)), as shown in the next figure.

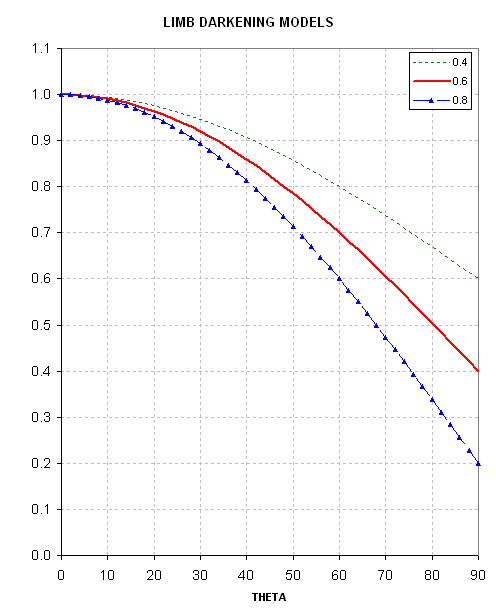
Figure 6. Three simple limb darkening models. The middle one, with constant 0.60, was used to produce the next graph.

The Rp solution was Rp/Rj = 1.44 +/- 0.02, and the model transit light curve is shown in the next figure.

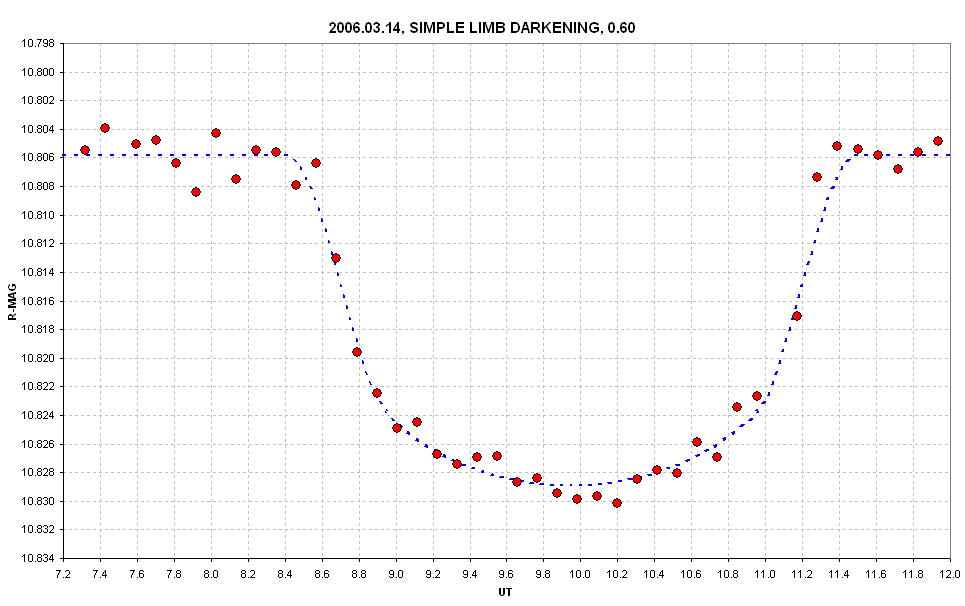
Figure 7. Observed and model fit using Rp/Rj = 1.44 and simple linear limb darkening model with a "1-cos(theta)" coefficient of 0.60.

This is a better-fitting light curve model and it might suggest that the simpler limb darkening function is a better approximation to that for the star XO-1a.

____________________________________________________________________

This site opened: March 28, 2006. Last Update: March 29, 2006