Rockwell MTP tutorial Note: The following is the original version of the tutorial prepared in 1991 for Rockwell International's Collins Air Transport Division. Nothing has been changed from the original. A version with a different "tempo" can be found at http://brucegary.net/MTP_tutorial/x.htm. The version here is faster-paced and provides more information, but in some ways it is dated. The other version may be better as an introduction because it explains more of the underlying concepts; it has the style of a "MTP for Dummies" and maybe it should be consulted whenever a concept in this version is not explained.

If the text of this web page is too small, you may enlarge it by clicking on your browser's View menu, Text Size, Increase.


     TUTORIAL ON AIRBORNE RADIOMETERS

       FOR AVIATION SAFETY APPLICATIONS

 

                                                                                 1991 May 19

 

                                                                                    Bruce L. Gary

                                                                                6233 Cloverly Ave

                                                                            Temple City, CA 91780

INTRODUCTION

 

This "tutorial" is written for those employees of Rockwell International (especially the Collins Air Transport Division) who want a general understanding of how microwave radiometry works, and how instruments employing this technology can provide information useful to pilots.

 

Microwave radiometer instruments are potentially useful in the following three areas:

 

1) Low Altitude Wind Shear (LAWS),

2) Clear Air Turbulence (CAT), and

3) Flight level selection for fuel savings.

 

Since infrared technologies are also potentially useful for the LAWS and CAT applications, I will occasionally highlight significant differences of the two technologies for these two applications.

 

Measurement concepts for microwave radiometers are explained in sufficient detail to enable the reader to compute observed quantities for simple cases not explicitly treated in the text.  This has been done at the risk of boring the "executive" reader, so I have tried to indicate which sections can be skipped without losing the "flavor" of what microwaves are good for.  The executive reader is now invited to scan the next two major sections and then begin reading the sub-section "Altitude Temperature Profiles."

 

THERMAL RADIATION FUNDAMENTALS

 

Microwave photons, like all photons, interact with all matter, whether the matter is solid, liquid, gaseous or plasma.  The term "interaction" means that a photon can be absorbed by the matter, reflected by it, refracted by it (after entry into it).  Photons can also be emitted by matter.  Emitted photons are called "thermal radiation" (therea re a few minor exceptions, such as synchrotron radiation, masers and lasers, etc., which are called non-thermal radiation).

 

The probability of an interaction of a photon with matter depends on the wavelength of the photon and the matter in question.  There is a maximum rate which a "simple" material (at uniform temperature throughout) can emit "thermal" photons per wavelength interval.  A material emitting photons at this maximum rate (at each wavelength) is said to be a "blackbody." 

 

Blackbodies emit photons across the wavelength spectrum with predictable energy output per wavelength interval given by the famous Planck Equation.  For long wavelengths the emitted energy is proportional to the temperature of the material.  For short wavelengths the emitted energy is strongly dependent on temperature. 

 

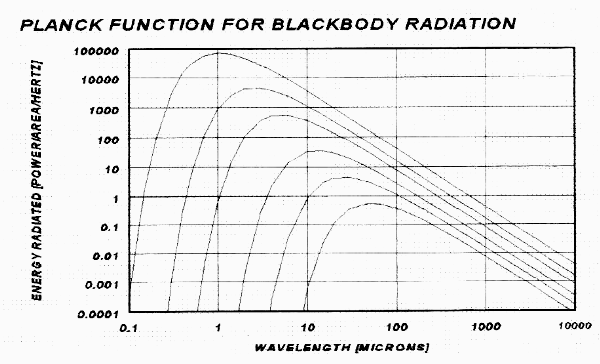
Fig 1 Blackbody spectrae

Figure 1. Planck Equation showing radiation intensity versus wavelength for the temperatures 100, 200, 400, 1000, 2000, and 5000 K. Power radiated is in relative units.


For objects at everyday temperatures microwaves are "long."  For these objects the emitted energy is proportional to temperature, provided the wavelength is much longer than about 4 microns.  For most infrared radiometers (8-14 microns, for example) the energy per unit wavelength interval varies in a more complicated way with temperature.  At wavelengths shorter than about 4 microns the emitted thermal radiation is so weak that it is easily overwhelmed by even small amounts of reflected sunlight, street lights, etc. 

 

A microwave radiometer is simply a device whose output is related in a linear manner to the number of photons emitted by the material being "viewed."  Since a doubling of the flux of photons is produced by a doubling of the physical temperature (Kelvin temperature) of the material, the radiometer provides a simple means for measuring the physical temperature of the material.  Since this measurement can be made from a distance from the object, a microwave radiometer is a remote sensor for measuring an object's physical temperature.

 

All materials absorb photons with some finite probability per photon.  Liquids and solids generally have properties that vary slowly with wavelength, although some minerals have resonance features at specific wavelengths.  Molecules in a gaseous medium that absorb photons may move their electrons to higher shells (possibly becoming ionized), they may vibrate more, or they may rotate faster.  All these changes are "quantized."  The energy quantization for molecular rotation is smaller than for the other changes.  Thus, long wavelength photons are capable of changing molecular rotation. 

 

ATMOSPHERIC ABSORBERS/SCATTERERS

 

The following sub-sections survey atmospheric constituents that either absorb or scatter at frequencies near 60 GHz and wavelengths in the 8 to 40 micron region.  The next major section discusses how to use this absorber/scatterer information to calculate observed microwave brightness temperature for hypothetical atmospheres, and how to do the reverse - to convert measured brightness temperature to desired atmospheric properties.  Some readers may want to merely browse through the following sub-sections and give more attention to the next major section.

 

Oxygen

 

Oxygen molecules have quantized rotations corresponding to the energy carried by microwave photons with wavelengths of approximately 5 millimeters (frequencies of about 60 GHz).  Several dozen of these quantized states exist within the frequency interval 48 to 71 GHz (one exists at 119 GHz).  At sea level the atmospheric pressure is so high that collisions between the molecules distort them enough to "smear" the spectrum of interaction probability versus frequency.  Thus, at sea level the absorption coefficient of oxygen versus frequency is a smooth function throughout the 50 to 70 GHz region.  At higher altitudes there is less "smearing," and the individual resonance absorption lines can be easily discerned.  This is the so-called resonant absorption spectrum of oxygen in the microwave region (see Fig. 2).


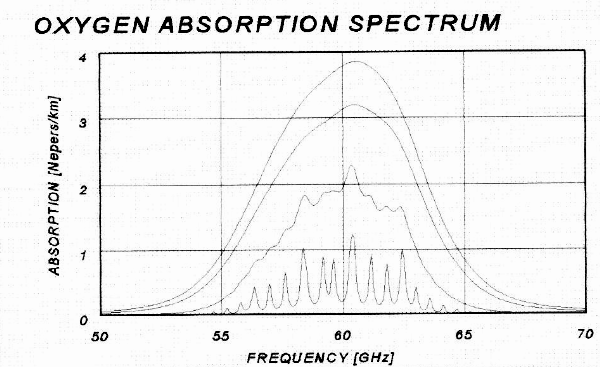
Fig 02


Figure 2. Absorption spectrum of oxygen for altitudes 0, 2, 10 and 20 km.


Absorption coefficient, Kv, is given in units of [Nepers/km] in this tutorial.  To convert to [db/km] multiply the [Nepers/km] value by 4.343.  In a medium where Kv = 1 [Nepers/km] a photon will have a 1/e = 0.37 probability of being transmitted (and a 1 - 1/e = 0.73 probability of being absorbed) after traversing 1 km within the medium.

 

Carbon Dioxide

 

Carbon dioxide does not absorb below frequencies of 115 GHz, so it is of no concern to microwave radiometers operating in the 60 GHz region.

 

In the IR there are strong absorption bands, such as at 14 to 16 microns.  Since CO2 is a well-mixed atmospheric gas, and since its absorption properties are known, it is possible to predict CO2 absorption at all altitudes.  This CO2 IR absorbing feature is similar to the 60 GHz O2 microwave absorbing feature in the sense that both wavelength regions can be used for remotely sensing the temperature of the atmosphere.  However, since some of the individual lines in the 14 to 16 micron region are very temperature sensitive care must be taken in calculating a predicted temperature sensitivity that matches the specific IR radiometer's passband.

 

Water Vapor

 

Water vapor has resonant absorption features as well as a non-resonant component.  Two significant water vapor resonances occur at 22.2 and 183 GHz.  The shape of the total water vapor absorption spectrum for the 10 to 70 GHz region is presented in Figure 3.




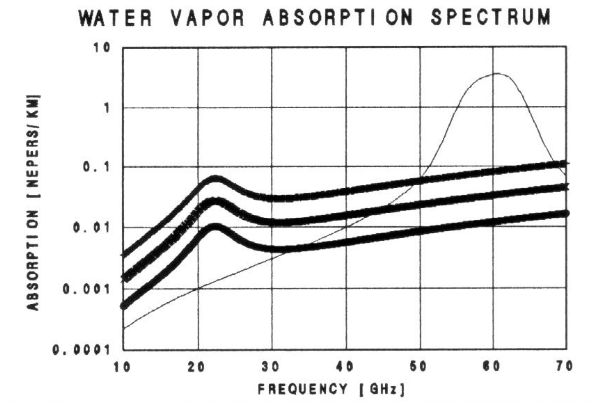
Figure 3. Water vapor absorption spectrum for typical surface conditions: air temperature = 15 C, RH = 15, 40 and 95% (1.9, 5.2 and 12.3 [g/m3]).  Note absorption spectrum for oxygen.


In the region 50 to 70 GHz water vapor is less absorbing than oxygen.  Water vapor concentration decreases rapidly with altitude (since temperature decreases with altitude and the saturation vapor pressure decreases with temperature).  The scale height for water vapor is approximately 2 km, instead of the 8 km for the well-mixed gases (nitrogen, oxygen, etc.).  Above approximately 10,000 feet it is possible to neglect the effect of water vapor for radiometers operating in the oxygen absorption region (50 to 70 GHz).  It is even possible to neglect the effect of water vapor at low altitudes in the middle of the 60 GHz oxygen absorption complex, except under warm and humid conditions.

 

IR photons are affected by water vapor if they are close to water vapor resonance absorptions lines.  The strongest IR absorbing features are at 5 to 8 and 19 to 300 microns.

 

Cloud Liquid Water

 

Liquid water droplets (ie, all clouds except cold cirrus) can be important absorbers for microwave radiometers.  They do not have resonant absorption features, but the non-resonant absorption increases with the square of frequency (throughout most of the microwave region).  Figure 4 shows the liquid water absorption spectrum for three cloud water concentrations.

 

To illustrate the effect of low altitude clouds on microwave measurements, consider a stratus cloud that is on the verge of drizzling.  It will have a liquid burden of about 700 microns and a thickness of approximately 0.7 km.  This corresponds to a Liquid Water Content, LWC = 1 [gm/m2].  The absorption coefficient of such a cloud in the 50 to 70 GHz region is 0.5 [Nepers/km].  This is comparable to levels sea level oxygen absorption values, which are 0.1 to 4 [Nepers/km].  There are some situations in which it is not necessary to take this into account (ie, when measuring lapse rates at flight level), and other situations in which it is necessary (ie, measuring horizontal temperature gradients at large distances).




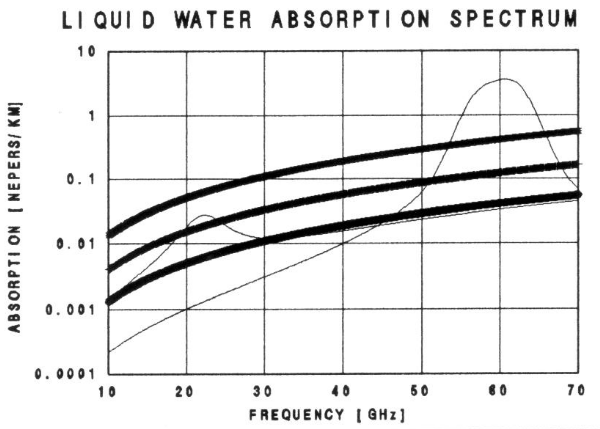
Figure 4. Liquid water (droplet) absorption spectrum for LWC = 0.1, 0.3 and 1.0 [gm/m3]. Absorption spectrum for oxygen (at sea level) and water vapor (40% RH at 15 C) are also shown.

For cumulus clouds, with LWC » 0.1 [gm/m2], Kv due to liquid water » 0.05 [Nepers/km].  This is small but not negligible compared with oxygen absorption, and the same comments in the last paragraph apply here.

 

At cruise flight levels LWC is even lower, and microwave absorption coefficients are correspondingly lower for a given temperature.  It should be noted that liquid water's absorption coefficient increases as temperature decreases.  Kv increases approximately 28% per 10 K temperature decrease.  Thus, a cloud with LWC » 0.1 [gm/m3] has Kv » 0.076 [Nepers/km] at -10 C instead of 0.046 [Nepers/km] at +10 C. 

 

Cloud droplets scatter, but near 60 GHz the scattering is insignificant compared to absorption.  Infrared photons, due to their shorter wavelength, experience (Mie) scattering that is far greater than the low levels of (Raleigh) scattering experienced by microwaves.  Absorption can also be significant, depending on infrared wavelength.

 

Rain

 

Rain drops are large enough to cause scattering losses that can be a few tens of % of the raindrop absorption at 60 GHz for large rain drops.  Nevertheless, absorption is still the more important effect, and for most situations scattering can be ignored.

 

Since infrared wavelengths are short compared with raindrop sizes they are scattered at significant levels.  IR radiation is also highly absorbed within rain.  {?? more info needed here ??}

 

Ice Absorption

 

Water ice is essentially transparent to microwave photons.  I have calculated that a typical cirrus cloud must be 400 km deep to provide an optical depth of 1 at 60 GHz (ie, Kv » 0.0025 Nepers/km).  This is 2 to 3 orders of magnitude less than oxygen absorption (at cirrus altitudes).

 

IR photons are both scattered and absorbed by ice crystals, though absorption is usually greater.  Many cirrus clouds are optically thick at IR wavelengths, which can lead to strong radiative cooling at their tops (due to loss of energy by radiation of IR photons to cold space) and strong radiative warming at their bottoms (due to absorption of earth surface IR thermal radiation).  IR remote sensing is probably hopeless while flying through cirrus clouds!

  

Aerosols

 

Non-water aerosols consist of dust and smog (at low altitudes) and condensation nuclei, polar stratospheric clouds and volcanic ash (at high altitudes).  All of these aerosol types produce negligible absorption and scattering of microwaves.

 

For example, a dust storm which obscures visible light at the rate of "one optical depth per 500 meters," which would cause an e-folding loss of visual signal every 500 meters, exhibits an absorption at 60 GHz of 0.3 % per 500 meters (I assume 100 micron diameter dust particles).  This is negligible, considering that oxygen absorption is 2 to 3 orders of magnitude greater.  By a similar argument it can be shown that high altitude condensation nuclei produce negligible absorption at 60 GHz. 

 

IR wavelengths are much smaller than the assumed dust grain size, so pure geometrical considerations show that the scattering loss will be 1 Neper per 500 meters, or 2 Nepers/km.  Absorption losses will also occur.  Therefore, interpretation of IR measurements will be ambiguous in dust storms (similar to the one in this example). 

 

Smog does not absorb appreciably in the microwave region.  From the perspective of the smog remote sensing community it would be good if smog did have absorption features, but none exist close to 60 GHz.

 

IR probably has smog absorption resonance features in the absorption spectrum (ie, NOx), but I do not know if smog absorbers are important for the endeavor of remotely sensing air temperature in the 15 micron region. {?? more info needed here ??}

 

Condensation nuclei (CN) at high altitudes are much smaller than IR wavelengths, so scattering will be comparable to molecular Raleigh scattering.  CN are not likely to pose a problem to IR sensors.

 

          Table I  Which Constituents Are Important?

Constituent       60 GHz     IR

 

Oxygen            Yes/No   Yes/No

CO2                No      Yes/No

Water Vap/surf    Yes/No   Yes/No

Water Vap/alt      No      Yes/No

Liquid Water      Yes(-)   Yes(+)

Ice (cirrus)       No      Yes/No

Dust Aerosols      No      Yes/No

PSC I              No       ?

PSC II             No      Yes

Volcanic Ash       No      No

Smog               No      Yes/No

Polar Stratospheric Clouds (PCSs) of Type I consist of nitric acid tri-hydrate particles approximately 1 or 2 microns in diameter.  They are found where temperatures are colder than about -78 C.  Such temperatures are not confined to the polar regions, as most people would think, but should be expected at equatorial latitudes near the tropopause.  Temperatures colder than  -83 C cause water vapor to condense onto the PSC Type I particles.  These Type II PSCs consist of particles with diameters 5 to 20 microns (leading eventually to "fall-out," or "dehydration").  I have calculated that PSC absorption by Type I and II PSCs is not detectable at 60 GHz.  Scattering should also be undetectable at 60 GHz.

 

I have not calculated how PSCs will affect IR radiation. It is possible that thick PSCs can increase IR absorption.  Scattering is not likely to be important for Type I PSCs, but could be significant for Type II. 

 

Volcanic ash at high altitudes is so tenuous, and the particulate is so small, that visible optical depth arguments should apply. Hence I do not think they will affect IR absorption characteristics. {?? more info needed ??}

 

The above table summarizes which components of the atmosphere are significant absorbers or scatterers for microwaves (near 60 GHz) and IR (8 to 40 microns). The entries "Yes/No" signify that only at some wavelengths does the constituent absorb/scatter significantly.  The (-) and (+) symbols denote "weakly" and "strongly".

 

REMOTE SENSING OF AIR TEMPERATURE

 

The previous major section surveyed atmospheric constituents that can produce absorption or scattering of microwave or IR photons. It was shown that for radiometers operating in the frequency interval 55 to 65 GHz oxygen molecules are the principle absorber, and as a first approximation the other atmospheric constituents can be ignored. The same cannot be said for IR radiometers, since the absorbing and scattering properties of so many constituents are potentially important. Under ideal conditions, however, IR radiometers can be treated like their microwave counterparts. 

 

I want to distinguish between two categories of useful things that both IR and microwave radiometers can do as atmospheric remote sensors:  1) column content measurements, and 2) air temperature at a distance.  I will briefly describe the first of these, then present a more detailed description of the second.

 

Column Content Measurements

 

At places in the IR and microwave spectrum where absorption coefficients are small it is possible to measure the column content of the principle absorber constituent. Water vapor and liquid water are the two most common examples. A microwave instrument that measures column content of water vapor and liquid water is called a Water Vapor Radiometer, or WVR. An example of an IR counterpart is the airborne instrument first used by Dr. Peter Kuhn on NASA's C-141 Kuiper Airborne Observatory. 

 

Referring to Fig. 3, at 22 GHz there is a water vapor emission feature with typical values for Kv » 0.027 [Nepers/km]. Combining this absorption value with an effective zenith path length of 2 km (a typical scale height for water vapor) yields a total absorption of 0.054 Nepers, or about 5.3%. The water vapor in the atmosphere will emit microwave radiation as if it were a blackbody (ie, opaque) at a physical temperature of 15 K (0.053 * 288).


But in this example the atmosphere is not opaque. An observer on the ground would not have enough information from the WVR measurement alone to distinguish between the following possibilities: 1) opaque at 15 K, 2) opaque at some higher physical temperature but emitting at less than unity emissivity (atmospheric molecular emission is at unit emissivity), or 3) partially transparent at a higher than 15 K temperature (the correct interpretation).

 

Of course, anyone knowing that the atmosphere could not be as cold as 15 K, and was in fact about 288 K and exhibits unit emissivity because it is a molecular emitter, would thereby know that the true condition was "partial transparency" of 5.3%. But considering this as one specific situation of a general class of situations, and acknowledging that it is not always possible to bring-in external information to resolve the ambiguity, it has been useful in the discipline of remote sensing of thermal emission to invent a term called brightness temperature. Thus:

 

Brightness temperature, TB, is simply the physical temperature required of an opaque material with unit emissivity to produce the measured intensity of photons.

1

Column contents can be deduced from TB measurements when the absorption coefficient of the radiating medium is known and when optical depth is small (ie, low values for the product of absorption coefficient and thickness).  In the example, knowing that TB = 15 K allows the WVR user to infer that there must be 1.04 [gm/m2] of water vapor overhead. This inference is based on the following logic (which the casual reader is free to skip):

 

  TB = Teff * (1 - e-τ)                                                                     (1)


     where Teff º "effective" temperature of radiating medium,

     τ (optical depth) = Kv * Δz, and

     where Kv = known function of vapor density, and

     Δz = effective thickness of water vapor layer

 

  Vapor Burden = ρvapor * Δz                                                       (2)

 

In this example TB = 15 K, Teff = 288 K, Kv = 0.027 * (vapor density)/(5.2 [g/m3]), which allows for the solution: τ = 0.0535, and vapor burden = 1.04 [g/cm2]. 

 

A similar reasoning is used to convert IR radiometer measurements of upward-looking brightness temperature to vapor burden, provided optical depth, τ, is small (which it was for Pete Kuhn's 20 micron IR radiometer, flown on the C-141 aircraft, at cruise flight levels). 

 

Ground-based microwave WVR instruments operate at 20.7 and 31.4 GHz, typically. The 20.7 GHz channel's intended use is to derive water vapor burden. The 31.4 GHz channel's intended use is to derive liquid water burden. Figure 4 shows that for LWC = 1.0 [g/m3], at 31.4 GHz Kv » 0.11 [Nepers/km]. By an argument similar to that given for deriving vapor burdens, it can be calculated that when TB = 21.3 K at 31.4 GHz, and Teff = 288, there is a liquid water burden of 0.07 [g/cm2]. (These values correspond to the 700 meter thick "drizzling stratus" cloud described in the "Liquid Water" section of the previous major section).  

 

Altitude Temperature Profiles

 

A radiometer that is immersed in an "infinitely" large absorbing/emitting medium which is at a uniform physical temperature Tm will produce a measured brightness temperature TB = Tm. If an antenna is attached to the radiometer, so that only photons from a restricted viewing direction influence the radiometer output, TB is unchanged.

 

Figure 5 depicts a "weighting function" that describes the relative contribution to the radiometer's output by emitting volume elements, as a function of distance of those volume elements along the viewing direction r that is inclined an angle θ above the horizon. The volume elements are defined such that they are bounded by a fixed solid angle and a fixed range increment. If there were no absorption between the volume element and the receiving antenna, and if each volume element were at the same physical temperature, the antenna would intercept the same number of photons per unit time from each volume element. 

 

Because there is absorption by intervening material, the weighting function W(r) decreases with range r. Provided the absorption coefficient, Kv, is constant with range, the weighting function has an exponential shape. W(r) is reduced to 1/e at a distance called the "applicable range," Ra. This means that where r = Ra, only 37% of the photons are able to reach the antenna, whereas at r = 0, all photons are able to reach the antenna.

 



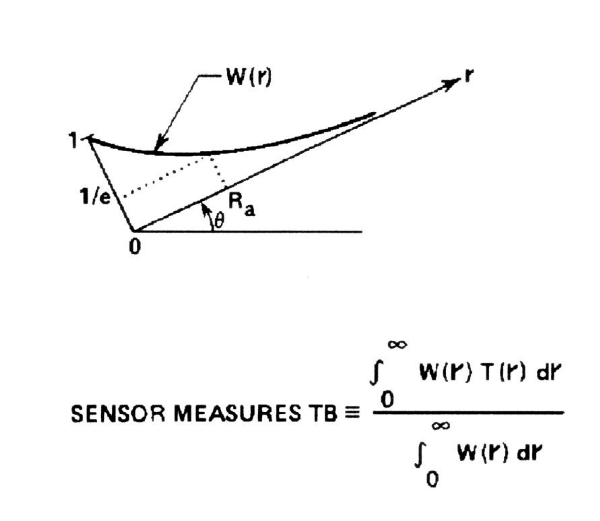
Figure 5. Brightness temperature measurement theory, for view along direction r inclined angle θ above horizon, showing weighting function W(r). At r = applicable range, Ra, W(r) = 0.37.


If the entire emitting region were to change temperature, TB would undergo a corresponding change. This is because each volume element would be emitting a fixed ratio of photons in relation to that for the original temperature.  But what happens if only some volume elements change temperature? 

 

The weighting function W(r) can be used to calculate the change in TB for a temperature change at any range increment. It is intuitively reasonable that the equation in Fig. 5 can be used to calculate TB. Note that the "source function" is T(r), and it is weighted by W(r) to yield an effective radiating temperature TB.

 

There is a useful property of exponential weighting functions which is extremely valuable in this situation:

 

When an exponential weighting function is applied to a linearly varying source function, the weighted result equals the value of the source function at the location where the weighting function = 1/e.

2

In other words, if temperature varies linearly with range (ie, if T(r) is a linear function along the viewing direction), and if the Kv of the medium is constant along the viewing direction, then TB = T(Ra)! 

 

Now consider the case in which the temperature field is horizontally stratified.  It becomes possible to transform from the range coordinate to a height coordinate, according to:  h = r * sin(θ). This leads to the concept of an "applicable height" which varies with θ:

 

                                Ha = Ra * sin(θ)

 

The source function is a linearly varying function of height, and the weighting function will vary exponentially with height if Kv is constant with height, so it is possible to state that:

 

When air temperature varies linearly with altitude along the viewing direction, and when absorption coefficient is constant along the viewing direction, then T(h) can be derived from TB(θ) by using the equivalence:   h = Ra * sin(θ). 

3

When the stated conditions exist, it is possible to derive a profile of air temperature with altitude by measuring TB(θ), provided a value for Ra can be determined.  The procedure is to first derive TB(θ), then replot TB versus Ra * sin(θ) and rename the plot as T(h).

 

Ra is simply 1/Kv.  Since Kv in the 60 GHz region is a function of frequency, pressure and temperature in the atmosphere (to first order), Ra can be calculated from easily measured atmospheric parameters.  For example, referring to Fig. 2, while flying at 10 km and operating a 60 GHz radiometer, Kv » 2.0 [Nepers/km].  Thus, Ra » 0.5 km.  If the antenna is pointed through a range of elevation angles from -90 to +90 degrees, it should be possible to estimate air temperature over an altitude range of 1.0 km (from 9.5 km to 10.5 km).

 

The remote sensing capability just described assumes that T(z) is linear over an altitude region of unspecified extent; and it assumes that Kv changes by only a small amount across the same altitude region.  We will return to these assumptions, as well as others not yet stated.  For now, however, it will be instructive to pursue the power of such a simple radiometer operated in an elevation scanning mode, with its TB output subjected to such a simple analysis algorithm.

 

In describing something complex it is sometimes useful to employ a series of explanations that begin with a very over-simplified picture, which can be replaced with more and more accurate representations later.  Thus, I invite the reader to begin by thinking of a microwave radiometer operating in the 60 GHz region, and mounted on an aircraft, as similar to a long stick with a thermometer on the end that is waved up and down in front of the aircraft.  Figure 6 conveys this idea.

 



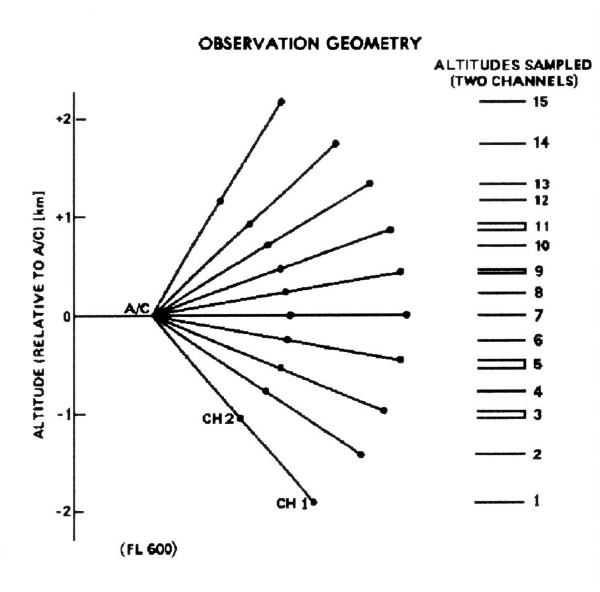
Figure 6. Microwave Temperature Profiler's viewing geometry, showing where air temperature measurements are "made" during each scan of 10 elevation angles.


This figure is for the JPL Microwave Temperature Profiler, MTP, which is mounted in NASA's ER-2 aircraft, also referred to as MTP/ER2.  MTP/ER2 operates at two frequencies, 57.3 and 58.8 GHz, called "channel 1" and "channel 2." When flying at 60,000 feet altitude the applicable ranges for these channels are Ra = 2.5 and 1.5 km.  In the Fig. 6 the "stick with a thermometer at the end" has these lengths, and it sweeps through a set of 10 elevation angles during each scan. The "dots" in the figure denote the "applicable locations" for each of the elevations, for each channel. (On the right is shown how the redundant observables are combined into a set of 15 "independent" observables.) 

 

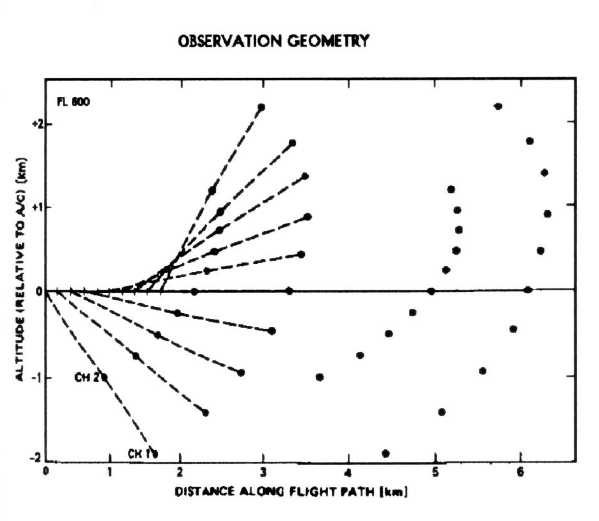
This "starting point" simplification is made slightly more realistic in Fig. 7, where aircraft motion through the air is taken into account. The ER-2 flies at Mach 0.7, or 210 [m/s]. Each MTP scan (presently) requires 14 seconds to complete.  During this 14 seconds the ER-2 moves forward 2.9 km as the scan proceeds from below the horizon to above. Two successive scans are shown, which are offset 2.9 km from each other. MTP sweeps-out a set of sampling points in a "curtain" cross-section that is approximately 4 km tall (while flying at 60,000 feet). 


 


Figure 7. Location of MTP air temperature sample locations after allowance for A/C motion.

The next increment of realism to add to this picture is to explicitly acknowledge that Kv is not constant along the entire length of the viewing direction. It only needs to be constant for a distance of a couple Ra lengths in order to assume that the weighting function is approximately exponential. Slight departures from the exponential shape for the weighting function can be handled by calculating the exact shape of the weighting function directly, according to (note use of "z" instead of "h" to denote height):

 

                W(z) = e-τ μ * Kv(z) * dz                                                                                (3)

                   where τ = μ Integral [ Kv(z) * dz ]

                   and where μ = 1/sin(θ)

 

and then using this weighting function to calculate applicable height:

 

                Ha =  Integral [ z * W(z) * dz ] /  Integral [ W(z) * dz]                              (4)

 

This will provide an improvement over the assumption that Kv = constant throughout (which would produce an exponential weighting function, which in turn would have permitted the use of the simpler expression Ha = sin(θ)/Kv).

 

The next incremental improvement is to correct for any "transparency" that may exist. A transparency correction is needed for only those situations where the weighting function is "long" and the viewing direction is at least a few tens of degrees above the horizon. This may occur while flying at a high altitude and observing at frequencies well off the 60 GHz absorption peak. If the atmosphere is not completely opaque along the viewing direction then TB will consist of two parts:  an atmosphere part and a cold space "cosmic background" part. For example, suppose the atmosphere was 1% transmissive, and suppose the atmosphere were at a uniform temperature of 260 K. Then TB would be 0.99 * 260 [K] + 0.01 * 2.7 [K], or TB = 257.4 [K].  (Note here that I've adopted 2.7 K for the cosmic background brightness temperature; there are subtle second order effects requiring that a slightly different value be used, which are not worth getting into here). When the atmosphere is not opaque TB can be slightly less than the physical temperature of the atmosphere, and a small transmissivity is then required. 

 

For MTP it is necessary to apply transparency corrections while flying above 60,000 feet, and then only to the TB measurements where the viewing directions exceed about 20 degrees above the horizon. Detailed calculations must be made for each of the observables, ie, for each channel, at each elevation angle, each altitude, and each air temperature (and lapse rate). This can take several weeks of a person's time, so there's an incentive to minimize the amount of transparency that must be applied (this entails carefully selecting local oscillator center frequency and IF passband shape to minimize the amount of RF response in the "wings" of the oxygen absorption spectrum.) It will probably always be the case that transparency corrections will only be needed during flight at high altitudes.


 


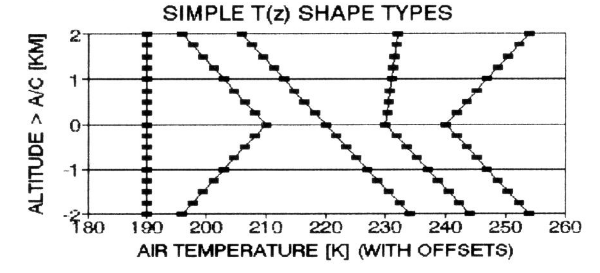
Figure 8. Altitude temperature profile shape types for which the "simple" procedure for converting TB(θ) to T(z) is fully adequate. The shape types are isothermal, IL top, featureless, tropopause, and IL base.


What about the assumption requiring that the source function, T(r), be linear with r? This requirement could be met by a variety of altitude temperature profiles, depicted in Fig. 8. But the five shape types depicted are special cases since the aircraft will not often be flying at the altitudes of temperature inflections, with deep layers having constant slopes for large altitude regions above and below flight level. Figure 9 illustrates two cases of inversion layer bases approximately 0.5 km above and below flight level.

 



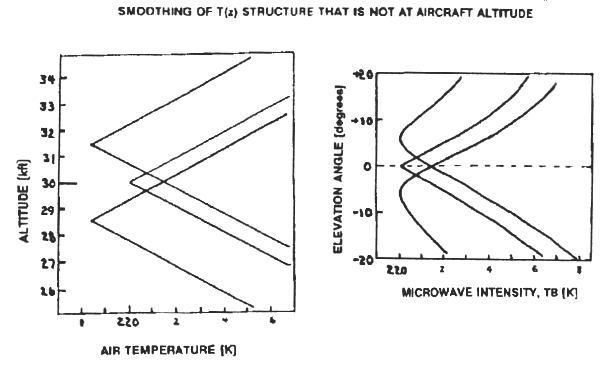
Figure 9. Examples of T(x) shapes with inflections displaced above and below aircraft altitude 0.5 km, for which the simple procedure for converting TB(θ) to T(z) is inadequate. Note the "smoothing" of observed TB(θ).


The "rounded" TB(θ) patterns in Fig. 9 show that the observed profile will underestimate the extremes of air temperature at the inflection altitude. All sharp inflections not close to flight level will be "rounded" and the altitudes of the inflections will be displaced toward the aircraft (by small amounts, not shown in this figure). This illustrates the major shortcoming of the simple procedure for converting observed TB(θ) to T(z). It should be noted, however, that measured lapse rate at flight level is least affected for these cases.

 

I believe that the details of the temperature structure near the inflection altitudes is less important than other aspects of the temperature profile, which are acceptably represented by the simple analysis procedure.  Usually the most important thing about such T(z) structures is the mere presence of the structure, and its altitude location in relation to the aircraft.  

 

Fig. 10, for example, shows a sequence of actual altitude temperature profiles based on MTP/ER2 data which has been reduced using the simple data analysis procedure. Altitude is resolved into rows 1100 feet apart (with the blank row representing the aircraft's altitude of 19.69 km), the horizontal temperature scale is resolved into 0.25 K columns, and each of the altitude temperature profile sequences is displaced 20 columns (5 K) to the right of its neighbor for clarity. The data were made while flying within an inversion layer. The lapse rate at flight level can be seen to vary, and the temperature contrast across the inversion layer also varies. For CAT warning objectives it can be argued that the most important pieces of information to be extracted from such a data set is that 1) the aircraft is flying in the middle of an inversion layer, 2) the lapse rate within the inversion layer is approximately +1.5 [K/km], 3) that the inversion layer is approximately 1.5 km thick, and 4) each of these properties is variable on a timescale of 14 seconds. This is a significant amount of information, and it is all reliably obtainable using the simple procedure for converting TB(θ) to T(z). 

 



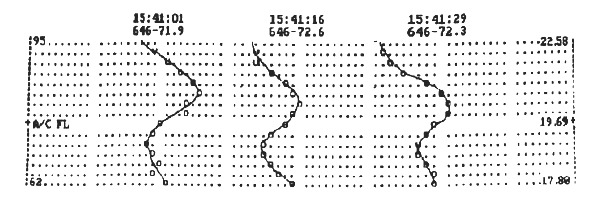
Figure 10. MTP measured "altitude temperature profiles" obtained using the simple procedure for converting TB(θ) to T(z). Each column represents 0.25 K, each row 1100 feet. Profiles are offset 20 columns. Note the changes in inversion layer properties.


Because the analysis procedures used for this data were "simple" it is not possible to believe the "softness" of the temperature inflections at the base and top of this inversion layer. Also, it is likely that the inversion base and top altitudes are slightly farther from the aircraft's flight level than implied by the observed profile. When such details are needed, the more rigorous approaches (described later) will have to be employed. So far, these more rigorous procedures (there are several) have just not been worth their trouble since they are significantly more laborious to set-up and use.

 

At this point in the description of how microwave observables are converted to altitude temperature profiles it is possible that "purist" readers will feel frustrated. The transformation from "observable space" to "reality parameter space" using the procedures described so far appear to lack rigor! This is true, and in a later section I will describe several more rigorous treatments. However, I want to state quite clearly that the simple procedure for converting observables to altitude temperature profiles works quite well! All of my published MTP results, for the ER-2 and all precursor instruments on other aircraft, are based on the procedures already described.

 

Air Temperature Horizontal Gradients

 

The previous sub-section describes how a 1-frequency radiometer can be scanned in elevation angle to produce observables that can be combined to yield an estimate of "altitude temperature profiles."  It was also shown how additional frequencies can be used to extend the altitude range of these profiles.  This sub-section describes how a horizontally-pointed radiometer can be used to estimate temperature along the viewing direction.  For this application it is necessary that more than one frequency be used.  When a sufficient sampling of frequencies are used it is theoretically possible to determine air temperature at several locations along the viewing direction, and by differencing them it is possible to infer the existence of horizontal temperature gradients.

 



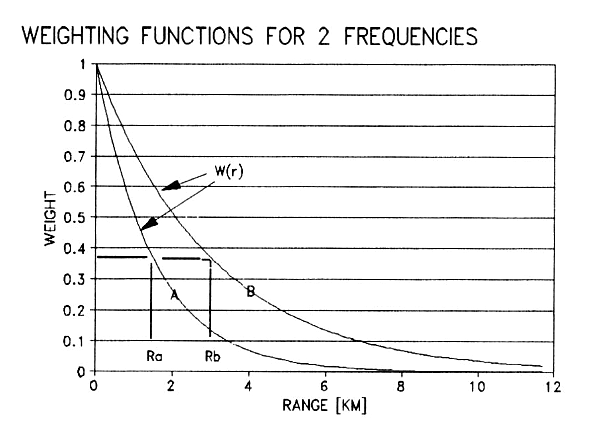
Figure 11. Weighting functions for 2 frequencies having applicable ranges of 1.5 and 3 km.

Figure 11 illustrates the situation when two frequencies are employed by a horizontally viewing radiometer.  Since air pressure is constant with range it can be assumed that Kv(r) is constant versus r, which means that the weighting functions have exponential shapes.  Channel A and B, in this illustration, have applicable ranges that differ by a factor of two.

 

The measured brightness temperatures for channels A and B, TA and TB, will be the weighted average air temperature corresponding to the weighting functions A and B.  If air temperature changes linearly with range then TA and TB will equal the air temperatures at the ranges Ra and Rb.  This affords a means for sensing the presence of a horizontal gradient of air temperature along the viewing direction.  In the above example, if air temperature varies linearly with range and is 5 K colder at r = Rb than at r = Ra, then the measured TB will be 5 K colder than TA.  An abrupt change of air temperature at a range of 3 km, for example, will produce a measured brightness temperature difference of about 3 K. 

 

The measured brightness temperature contrast is less than the true air temperature contrast.  The next sub-section describes ways of recovering some of this lost contrast.

 

Retrieval Concepts:  Backus-Gilbert

 

The difference between the weighting functions in Fig. 11 is called an "averaging kernel."  Figure 12 shows the averaging kernel Aba(r).  What is the "meaning" of this averaging kernel, and what is it good for? 

 



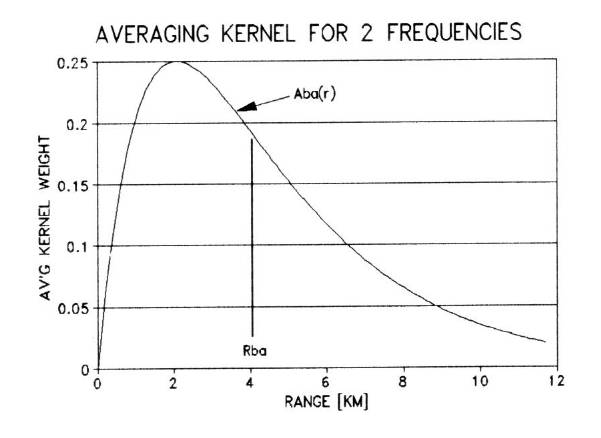
Figure 12. Averaging kernel derived from weighting functions in previous figure. Applicable range is 4.1 km.

If the areas under the weighting functions A and B are designated by α and β (after normalizing to produce unity at r = 0), then there is something special about the "artificially produced observable,"  TBA, defined by the following equation:

 



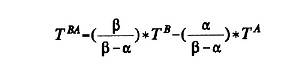
When the two Kv values are in the ratio 2 to 1, for example, then the areas under the weighting functions are in the ratio 1 to 2, and TBA = 2*TB - TA. The "artificially produced observable" TBA is a linear combination of the directly observed "observables" TA and TB. Note that the sum of the coefficients which "multiply" the directly observed observables add up to 1! (This is an obvious requirement, whose justification is left to the reader.)


With TBA defined this way it is intuitively clear that TBA is the brightness temperature that would be observed if a radiometer could somehow have the weighting function specified by the averaging kernel Aba(r). If a weighting function like Aba(r) could magically be created, then TBA would be the "directly observed observable." As it is, we must perform the magic manipulation ourselves by using TB and TA along with the proper coefficients to infer the TBA that would be measured. 

 

This manipulation to produce the equivalent of an "averaging kernel weighting function observable" is widely used under the name Backus-Gilbert retrieval to infer information about a source function's value at a narrowly defined range region. I will use the term "averaging kernel observable" to refer to this class of inferred "observed" quantity. The "applicable range" for the averaging kernel observable in Fig. 11 is simply the averaging kernel weighted range, Rba.  Note that the function Aba(r) "peaks" shortward of Rba. 

 

The multiplying coefficients used to convert the two observables TA and TB to the averaging kernel observable TBA are -1 and +2 in the above example. Their sum is +1. Other combinations that meet the "sum = 1" requirement can be used, but they will produce differently shaped averaging kernels. These differently shaped averaging kernels are not "wrong," they may simply not be "optimum." 

 

"Optimum" requires definition. Averaging kernels that are "bunched up" near their applicable range (Rba in the example) are more optimum than those which are "spread out." This subjective terminology can be made objective, but to do so would go beyond the scope of what is needed here.

 

It can be said that the 2-channel radiometer in the above example produces information about air temperature at three distances:  Ra, Rb, and Rba (in increasing distance). Other slightly different definitions of the averaging kernel do not contain sufficiently different information to constitute being considered new air temperature estimates.


The shape of the averaging kernel in Fig. 12 may be more "bunched up" near its applicable range compared with the weighting functions in Fig. 11, but there still is something unsatisfactory about the shape. It would be good if the averaging kernel shape were more impressively confined to a region near the applicable range. This is achievable, but more than 2 directly measured observables are required. 

 

There is a rule of thumb stating that "in the limit" the half-response points of an ideal averaging kernel are at distances of approximately 80% and 130% of the applicable range (provided the averaging kernel's applicable range is not near the ends of the set of weighting function applicable ranges). A sketch of an ideal, "in-the-limit" averaging kernel is shown in Fig. 13 using a thin line. 

 

A more realistic averaging kernel shape is also shown in Fig. 13, by the thick line. In this case the 8 observable applicable ranges are 1, 1.5, 2, 3, 5, 7, 10 and 15 km (note the approximate 1.5 ratio of the sequence). The multiplying coefficients used are +0.3, +7.9, -22.9, +21.5, -8.1, +4.6, -4.2 and +1.9. This alternating sign pattern is common, with large absolute values for the observables whose applicable ranges are close to the resultant averaging kernel's applicable range.

 



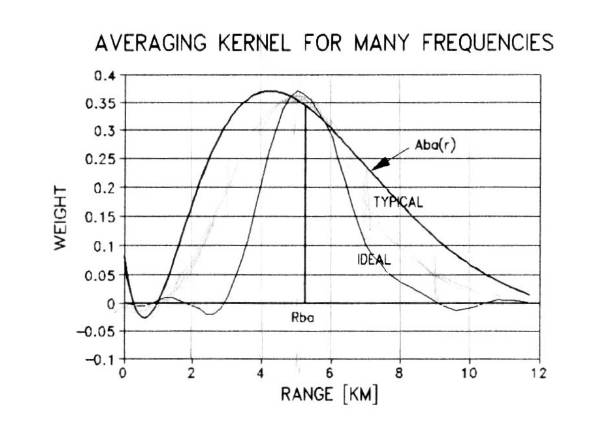
Figure 13. Improved averaging kernel using 8 frequencies (thick line) and "many" frequencies (thin line). Applicable range is 5.3 km in both cases.


For this specific set of 8 measured brightness temperatures it is possible to construct an averaging kernel having an applicable range of any value within the limits of the weighting function applicable ranges. The shapes degrade (i.e., begin to resemble the weighting functions) for applicable ranges at the near and far limits of this range region, and the best looking shapes are always in the middle. The samples in Fig. 13 are for the middle of the range of possible solutions.

 

Penalties are paid for achieving range discrimination using the averaging kernel concept. Observation noise is "amplified" since the averaging kernel observable is the result of taking the difference between two large numbers (the sum of the terms with positive coefficients minus the sum of terms with negative coefficients). In the case just described, with 8 terms, the averaging kernel observable can be expected to exhibit a stochastic uncertainty that is 34 times greater than for any of its constituent measured observables. If each measured observable has a noise uncertainty of 0.1 K, the averaging kernel noise uncertainty will be 3.4 K (for the 8-term case illustrated). 

 

Even more important than the amplification of stochastic noise is the amplification of calibration uncertainties. It is typical for the final absolute calibration of a radiometer to be uncertain by the amount 0.5 K. If each channel of an 8-channel radiometer were uncertain by this amount the 8-term averaging kernel solution would have an uncertainty of a whopping 17 K! It is forbidding to imagine how uncertain the "ideal" solution, with good range resolution, would be.  Clearly, there are trade-offs. And each radiometer system will require a tailored trade-off calculation that incorporates knowledge about expected absolute calibration error, stochastic errors, and the need for good range resolution.

 

There is a formalized procedure for handling the trade-offs of observable uncertainty and range resolution that produces coefficient sets that are optimum for any desired averaging kernel applicable range. I won't describe it here, because there's an even better procedure for obtaining optimum coefficients: the "statistical retrieval procedure" (to be described in the section after the next one).

 

Angle-Scanning Inter-Channel Calibration

 

Before describing the "statistical retrieval procedure" this would be a good place to digress to explain why angle scanning is better than frequency sampling. (The executive reader may want to skip this sub-section.)

 

The explanations in the previous sub-section (including Fig's 11 to 13) are for the "traditional" frequency sampling observing strategy. That is, each observed quantity comes from a separate radiometer channel. Most applications requiring the derivation of air temperature versus range have really been attempts to derive air temperature versus altitude from a ground station. Many observationalists have built radiometers with many channels which have been mounted in a zenith-fixed position. Such systems suffer the full impact of "calibration uncertainty amplification" when averaging kernel techniques are employed. (The same is also true when the "statistical retrieval procedure," to be described later, is employed.) 

 

Surfaces of equal temperature are amazingly flat. This fact can be taken advantage of by using a single channel radiometer to do the job of several frequencies by simply angle scanning, as is done for each channel of the MTP/ER2 instrument.

 

For example, I will describe a ground-based radiometer system called MARS, for Microwave Atmospheric Remote Sensor. MARS uses a 57.5 GHz radiometer to scan from zenith to 5 degrees above the horizon, making measurements at 7 elevations. Each of the 7 measurements produces a weighting function versus altitude (note the transformation from range to altitude) with an applicable altitude given by "applicable range times sine elevation." The applicable altitudes for MARS span the range 120 to 1400 feet. The observed quantities are indistinguishable from using a 7-channel radiometer pointed at zenith. But the angle scanning set of observables share the same absolute calibration uncertainty. Thus, they have a greater amount of "shape information," the shape of the curve of observed brightness temperature versus applicable altitude.  Consequently, the single-channel, angle scanning radiometer does a better job of sensing the presence of altitude temperature structure, and it is much less costly than a 7-channel counterpart.

 

Since the top altitude of 1400 feet is not high enough for most uses, two additional channels are included in MARS. They also angle scan, from zenith to 25 degrees elevation. Provided the frequencies and scanning angles are carefully chosen, as they were for MARS, such a hybrid angle scanning/frequency sampling radiometer system can be "self inter-calibrating." Specifically, the 57.5 GHz channel's zenith weighting function is identical to the 55.3 GHz channel's 25 degree elevation weighting function; and the 55.3 GHz channel's zenith weighting function is identical to the 53.9 GHz channel's 25 degree elevation weighting function. By this means each scan of the 3-channel assembly provides sufficient inter-calibration to allow data analysis to force all observables to share the same calibration. This procedure assures that the shape of the observables versus applicable altitude is correct, or unaffected by calibration uncertainties.

 

This hybrid radiometer system also provides a less costly way of providing a large dynamic range of applicable altitudes. The 3-channel MARS system measures brightness temperatures with 15 weighting functions having applicable altitudes that span the range 120 to 6900 feet. That's a dynamic range of almost 60 to 1! There is no way a zenith-fixed, multi-channel radiometer system can produce the same dynamic range, or the same quality of inter-channel calibration.

 

For the past 10 years I have promoted this observing strategy.  It has been demonstrated on numerous occasions using the MARS ground-based instrument, which is described further in a later section. We built an improved, much more compact version, for the Army. The same concepts can be used in airborne radiometers that endeavor to derive altitude temperature profiles. Indeed, the MTP/ER2 instrument has two channels with several overlapping weighting functions (cf. Fig. 6).

 

For angle-scanning multi-channel radiometer systems (used to provide inter-channel calibration) there is no absolute calibration amplification when deriving averaging kernel estimates of air temperature. There is stochastic noise amplification, but this can be made quite small by using wide bandwidths, low-noise amplifiers, or by averaging measurements. The practical limits to using averaging kernels approaching the "ideal" shape are set by other factors. They are set, for example, by the accuracy with which weighting function shapes can be assumed  -  due to slight errors in observing frequency, or uncertain knowledge of the physical constants producing absorption coefficients, Kv, or slight inhomogeneities in the Kv(r) profile (caused by aerosols, water vapor, clouds, etc). 

 

The angle-scanning multi-channel radiometer system concept cannot be used for improving horizontal gradient measurements. Such systems will probably always be subject to the full impact of absolute calibration amplification. 

 

Statistical Retrieval Procedure

 

The "statistical retrieval" (SR) procedure is a favorite method for converting remotely-sensed observables to desired physical properties, called "retrievables." It is an all-purpose tool that has found applications in many fields besides remote sensing. The same factors that render it powerful also render it dangerous on occasion. It must be used carefully, with awareness of limitations and pitfalls. Since each situation can usually be served by many possible retrieval procedures, it is important that careful thought be given to their strengths and weaknesses in relation to the intended use. Sometimes the SR procedure may not offer the best match to the user's needs. This sub-section will briefly sketch how the procedure works, and highlight its main strengths and weaknesses. (The executive reader can read this sub-section "quickly.")

 

It will be useful to think in terms of "reality space" and "observable space." In reality space are the things we want to have values for, such as air temperature at a specific altitude (or specific range). In observable space are the things our instruments measure, such as brightness temperature at specified frequencies and viewing directions. Both "spaces" can have any number of dimensions. It is straightforward to calculate where in observable space a set of measurements should be if we first specify the reality space location. This assumes, of course, that we have complete knowledge of the physics governing thermal emission and intervening absorption and scattering. There are no ambiguities transforming in this direction. For every hypothesized location in reality space our physical model "maps us over" to only one location in observable space, as illustrated by situations A, B and C in Fig. 14 (note that realities B and C map to the same location in observable space).

 



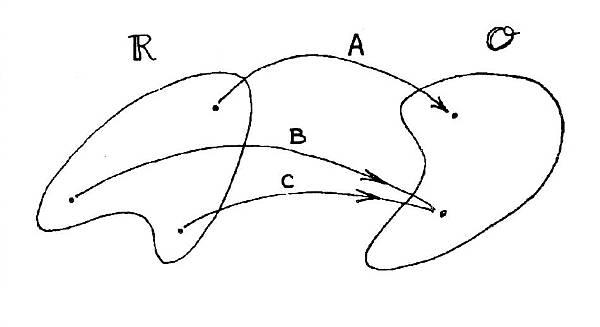
Figure 14. Mapping over from Reality Space to Observable Space.




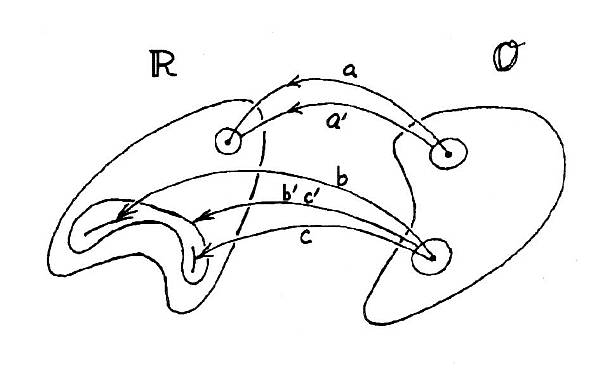
Figure 15. Mapping back from Observable Space to Reality Space.


It is not straightforward "mapping back," going from observable space to reality space. Indeed, there are ambiguities, in which one location in observable space maps over to many points in reality space, as illustrated by situations "b" and "c" in Fig. 15. This situation can occur when observables are integrated quantities, like brightness temperature. When observing uncertainties are taken into account we are dealing with mapping back from areas in observable space to areas in reality space, as shown by a' in Fig. 15. For the situation in which more than one reality produces identical (or nearly identical) observables a small area in observable space can map back to a large area in reality space. This is depicted in Fig. 15 as situation b'c'. 

 

These examples illustrate how care must be taken in transforming observables to an inferred reality. It is necessary to assure that the "best" solution is obtained, and to assure that formal uncertainties take proper account of the mapping ambiguities. Sometimes the "best" solution is one that is known to occur often in reality, even though its corresponding observables are no better than those corresponding to some alternative reality. The SR procedure can be used to do a powerfully good job of this.

 

The SR procedure consists of two parts. First an archive is created, consisting of paired sets of realities and observables. For example, we might begin with 100 radiosondes. For each radiosonde we note the values of the parameters we want to retrieve and we calculate what the observable values should be (using a good physical model and a perfect measuring instrument). This will produce 100 sets of observable locations paired with their corresponding reality locations. (The use of the term "location" is merely a shorthand way of referring to a set of values, corresponding to a "vector" in either observable or reality "space.") In the example just cited, the observables are "simulated" using a believable physical model. 

 

It is also possible to use real measurements in the SR analysis, perhaps taken specifically for creating an SR archive. Using real observables in the SR analysis is a variant which is less commonly used due to the greater cost compared with using computer simulations. It is a superior option that may justify the additional cost since real observables contain idiosyncracies of the measurement system. However, the retrieval coefficients obtained using real observables might not be useable with an upgraded observing system with fewer, or different, idiosyncracies.

 

The second part of the SR process is to calculate "retrieval coefficients" that will enable a transformation to be made from observable space to reality space. The transformation is made using a simple linear series:



 

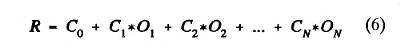
where R is one of the retrievables, Oj are the observables, and Cj are the retrieval coefficients (and there are N observables). Any set of values for Cj will transform from observable space to reality space, but there is one set of values for the coefficients that will do this job with a minimum RMS residual between the archive reality values and the retrieved reality values. The trick is to find that one optimum set of values for Cj so that this minimum variance is achieved. 

 

The set of C values is a vector (of dimension N+1). It is theoretically possible to locate the desired location in "N+1"-dimensional space by a "brute force" method of searching all reasonable combinations for Cj-values and keeping track of the RMS variance performance for each. But there's a better way to locate the best set of values for the C vector. It requires that two covariance matrices be calculated.

 

First, the matching sets of observable and reality vectors must be "conditioned," or expressed as differences from their ensemble averages.




Then the "cross-covariance" and "auto-covariance" matrices are calculated, SRO and SOO.  SRO contains information on all the correlation combinations between the conditioned retrievables and observables (summed over all simulation cases), and SOO consists of all the correlation combinations between the various observables (summed over all simulation cases). The SOO matrix is then inverted, and multiplied with the SRO matrix, producing a matrix that is the desired C matrix of optimum retrieval coefficients. If there are i retrievables (reality parameters) and j observables, then the C matrix is a "j by i" matrix. It is possible to make allowances for a priori measurement uncertainties by creating an "error matrix" and adding it to the SOO matrix before it is inverted.

 

The reader who wants details about any of these matrix manipulations is referred to other more lengthy treatments, such as that of Westwater (1972). The already lengthy description given here is meant to convey a flavor for what "goes into" the derivation of SR coefficients. The astute reader will recognize that virtually any measurable quantity can be used as an observable. For example, the "price of eggs" might have a useful correlation with air temperature at a specific altitude, and the formalism can accommodate the inclusion of this and other more outrageous observables!

 

It is important to be mindful of some strengths and weaknesses of the SR procedure. The SR coefficients provide a minimum variance between the archive retrievables and the retrieved retrievables. If the archive contains many representations of a particular situation, that situation will be "favored" in subsequent uses of the SR coefficients. Equally good solutions will be "unfavored." This may be considered a strength, or a weakness, depending on the nature of the observing situations for which the statistical retrieval coefficients are to be used, and depending on the objectives. It is a strength when future observing situations are similar to the archive giving rise to the SR coefficients and when the proper retrieval of common situations is to be emphasized. It is a weakness when future observing situations will not be similar to the archive, or when the proper retrieval of uncommon situations is to be emphasized. 

 

The SR procedure is only valid for the range of reality situations encompassed by the archive used to generate the coefficients. When novel conditions are encountered, or a new environment is entered, there is no guarantee that the retrieved reality will be reasonable. If this can be anticipated it is sometimes possible to attempt to allow for this by artificially supplementing the archive with situations that endeavor to include the unusual or novel conditions. The "wider" the archive the poorer the performance in the most common reality area. So there are trade-offs in trying to allow for too many unusual situations.

 

Bracewell Retrieval Procedure

 

The radio astronomer Ronald Bracewell employed an iterative procedure for reconstructing brightness temperature distributions on the sky from beam-smoothed measurements of intensity versus sky location. I later adapted these procedures for sharpening 2-dimensional maps of the moon's microwave brightness temperature distribution. The method is extremely simple, and I will describe the procedure for recovering 1-dimensional structure of any source function from observations that are smoothed versions of the source function.

 

Bracewell's method for extracting structure involves the observed distribution of anything versus something else. There is a true source function (the thing we want) and a measured function (the thing we observe). During the Bracewell iterations we hypothesize a source function and calculate an observed function using an adopted smoothing function. For the case of extracting spatial structure the smoothing function would be the antenna pattern and the source function is the true distribution of intensity versus angular location. For the case of extracting air temperature versus range the smoothing function would be the observable weighting function and the source function would be the profile of air temperature versus altitude.


 


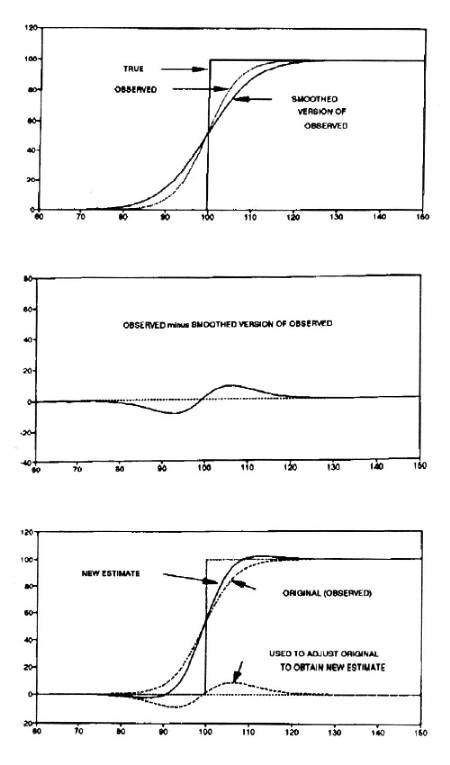
Figure 16. Distribution shapes during the first iteration cycle of a Bracewell procedure for recovering structure.


The first step is to adopt the observed function as a hypothetical true function. This hypothetical true function is smoothed using the known smoothing function, and the resultant smoothed function is compared with the measured function. If agreement is "adequate," the procedure stops and the hypothesized true function is accepted as true (even though no adjustments had been made). No adjustments are needed when there are no "sharp" structures in the true function (causing the observed function to equal the true function). 

 

If the hypothesized function produces a predicted hypothesized observed function that departs significantly from the actually observed function, then an adjustment to the hypothesized function is required. A departure function is defined as the "predicted hypothesized observed" function minus the "hypothesized" function. This departure function is subtracted from the hypothesized function to produce a new hypothesized source function. This completes one iteration cycle. The iterations are performed until the departure function is "acceptable." It is important to "know when to stop" with the iterations. Stopping too soon produces a solution that is too smooth, with unextracted structure "in" the observables. Stopping too late leaves unreal structure in the solution, created by the magnification of observable noise. 

 

In computer simulations of spatial structure recovery, with hypothetical true functions and typical observable smoothing functions and observable noise, I have found that approximately 5 iterations is often close to optimum. When the true function does not contain high spatial frequency components the solution stabilizes (successive hypothesized functions do not change) after fewer iterations. When the true function is "rich" in high spatial frequency structure, however, solutions do not stabilize and noise magnification can degrade solutions past 5 or 6 (depending on the signal to noise ratio, etc). 

 

There are Fourier decomposition ways of understanding what the Bracewell method is accomplishing, which are probably obvious to the astute reader. In fact, the reader may wonder why it is not better to decompose the observed function into its Fourier components and multiply them by the inverse of the amplitude of the corresponding Fourier components of the known smoothing function to obtain a solution function. Indeed, this can be done (after proper "windowing" of the observed function), and quite extensive and sophisticated procedures for sharpening structure have been developed by many workers in many fields. I will not describe them here because the Bracewell procedure is computationally simpler, its implementation is straightforward, and it serves to illustrate the concept.

 

In using the Bracewell method for recovering structure it is necessary to assume something about the observed function beyond the edges of the observed field. In some cases the observed levels have reached zero at the edges and it can be assumed that the observed function remains at this value for all unobserved locations. Other situations do not lend themselves to such easy assumptions. For the situation of measuring air temperature versus altitude it is necessary to assume that the unobserved observable function is a simple extrapolation of trends just inside the observed boundaries. When this assumption cannot be made, or when the unobserved region cannot be represented properly, the Bracewell solution will not be valid near the edges.

 

The Bracewell method is useful when the statistical method cannot be used (because there is no archive of actual past conditions from which to create retrieval coefficients), or when it is "too much effort" to calculate statistical retrieval coefficients. It's main value is speed and simplicity, and a 1-iteration use of the Bracewell method can be used to estimate if there is "recoverable" structure in the observables that may warrant use of a more powerful method.

 

Mutational Retrieval Procedure

 

Biological evolution is a process of "proposing" solutions and having some outside force "select" winners. The winners of each generation are the starting point for "proposing" a suite of slightly altered solutions for the next generation of selection. Mutation is the process of creating slight alterations. As this process evolves there is often an increasing "match" between the "resultant observed properties" and something related to the selective forces. There are some striking resemblances between biological evolution and a novel retrieval process called "mutational retrieval." (The differences are just as interesting, but well outside this tutorial's realm of relevance.)

 

A temperature profile (the concept also applies to temperature versus range) can be described in terms of a small set of parameters, such as temperature at one location, gradient at that location, location of a temperature distortion (such as an altitude temperature profile inversion layer), and properties of this distorted region, etc. The user of the mutational retrieval procedure must give considerable thought to the selection of as few descriptive parameters as possible. It is desirable to create as much "orthogonality" as possible (so that altering one parameter will not have effects similar to those of another parameter). I invite the reader to think of these descriptive parameters as "genes." 

 

An observing instrument doesn't observe the parameters, only the effects of the parameters; or the aggregate effects of all the parameters working together. The sum of the effects of all the parameters is a temperature profile. Only after some thought is it possible for the physical scientist to view the profile as something produced by the sum of effects of individual parameters with specified values. The parameters are a very useful conceptualization even though they are never directly observed. 

 

Not only does the physical scientist never directly observe the parameters that determine a temperature profile, he never observes the temperature profile either. What is observed is merely a set of "observables" which are related to the temperature profile. The observables are related to the temperature profile by the properties of measuring instruments.

 

This is analogous to stating that the forces of selection do not interact directly with an individual's genes, nor with the genotype (the sum of all genes that influence anatomy, physiology, and behavioral predispositions). Rather, the selection forces interact with a "phenotype," the combined expression of the genes influencing anatomy, physiology and behavior. The relation has been described as G + E = P, or Genotype plus Environment produces Phenotype. Phenotypes determine the fate of the underlying genotype elements:  the genes. 

 

The goal of the mutational retrieval procedure is to derive a set of values for parameters describing a temperature profile versus altitude (or temperature versus range, etc) which provide a good match to observed quantities. The process is iterative, somewhat like the Bracewell method. An initial set of parameter values is chosen. Although it is not critical which initialization is chosen, solutions are obtained faster by cleverly converting observed quantities to initial parameter values. The chosen parameter values are used to specify a complete temperature profile (or whichever source function is appropriate). This temperature profile is then used to calculate observed quantities. 

 

The next step is a comparing process. The "predicted observed" quantities are compared with the "actual observed" quantities, and the discrepancies are used to calculate an RMS fit. A "figure of merit" is calculated which can contain a priori information about expected RMS fit, expected magnitude of lapse rates (it can penalize super-adiabatic lapse rates, for example), or anything else which brings in outside "knowledge." The figure of merit value is stored along with the parameter values which produced it. (This is analogous to the selective forces "measuring" the merits of an individual and noting which constituent genes make up the individual's genotype.)

 

Parameter mutations are next generated (analogous to genetic mutations). It is important to perform mutations on the right number of parameters. Experience has shown that at least two mutations per "generation" is better than just one (some locations in parameter value space cannot be reached by following figure of merit gradients unless two or more parameters are allowed to vary). Experience has also shown that mutations performed on all parameters is inefficient (payoffs can't be accurately ascribed when too many parameters are varying at the same time). For altitude temperature profiling, where approximately 8 parameters are involved, I have found that 2 mutations are close to optimum. Mutation amounts must be pre-specified (other dynamics are possible). As a result of this mutation cycle, an "offspring" is produced! 

 



Figure 17. Flow of operations in performing "mutational retrieval." Begin in lower-left corner; end when "Figure Merit" is acceptable.

The new ("offspring") parameter set is run through the previously described cycle of "temperature profile generation" and "figure of merit assessment." If the offspring's figure of merit is better than the "parent's," the offspring parameter set becomes the new "parent" for the next iteration. If, on the other hand, the parent's figure of merit is better, the parent remains a parent for the next iteration.

 

After each iteration, if the figure of merit exceeds a threshold (set beforehand) the evolutionary search ends and the winner is declared! This process can produce quite good agreement in "observable space." Since sharp structures composed of straight-line segments are indeed a property of real atmospheres, and since sharp structures composed of straight-line segments are easily produced with parameters describing temperature profiles, some remarkable structure recoveries are achievable using the mutational retrieval procedure.

 

Computational speed is one potential limitation for this method, however. This is intuitively understandable considering that an 8-parameter temperature profile representation requires that an 8-dimensional parameter space be searched for an "optimum" solution. In my experience (with a 20 MHz PC clone with an 80387 microprocessor) it is possible to find a solution in 10 to 20 seconds (involving 50 to 100 "tries"). A 80486 computer should find solutions in less than 5 seconds.

 

The down-side of the mutational retrieval procedure is that an efficient and accurate use of it requires that many subtleties be overcome. It is not a solution for everyone as it must be implemented by someone experienced in the "art."

 

PREVIOUS APPLICATIONS DESCRIPTIVE REVIEW

 

Microwave radiometric studies of the atmosphere can be assigned to the following three application categories: 1) ground-based remote sensing of atmospheric properties, 2) satellite-based remote sensing of atmospheric properties, and 3) aircraft-based remote sensing of atmospheric properties. The above sequence approximates the order in which these sub-discipline began, and it is ironic that aircraft applications followed satellite usage. Ground-based systems have been constructed since the late 1960s, satellite payloads for earth studies began in the mid-1970s, and the first aircraft instrument was flown in 1978 (Gary, 1981). The following sub-sections describe atmospheric temperature profiling highlights from the first and third categories. 

 

Two groups have dominated ground-based temperature profiling work: NOAA's Wave Propagation Laboratory (headed by Ed Westwater), and NASA's JPL (headed by Bruce Gary). The early work in this field was done by the NOAA/WPL group (from the late 1960's to the early 1970s). During the late 1970s the two groups collaborated closely, since WPL was weak in hardware (where JPL was strong) and JPL was weak in retrieval theory (where WPL was strong). Since the early 1980s, as the two groups strengthened their respective weak areas, there has been a lessened need for collaboration.

 

I will review radiometer systems built by the JPL group because I am familiar with them and they adequately represent the flavor of capability improvements during this period. It might be of interest to note that there are some minor "philosophical differences of approach" between the two groups which can be accounted for by the slight differences in goals and previous capabilities within the WPL and JPL environments. The WPL group emphasizes large, stable systems that are meant to take data in one location for years at a time, while the JPL group emphasizes small, portable systems that can be deployed easily at remote locations and supported by field personnel. It is not surprising that JPL's approach emphasizes smallness, considering JPL's history of building satellite instruments. 

 

Since airborne temperature profiling has been conducted by only the JPL group, all examples in this category will be from work done by us (since 1977).

 

Ground-Based Temperature Profiler MIST

 

JPL built a ground-based temperature profiler in 1975 to study the feasibility of placing microwave temperature profilers on deep ocean, moored data buoys for the purpose of supplementing the National Weather Service's radiosonde network to improve weather forecasts. Measurements were made at Point Mugu, CA in 1976 in collaboration with NOAA/WPL, showing that air temperature and vapor profiles could be inferred using a 3-frequency, angle-scanning radiometer. MIST operated at 22.3, 31.4, 54.0, 55.3, and 57.5 GHz. 

 

In 1977 the MIST system was deployed aboard the weather ship Quadra, which was stationed at a fixed location in the middle of the Gulf of Alaska. NOAA/WPL analyzed MIST data, and showed that there was excellent agreement between predicted and achieved performance for temperature profiles, from surface to over 30,000 feet, and vapor profiles from surface to 15,000 feet.

 

Measurements were made again in 1978 with the same instrument at the Boulder Atmospheric Observatory 1000-foot atmospheric research tower, during the PHOENIX project, in collaboration with NOAA/WPL. Good air temperature profile performance was demonstrated. 

 

Ground-Based Temperature Profiler MARS

 

JPL built a Microwave Atmospheric Remote Sensor system, MARS, for participation in EPA's 1980 PEPE (Persistent Elevated Pollution Episodes) experiment. After 5 days of data in Croton, OH, MARS was struck by lightning, which terminated the MARS participation in PEPE.

 

MARS was repaired, and in March of 1983 it was deployed at Buffalo, NY to demonstrate the feasibility of monitoring overhead aviation icing hazard (Gary, 1983). An 8 to 14 micron IR radiometer was added to MARS to allow cloud base determination. Real-time altitude profiles of icing hazard were inferred, and a dial-up capability was achieved. An integrated hazard was correlated with pilot reports of icing encounters, and scoring boxes were constructed that can be described as very encouraging. 

 

MARS was operated at Denver's Stapleton Airport for a 12-month period in 1985/86 with the intent of determining how well a mobile temperature profiling system would operate in an unattended mode for retrieving air temperature profiles. As in previous evaluations, radiosondes served as a reference standard, and good RMS agreements were achieved: 1.0 K for altitudes below 2000 feet, <2.0 K from 2000 to 10,000 feet, and <3.0 K from 10,000 to 20,000 feet. This performance is essentially the same as pre-experiment predictions. 

 

Ground-Based Temperature Profiler BUOY

 

JPL built a very compact unit combining a temperature profiler with a water vapor and liquid (cloud) water radiometer intended for installation on a NOAA data buoy. It was to telemeter data via geosynchronous satellite to a Weather Service forecast center. NOAA administration changes canceled plans to follow through with the implementation of the radiometer on a buoy, and it was decided to test the system at Denver's Stapleton Airport for a 1 year evaluation period prior to turning it over to NOAA/WPL. This 1 year test was conducted in 1985/86, and JPL's data analysis showed that the desired performance had been achieved. (It was then turned over to NOAA/WPL, where it was disassembled for parts).

 

Ground-Based Temperature Profiler PMTP

 

JPL constructed a compact microwave temperature profiler, called Passive Microwave Temperature Profiler, or PMTP, which was delivered to the U. S. Army in 1988. It uses 4 frequencies from 51 to 58 GHz, and scans through 5 elevation angles from 9 degrees to zenith. The 51 GHz channel serves to monitor cloud liquid content (a novel idea which no other temperature profiler incorporates), while the other three channels measure the temperature profile. This radiometer system is probably the best portable microwave temperature profiler in existence.

 

Ground-Based Temperature Profiler MTP/DOE

 

The MTP instrument that is usually installed in the ER-2 aircraft was modified temporarily for ground-based use for a 1991 March deployment in Platteville, CO. Many other remote sensors were deployed at the same time and location on behalf of the Department of Energy's Atmospheric Radiation Measurements (ARM) part of the  Winter Icing Storms Program, WISP. The MTP was tilted upward 34 degrees to optimize the elevation sampling for retrieving temperature profiles. The low frequency MTP channel was changed to a lower value, so that it would be less redundant with the other channel, but this channel failed and only 1-channel MTP/DOE data was obtained. Data analysis is now in progress. 

 

Airborne Microwave System MTP/CV990

 

The first airborne microwave temperature profiler instrument, MTP/CV990, was built by JPL in 1978 and installed in NASA's CV-990 "Galileo II" (Gary, 1981). This instrument participated in the 1979 NASA-sponsored Clear Air Turbulence Flight Test Program (Weaver, et al, 19??). The CV-990 compliment of instruments included four CAT-related sensors: 1) a 10.6 micron lidar built by NASA's Marshall Space Flight Center, 2) a 30 micron IR radiometer (Kuhn, 1980), 3) JPL's MTP/CV990, and 4) a JPL 183 GHz water vapor burden radiometer. 

 

MTP/CV990 is a modified version of the engineering model of the Scanning Microwave Spectrometer (SCAMS), the flight model of which flew in the NIMBUS-6 weather satellite. MTP/CV990 operated at 55.3 GHz, and scanned from 16 degrees below to 20 degrees above the horizon every 17 seconds. A microwave "transparent" window had to be 1-inch thick to support cabin to outside pressure differences, and even with anti-reflection grooves on both sides the window losses were 6% (3% due to absorption and 3% due to reflections). 

 

This first flight series with an MTP instrument showed how useful MTP could be in locating the altitude of the tropopause, where most commercial aircraft CAT is encountered. These flights also provided evidence that inversion layers were also sites for CAT production. MTP/CV990 data was used to produce a first-ever time-lapse movie of airborne ATP shape variations.

 

Airborne Microwave System MTP/C141

 

JPL's next MTP instrument was built for NASA's C-141 Kuiper Airborne Observatory (Gary, 1984). MTP/C141 (see Fig. 18) was a 1-channel radiometer, operating at 56.0 GHz, and installed in the right wheel well. The entire front end assembly (horn, mixer, IF amplifier, detector) moved to produce elevation angle scans every 30 seconds. Real-time displays of air temperature versus altitude were presented on a rack-mounted monitor. 

 

Approximately 450 flight hours of measurements were obtained during the years 1981 to 1985. Approximately 15% of the flight data was near the tropopause, and it was determined that there was a greatly enhanced probability of encountering CAT during flight near the tropopause (19% of 10-minute segments contained moderate or greater CAT) compared with flight in the troposphere (2.7% CAT) or stratosphere (1.7% CAT). Furthermore, two tropopause "altitude temperature profile" shapes had different CAT probabilities:  the simple 2-segment shape had a 13% probability of CAT whereas the 3-segment, inversion layer shape had a 24% probability of CAT. 




Figure 18. This MTP instrument was flown in NASA's C-141 Kuiper Airborne Observatory during 4 years in the 1980s. It was used to study the association of CAT encounters with tropopause temperature profile shape types.


JPL's third MTP instrument is called MTP/ER2. It was installed in NASA's ER-2 aircraft in 1985. The section "Altitude Temperature Profiles" (pp 7-9) describe some aspects of MTP/ER2. It was used in the 1987 Stratospheric/Tropospheric Exchange Project, STEP, the 1987 Airborne Antarctic Ozone Experiment, AAOE, and the 1989 Airborne Arctic Stratospheric Expedition, AASE. At the present time this is the only airborne atmospheric temperature profiler in use (since the two predecessor MTP instruments have been "retired"). An upgraded version of it will participate in the 1991/92 "Airborne Arctic Stratospheric Expedition II," AASE II, to be based in Bangor, Maine.

 

The entire instrument weighs 58 pounds, much of which consists of 1984-vintage power supplies (which are now being replaced with lighter ones).  MTP consists of two units: a sensor unit, weighing 10 pounds, and a data unit, which is in the process of being lightened to an estimated 35 pounds (including 15 pounds of power supplies). The dimensions are 13 x 7.5 x 5 inches for the sensor unit, and 18 x 14 x 9.5 inches for the data unit (the new data unit design is 17.5 x 8.75 x 7 inches).


MTP/ER2 SU inside


Figure 19. This MTP has flown in NASA's ER-2 aircraft since 1985. It is more compact than the earlier C-141 MTP, because it employs a smaller horn and a shaped reflector which scans.


The sensor unit consists of a scanning shaped reflector and horn antenna, a microwave mixer operated in a total power mode, an IF amplifier and detector, and a voltage-to-frequency converter. Two local oscillators are turned on in turn, operating at 57.3 and 58.8 GHz. The IF bandpass has been 190 to 390 MHz during previous deployments, but it now is 265 to 375 MHz. A noise diode is injected between the horn and an isolator, and provides a calibration signal of approximately 50 K. The double-sideband noise figure is approximately 4 db, which produces a stochastic noise level of 0.12 K for each 255 millisecond reading. Baseline "wander" adds a component of approximately 0.2 K to the stochastic noise, producing a net RMS uncertainty of 0.3 K. The accuracy of these readings is estimated to be 0.5 K.

 

The horn antenna/shaped reflector assembly provide a beamwidth of 7.5 degrees (FWHM). The beam is scanned through the following sequence of 10 elevation angles every 14 seconds: -50, -35, -22, -11, 0, +10, +20, +31, +44, and +60. At each elevation angle 255-millisecond readings of the total power radiometer output are made at both frequencies. Each 14-second cycle includes readings taken while viewing an ambient calibration target. An inclinometer is read prior to each scan to provide an elevation angle offset which corrects for aircraft pitch changes. A vertical accelerometer is located in the data unit, and values from filtered maximum and minimum excursion circuits are recorded. Aircraft synchro signals convey pitch, roll, and pressure altitude information to the microprocessor in the data unit. A microprocessor records the radiometer readings, instrument temperatures, aircraft synchro signals, and clock readings. The recording medium has been a cassette tape unit, with a 0.5 Mbyte capacity (good for an 8-hour flight). We are currently installing a 40 Mbyte hard disk removable recording unit. Other engineering details can be found in Denning et al (1989). The first published description of MTP results can be found in  Gary (1989). 

 

MTP data have been presented in several forms, and each is useful for different things. The most straight-forward form is an "altitude temperature profile," or ATP. Figure 10 is a sample of an ATP. Successive ATP traces are offset by specified amounts along the x-axis, and a glance of such a presentation shows whether interesting vertical temperature structures are present and if they are changing. Passage through the tropopause is easily noted from an ATP presentation. The presence of inversion layers are also easily noted, and estimates can be made of the altitude of the inversion layer's top or bottom. 

 

Another form for presenting MTP data is a simple plot of lapse rate, LR, versus time. Figure 20 plots LR versus time for a flight that went from Chile to the Antarctic Peninsula and back. Most of this data is in the stratosphere, where LR is generally isothermal (LR=0).  In the troposphere LR values are typically in the range -7 to -10 K/km, with occasional shallow inversion layers (LR>0) and occasional surface-based super-adiabatic layers (LR more negative than -10 K/km) that extend to possibly 100 meters above the surface. The beginning part of the LR plot in the figure is during flight in the troposphere, where LR » -8 K/km. During passage through the tropopause, the boundary separating the troposphere from the stratosphere, a brief LR peak occurs, where LR » +8 K/km. At about 61,000 UT seconds LR dips to » -8 K/km. This is a real "almost adiabatic" feature. The trace in Fig. 18 may appear "noisy" but all excursions shown are greater than LR measurement noise and they are therefore "real."


LR(t)


Figure 20. Sample MTP plot of lapse rate versus time for a flight over Antarctica. 

 

LR is one ingredient for inferring "potential vorticity," PV.  PV is the product of the vertical gradient of potential temperature (easily derived from LR) and the horizontal gradient of wind speed.  PV is a useful property of air parcels with horizontal extents ranging from kilometers to more than 100 km.  It is useful because it is "conserved" on timescales shorter than a few weeks.  Thus, if a stream of air penetrates a larger air mass, important constraints can be placed on the origin of the "streamer" by measuring its PV.  PV continues to be an important atmospheric parameter used in airborne studies of ozone depletion. 

 

Another form for presenting MTP data is something that can be called an Isentrope Altitude Cross-section, or IAC.  To understand an IAC it is necessary to first understand the atmospheric properties "potential temperature" and "isentrope."  Potential temperature is a conserved property of air parcels (meters to kilometers in size); it is the temperature an air parcel would have if it were "brought to" the 1000 millibar altitude adiabatically (without allowing energy to enter or leave the parcel).  The potential temperature of air can be calculated by the formula:

 

                θ = T * (1000/P)0.27

 

An isentrope is a surface of the atmosphere having the same "potential temperature."   An IAC is obtained by calculating the altitudes of specific isentrope surfaces versus flight time, or the corresponding ground-track location.  Since an aircraft's ground track is not always a straight line actual cross-sections are often referred to as "curtain cross-sections."  An IAC, therefore, can be more accurately described as an "isentrope altitude curtain cross-section."


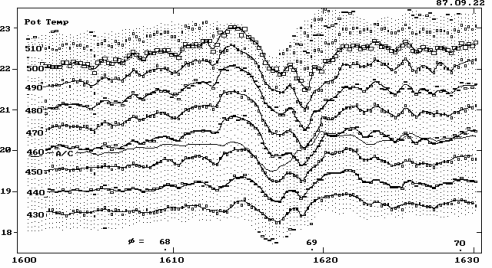
IAC of mountain wave


Figure 21.  Sample IAC, Isentrope Altitude Cross-section, obtained from the MTP/ER2 instrument, showing a "mountain wave."

 
Figure 21 is a sample IAC.  It was the first IAC produced, during the 1987 AASE mission to Chile, and coincidentally it exhibits the best portrait of a mountain wave that has been obtained to date from the MTP instrument. The wavy pattern shows isentrope displacements as large as 600 meters in the 22 km altitude region. A thin line denotes the ER-2 aircraft's altitude flight through this atmosphere, and downdrafts and updrafts (as large as 7 m/s) were encountered that caused the ER-2 to undergo altitude excursions of almost 1 km. The isentrope displacements are caused by a mountain below the aircraft. 

 

Since potential temperature is "conservative," isentropes can be used to locate streamlines for air motion (provided the IAC is in a plane approximately parallel to wind vector). The isentropes in Fig. 21 imply parcel cooling (during the upward displacements) of as much as 6 K, and warming (during the downward displacements) of the same amount. If the frost point depression is less than the amount of the cooling, then a cirrus lenticular cloud will form at the top of the upward isentrope displacement. This phenomenon was documented during another flight over the Antarctic Peninsula during the same mission. Such clouds in the polar regions are called polar stratospheric clouds, or PSCs. PSCs are now known to be a key factor in producing the ozone hole over Antarctica. No other airborne instrument is able to produce IACs, and those that can be produced from satellites or radiosonde networks have incomparably poorer vertical and horizontal resolution.

 

Data acquired by the MTP/ER2 instrument was used to derive a method for determining vertical wind shear, VWS.  VWS can be combined with lapse rate to infer the value for the Richardson Number, which is a key atmospheric property for predicting CAT. The procedure for doing this is the subject of a NASA patent application.

 

Airborne Microwave System MTP/DC8

 

Currently under construction, the JPL-built MTP/DC8 will be installed in NASA's DC-8 research aircraft in October, 1991. Figure 22 is a sketch of the instrument. It will be a "many frequency" radiometer, since it will be able to tune continuously between 55 GHz and 59 GHz. In this band there are, in effect, only 7 useable frequencies since it is only useful to set the local oscillator to frequencies in the valleys or peaks of the oxygen spectrum. MTP/DC8 will scan from nadir to zenith in approximately 15 seconds.


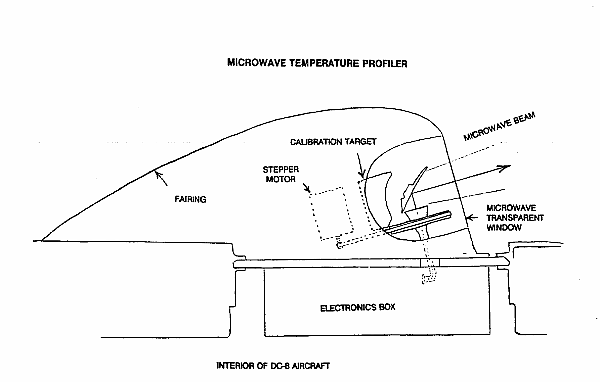
SKetch of MTP/DC8


Figure 22.  Sketch of MTP/DC8, looking down. MTP is installed in a window frame on the left side of the DC-8 aircraft.
 
Simulations show that this instrument will be able to produce useful "altitude temperature profiles" extending from 4 km to about 30 km. Figure 23 shows predicted performance for altitudes above flight level (assumed to be 12 km).

 

The MTP/DC8 data will be used during the AASE II mission in 1991/92 to: 1) locate altitudes where it is cold enough for PSCs to form, 2) assist in measuring potential vorticity (to locate the polar vortex boundary), and 3) study characteristics of the mesoscale up and down displacements that may influence PSC particle size distributions.


Predicted MTP/DC8 RMS(z) performance


Figure 23. Predicted RMS uncertainty of retrieved air temperature using the MTP/DC8 instrument. 

Airborne Microwave System MTP/RKW

 

The newest MTP instrument is in design and is scheduled for delivery to Rockwell International. Functionally, it will be very similar to the MTP/DC8 instrument; but in physical layout it will be more like the existing MTP/ER2. It will be capable of continuous frequency sampling in the interval 55 to 59 GHz, using a VCO (voltage control oscillator) under computer control.

 

During  en route flight it will scan a 7 degree beam from nadir to zenith in 15 seconds. At each viewing direction it will sample a set of 5 to 7 frequencies, and produce ATPs (altitude temperature profiles) that span 6 to 13 km (for an assumed flight level of 11 km). (It is not necessary to determine the ATP above this region since step climb possibilities are limited to 1 or 2 km above en route flight level; and knowledge of profiles beyond several km below flight level are not useful). The intended use of MTP/RKW during en route flight is to provide warnings of CAT, as well as altitude guidance away from the CAT.

 

In the terminal area the MTP/RKW will scan a smaller range of elevation angles but sample the full range of frequencies in an observing sequence designed to optimize the measurement of 1) lapse rate near flight level, and 2) horizontal air temperature gradients ahead of the aircraft. The intended use of this data is to assist in providing warnings for "low altitude wind shear," LAWS.


Airborne Microwave System MTP/MMIC

 

It is anticipated that future versions of the MTP will incorporate MMIC (microwave monolithic integrated circuit) technology. This will be especially important for the design of light weight and low cost MTPs for use in commercial aircraft (where cost and reliability are important) and unmanned aerial vehicles, UAVs (which have modest payloads). Without using MMIC techniques an MTP could be built that would weigh approximately 10 pounds. We anticipate that by using MMICs it will be possible to build an MTP weighing 1 or 2 pounds (plus the fairing and computer). Such a system would employ a MMIC radiometer and a MMIC electrically-steered antenna. The cost for MTP/MMIC systems would be much less than non-MMIC MTPs, perhaps $5000 instead of $200,000. 

 

REFERENCES

 

Denning, R., S. Guidero, G. Parks, B. Gary, "Instrument Description of the Airborne Microwave Temperature Profiler," J. Geophys. Res., 94, p. 16757-16765, November 30, 1989. 

 

Gary, B. L., "Microwave Monitoring of Aviation Icing Clouds," Final Report, AFGL-TR-83-0271, 1983 November 11.

 

Gary, B. L., "Microwave Monitoring of Overhead Temperature Profiles," Final Report, JPL Report D-4031, 1987 April 13.

 

Gary, B. L, "An Airborne Remote Sensor for the Avoidance of Clear Air Turbulence," AIAA 19th Aerospace Sciences Meeting, AIAA-81-0297, January 12-15, 1981.

 

Gary, B. L., "Observational Results Using the Microwave Temperature Profiler During the Airborne Antarctic Ozone Experiment," J. Geophys. Res., 94, p. 11223-11231, August 30, 1989. 

 

Weaver, E. A., L. J. Ehernberger, B. L. Gary, R. L. Kurkowski, P. M. Kuhn, L. P. Stearns, "The 1979 Clear Air Turbulence Flight Test Program," NASA Special Publication ???, 19??.

 

Westwater, E. R., "Ground-Based Determination of Low-Altitude Temperature Profiles by Microwaves," Monthly Weather Review, 100, 0. 15-28, 1972.