The following graphs provide details of my solution for a photometric sequence of the star field associated with exoplanet HD 74156 (E0842) made from observations on 2004.12.10 UT. I used a Celestron CGE-1400 (14-inch) configured for prime focus observing using a Starizona transition lens and a SBIG CFW-8 and ST-8XE CCD.

The process begins by measuring "intensity" for all images of the two Landolt fields, LA0452 and LA0853. Coefficients in an equation for magnitude are adjusted until a minimum RMS difference is achieved. The equation has the form:

    EqnMag = C1 + 2.5 * LOG (g / I ) + C2 * m + C3 * (B-V - 0.64) + C4 * m * (B-V - 0.64),

    where,
       g = gate time (exposure time [seconds]),
       I = measured intensity [counts],
       m = air mass (taken from TheSky 6.0),
       B-V = B - V magnitude difference, based on Landolt list

    and constants C1, C2, C3 and C4 have the following meaning:
         C1 = related to telescope aperture and optical throughput,
         C2  = negative of extinction [magnitude/air mass],
         C3 = dependence of telescope system's reponse to star color,
         C4 = star extinction rate dependence on star color.

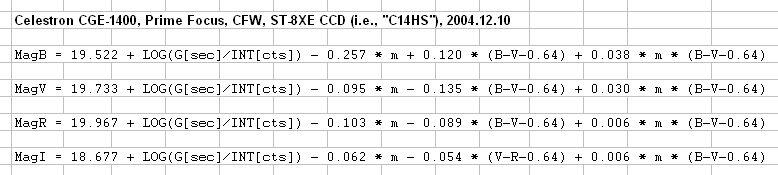
A coefficient solution is obtained for B and V measurements of intensity, using an iterative method described at http://brucegary.net/AllSky/  This solution takes into account the dependence of the B coefficients on V magnitude, and the dependence of V coefficients on B magnitude. For the Lanodlt stars all true magnitudes are known (assumed to be true) so there's no iteration for B and V solutions required at this stage of the analysis. The solution for the four coefficients for this observing night are shown in the next figure.

Figure 1. Equation magnitude solutions for 2004.12.10 UT obsrvations, based on Landolt stars.

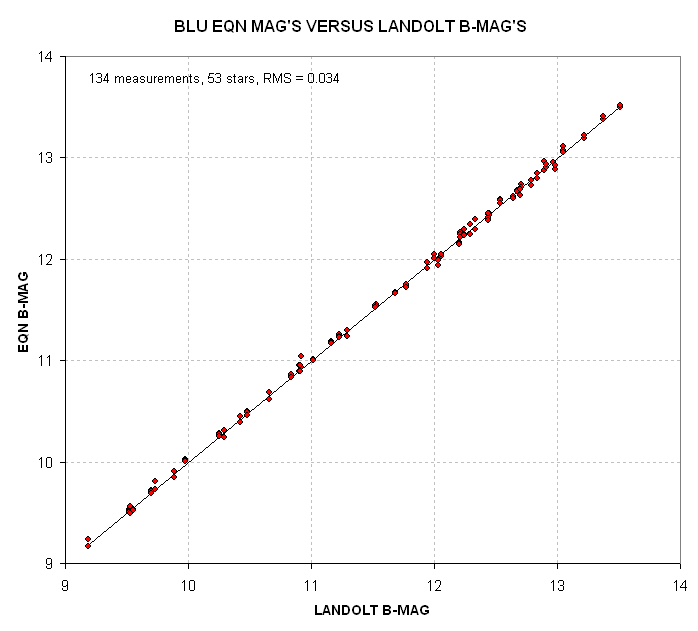
Figure 2. Final Equation B-magnitudes of Landolt stars versus true Landolt B-magnitudes, using the coefficient solution in Fig. 1.

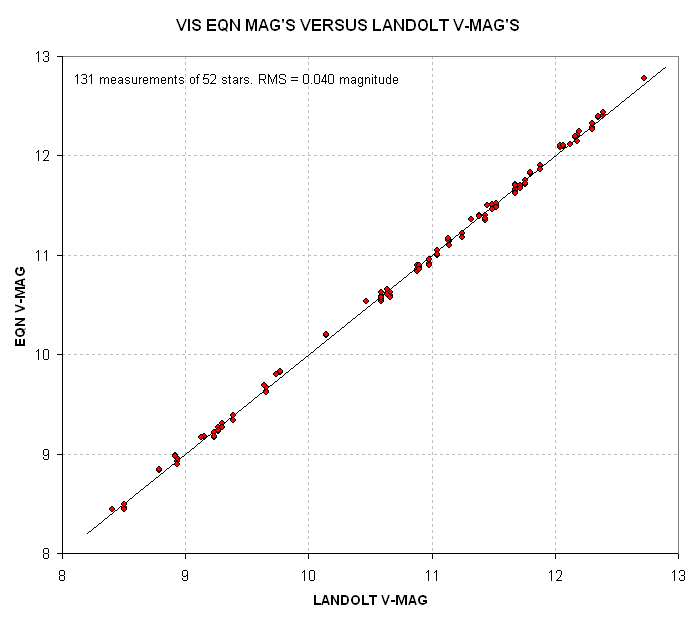
Figure 3. Final Equation V-magnitudes of Landolt stars versus true Landolt V-magnitudes, using the coefficient solution in Fig. 1.

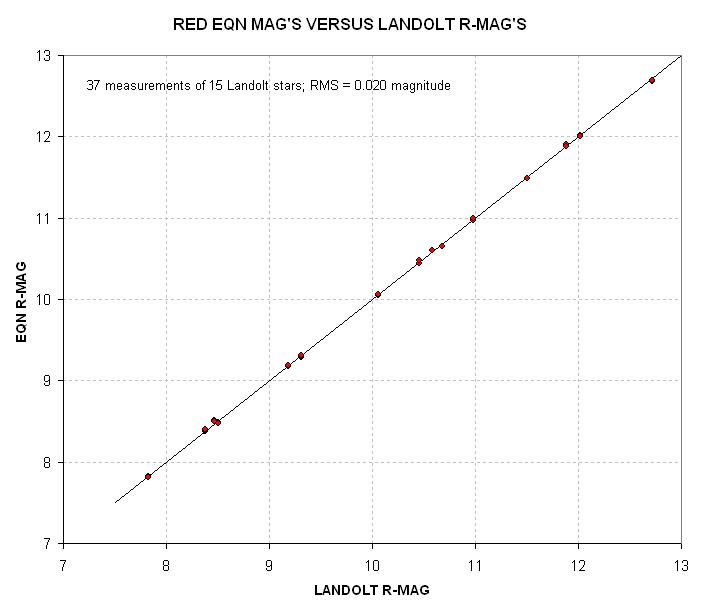
Figure 4. Final Equation R-magnitudes of Landolt stars versus true Landolt R-magnitudes, using the coefficient solution in Fig. 1.

The following graphs show a comparison of my equation magnitudes with Arne Henden's all-sky magnitudes for some stars near the exoplanet HD 74156.

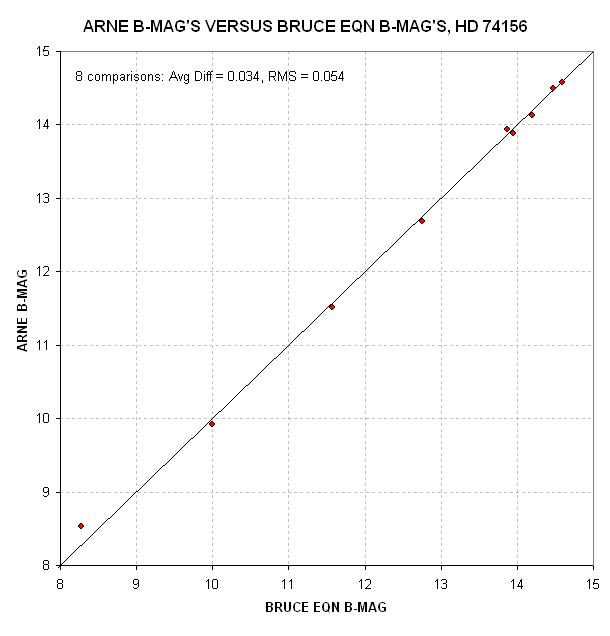
Figure 5. Arne's B-magnitudes versus mine for the 9 stars where our two FOVs overlap. The brightest star (HD 74156) was saturated for Arne and was no used in computing the "average difference" or RMS. .

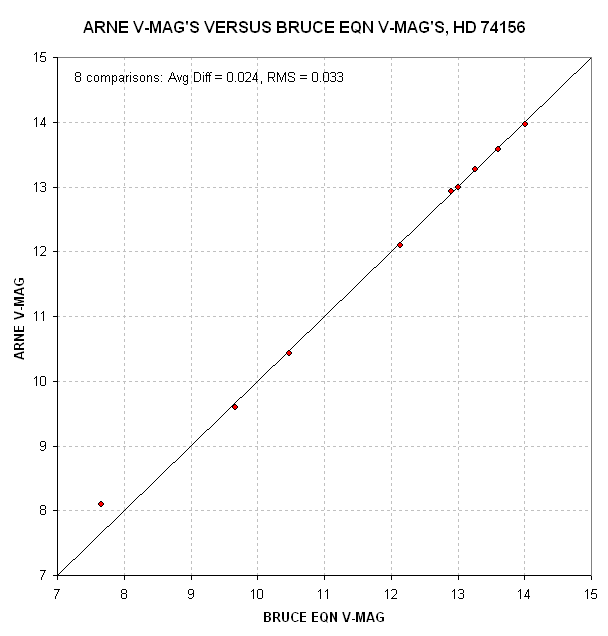
Figure 6. Arne's V-magnitudes versus mine for the 9 stars where our two FOVs overlap. The brightest star (HD 74156) was saturated for Arne and was no used in computing the "average difference" or RMS.

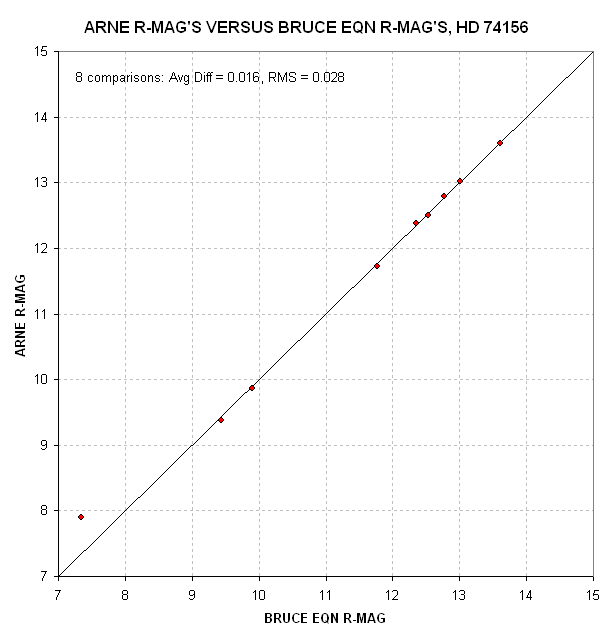
Figure 7. Arne's R-magnitudes versus mine for the 9 stars where our two FOVs overlap. The brightest star (HD 74156) was saturated for Arne and was no used in computing the "average difference" or RMS.

My BVR magnitudes compare well with Arne's, if 0.03 magnitude offsets are conisdered acceptable. Here's a summary of how our two independent magnitude solutions compare for the HD 74156 star field.

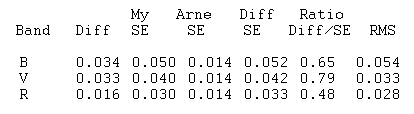
 Figure 8. Summary of differences between Arne Henden and my all-sky solutions for stars near HD 74156.

This site opened:  December 16, 2004.  Last Update:  December 16, 2004