Introduction

Bright stars require that either exposure time be reduced or defocusing be employed. Otherwise the final light curve (LC) will suffer from low duty cycle and therefore loss of precision per unit of pbserving time. This web page describes an observing session of a 9th magnitude star that employed various amounts of defocusing in an attempt to determine if there was a best focus setting. 

Glossary

    dFOC = de-focus value; defined as the difference between PAR75 for a defocused image and a sharply focused image
    DutyCycle = fraction of observing time spent exposing
    FWHM = full-width at half-maximum (applicable for sharply-focused, unsaturated star image; expressed as either "arc or pixels)
    IR1 = information rate, defined in a way that allows for the easy calculation of precision [mmag] for a minute of observing time.
    LC = light curve
    OOT = out-of-transit
    PAR = photometry aperture radius (radius of inner circle; usually expressed in units of pixels)
    PAR50 = photometry aperture radius that encloses 50% of the star's total flux
    PAR75 = photometry aperture radius that encloses 75% of the star's total flux
    PAR98 = defined as radius of circle that contains 98% of defocused star's total flux
    PSF = point-spread-function (regardless of focsus setting)
    px = pixel(s)
    RMS1 = 1-minute equivalent RMS of individual LC magnitudes (preferably, using the neighbor differences method)
                The 1-min equivalence is calculated using RMS1 = RMSi * ( g [sec] / 1 minute)^½) where RMSi is RMS of individual images with exposure time g

Hardware

My telescope is a 11-inch aperture Celestron (CPC1100) mounted on an equatorial wedge. I use a focal reducer and SBIG AO-7 image stabilizer in front of a SBIG ST-8XE CCD camera. The AO-7 employs a tip/tilt mirror that can be operated at several Hz, and when mirror motion exceeds a user-specified limit a correcting nudge signal is sent to the telescope drive motors. The polar axis has been aligned to the north celestial pole with an accuracy of ~2 'arc. This assures that when the AO-7 keeps an autoguided star fixed to a pixel location on the autoguider chip the star field does not rotate about that star and simultaneously move the star field across the main CCD chip. This arrangement assures that the star field is fixed with respect to the CCD pixel field to within a few pixels during the course of a many hour observing session. The image scale is 1.21 "arc/pixel, and the FOV is 31 x 21 'arc. I use a wireless focuser (Craycroft type) for adjusting the position of the optical back-end (the mirror is not moved). MaxIm DL 5.03 is used to control the telescope, wireless focuser, AO-7 and CCD camera.

Each observer's hardware is different, and atmospheric seeing is different each night, so the following is presented with the purpose of illustrating concepts that can be used to guide observers in choosing optimum observing and image analysis strategies.

Review of Usual Strategy for Sharply-Focused Exoplanet Transit Light Curves

Normally, transiting exoplanet light curves are produced using sharply-focused images and a photometry aperture radius (PAR) of about 3 x FWHM. Slightly smaller and larger PAR values can sometimes produce small improvements (e.g., PAR/FWHM within range 2 to 6). When a star is close to the target star it may not be possbile to employ this standard PAR setting. Therefore it is useful to know what penalties are incurred when very small values for the PAR/FWHM ratio are employed.

Here's the star field used for this observating session (2009.01.31):

Figure 1. Star field surrounding target star (red square) and 8 reference stars. FOV = 31 x 21 'arc, north up, east left. FWHM ~ 3.0 "arc. (2009.01.31, median of seven 15-sec images)

Here's a sample light curve (LC):

 
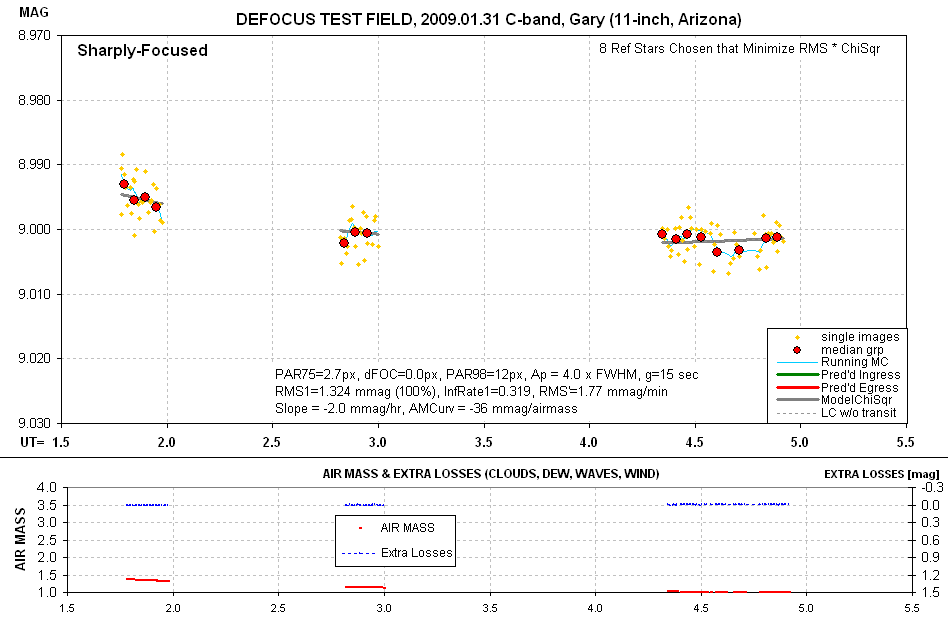
Figure 2. Light curve for sharply-focused images using ApertureRadius/FWHM = 4.0. RMS1 = 1.324 mmag. Other parameters are described in text.

The following figure is a plot of LC precision versus photometry ApertureRadius/FWHM (i.e., PAR/FWHM):

   
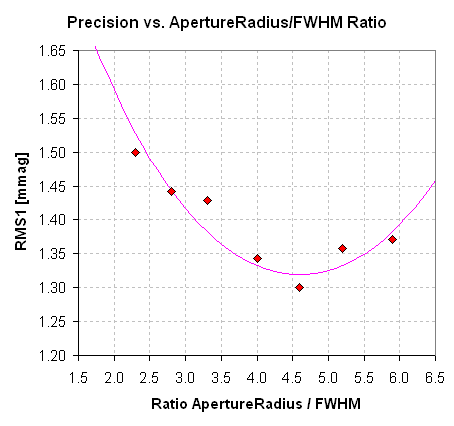
Figure 3. Precision versus ratio ApertureRadius/FWHM for 2 hours of sharply focused observations (102 images).

Fig. 3 shows that for this set of sharply-focused images the "penalty" for departing from the optimum PAR/FWHM = 4.5 is small. Using PAR/FWHM = 2.3, for example, has a precision penalty of ~14%. This corresponds to a 30% observng time penalty (since SNR is proportional to SQRT(ObservingTime)).

Defining Information Rate

Information rate should be defined such that doubling an observing session's length doubles the information acquired (assuming no changes in seeing, etc). When telescopes are compared using the information rate concept it can be surprising to learn that doubling aperture will increase information rate 16-fold. The way to understand this is to ask how much  longer the smaller telescope needs to observe to achieve the same SNR for a given object. The telescope with half the aperture (diameter) has 1/4 the flux of photons incident on the CCD compared to the larger telescope. The ratio of SNRs is therefore 1/4 (assuming all other parameters are the same). To overcome this SNR disadvantage the smaller telescope will have to observe 16 times longer. Hence, the ratio of information rates is a whopping 1:16! This example illustrates the basic concept of information rate.

For a given telescope system it makes sense for the observer to exploit all possible ways to maximize information rate. I want to define information rate for use with exopanet LCs in a way that relates to the "gold standard" of achieving a precision of 1 mmag per minute of observing time! Let's call this version of information rate IR1, and when IR1 = 1 "minutes per mmag" a precision of 1 mmag is achieved every minute of observing time. Amateurs aspire to achieve IR1 = 1, and as far as I know never have, while professionals aspire to never fall below IR1 = 1. An IR1 of 1.0 is what separates amateurs from the professionals, due in large measure to differences in hardware, observing site and software - but also due to differences in knowledge about image processing and data processing. One of the purposes for my tutorials is to "bridge this gap" and raise amateurs as much as possible to the proficiency level of professionals.

Let's derive an equation for IR1 in small steps. First, consider that 4 images should contain 4 times as much information as one image, yet the RMS of the average of 4 images is reduced to only 1/2 the RMS of one image. Thus, information rate is proportional to 1 / RMS². This is the first term in a series of multiplicative terms.

Second, what's the effect of duty cycle on IR1? For reference consider that duty cycle is ~ 1 (negligible download time, and no "settle time" for autoguider reacquisition) and that 1-minute exposures occur every minute. If individual 1-minute images exhibit a precision of 1 mmag, then IR1 = 1 [minutes per mmag]. This is how we're defining the scale for IR1. If, however, duty cycle = 1/2, meaning that two minutes are required to get one image, information rate is reduced to half the original value. Thus, IR1 is proportional to duty cycle.

The product of the first two terms for information rate is then DutyCycle / RMS1², where RMS1 is the precision for 1-minute exposure images.

Third, consider the case in which 2-minute exposures exhibit 1 mmag precision per image. If the exposure time was reduced we know that RMS would increase. If the exposure time was reduced from 2 minutes to 1 minute the simplest calculation is that each image would exhibit an RMS precision that is root-2 higher, i.e., 2^½ = 1.414 [mmag/min]. In other words, to convert precision to 1-minute equivalent exposures we may use the equation RMS1 = RMSi × g [minutes] ^½, where RMSi is the RMS for individual images with exposure time g. Note that the term in the previous step is 1 / RMS1² , so this term can be written 1 / ( RMSi² × g [minutes]).

Combining terms yields:  IR1 = DutyCycle  / ( RMSi² × g [minutes]) 

Referring back to Fig. 2, a LC for sharp-focus images, RMS2 = 0.95 and DutyCycle = 15 / (15 + 8 + 4) = 0.555. Therefore,

      IR1 (sharp-focus) = 0.555 / ( 0.95² × 2 )
                                  = 0.555 / 1.80
                                  = 0.308
which means that each minute provides only 41% of the information needed to achieve a precision of 1 mmag per minute. This is equivalent to stating "To achieve 1 mmag precision requires 2.4 minutes (1 / 0.41) of telescope time." Another equivalent statement is "Each minute produces a precision of 1.56 mmag (1 / 0.41^½ )."

The 15-second, sharp-focus images did not meet the desired goal of IR1 = 1.00, corresponding to 1 mmag precision each minute, but it does represent a level for IR1 that must be improved upon by defocusing in order for the defocusing strategy to have merit (for this target, hardware and observing condition).

As an aside, it is often stated that a purpose for defocusing is to reduce the effect of scintillation. Longer exposures reduce scintillation for individual images, to be sure, but whereas this improves RMSi it has only a small effect on RMS1, and hence information rate. The only benefit provided by the longer exposures is from an improved duty cycle. The very same argument applies to Poisson noise, which is also reduced for longer exposures, but again, this only improves RMSi and has only a small effect on RMS1, and hence information rate. The benefit is purely from a better duty cycle afforded by longer exposures. The thing to optimize is not RMSi, but IR1!

Defocus Observations

Three questions have to be answered when considering employing a defocusing strategy:
    1) When should defocuing be employed?
    2) How much should you defocus?
    3) How large a photometry aperture is optimum for processing the images? 

Faint targets shouldn't be defocused. For example, asteroid observing requires careful attention to focus in order to merely locate the asteroid for image processing. Bright targets can "require" defocusing in order to avoid extremely poor duty cycles. I'm going to address these questions in reverse order for the simple reason that the rest of the analyses will go faster. So first we'll determine a "rule" for setting the photometry aperture, then we'll figure out how much to defocus for a given star and finally we'll decide when to employ defocusing for "medium bright" stars.

Best Photometry Aperture Size

I'll use observations of another star field and another date to assess optimum photometry aperture radius (PAR) for images that are defocused enough to produce donut-shaped PSFs. One reeason for this is the desire to use a long stretch of data for adequately assessing whether a given PAR is better than ofther choices. On 2009.02.01 I observed HD 17156 continuously for 3 hours with a highly defocused setting. Focus was offset "out" a fixed amount and was updated using automatic temperature compensation in order to maintain the same defocus amount throughout the observing session. For these images the outer edge of the donut pattern had a radius of 12 pixels.

Figure 4. FOV of HD 17156 ("Obj") star field showing "donut" shapes and a photometry aperture radius much larger than the donut. FOV = 21 x 31 'arc, north up, east left. (2009.02.01)

There were 291 images, each exposed 30 seconds, which kept 8.17 V-magnitude HD 17156, the brightest star, below saturation (peak ~30,000 counts). Photometry measurements were made with PAR = 10, 12, 14, 16, 18 and 20 pixels. For each aperture radius an extensive procedure was used to select the best reference stars from among the 22 candidates. Outlier data were rejected in a way that maintained acceptance of 99% of the images. In effect, the final reference star selection was based on which set yielded the lowest noise and best fit to a simple model. Since this was an OOT observation the model consisted of a slope and air mass curvature (and offset). Following is the light curve for the 14-pixel radius fit.

 
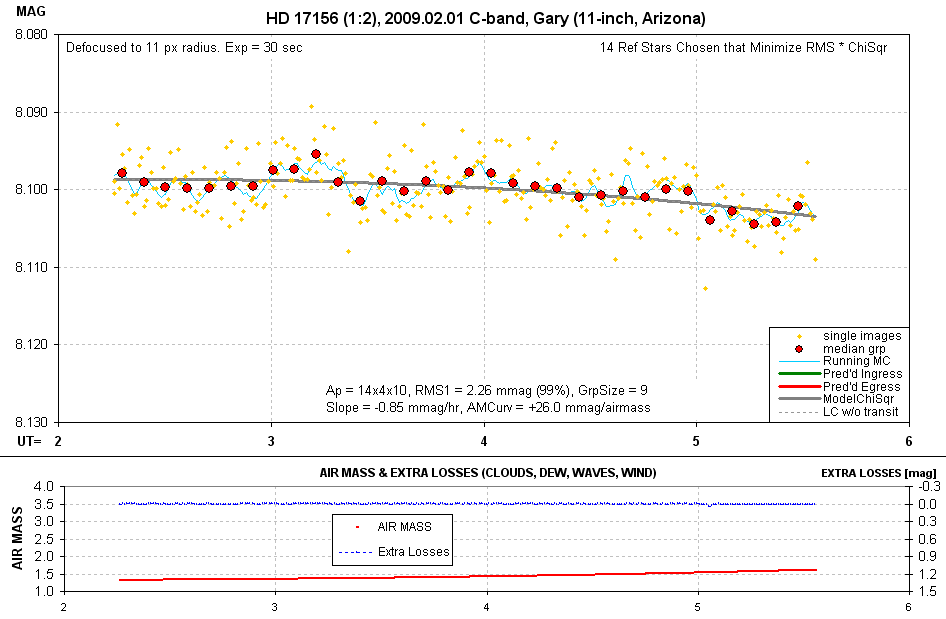
Figure 6. Light curve for the photometry aperture radius choice of 15 pixels after solving for a best fit (i.e., best choice of reference stars and model slope, air mass curvature and offset).

This LC has RMS1 = 2.26 mmag. Since DutyCycle = 0.71, IR1 = 0.14 (i.e., 0.71 / 2.26²). This is smaller than for the previous night, when IR1 = 0.32, due perhaps to greater air mass (hence worse seeing) and possible a greater level of scintillation.

The following plot shows "RMS with respect to the best fitting model" versus photometry aperture radius.

 
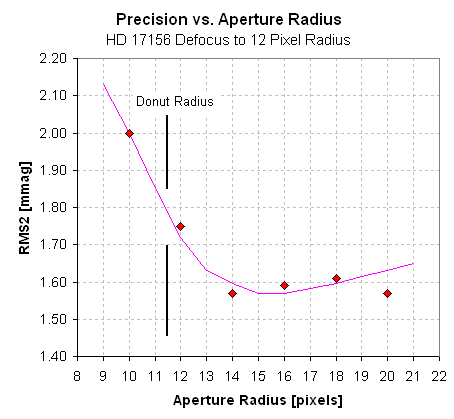
Figure 7. Dependence of RMS precision on photometry aperture radius (PAR) for highly-defocused, donut-shaped PSF .

Based on this one case study the following "rule" suggests itself:

        Optimum Photometry Aperture Radius = 1.30 ×"PSF Donut-Shaped Outer Edge Radius"

But wait, we have more ground-work before adopting a rule for estimating an optimum PAR. The above rule only applies to highly-defocused iamges; we need to address the matter of slightly-defocused images. Hopefully we can discover a universal principle that related optimum PAR to FFR for all images, regardless of focus.

Estimating Optimum PAR

So far I've shown a way to estimate optimum PAR for sharply-focused images and highly-defocused images, summarized here:

    Optimum PAR = FWHM ×4 for sharply-focused images, and

    Optimum PAR = 1.3 × Radius to Outer Edge of Donut-Shaped PSF for highly-defocused images.

What about slightly-defocused images? It sure would be handy to have a "rule" that applies to all three focus regimes.

Consider a bright star in sharp focus, and let's ask the question "How does flux vary with PAR?" Here's the answer for one of my sharply-focused images:

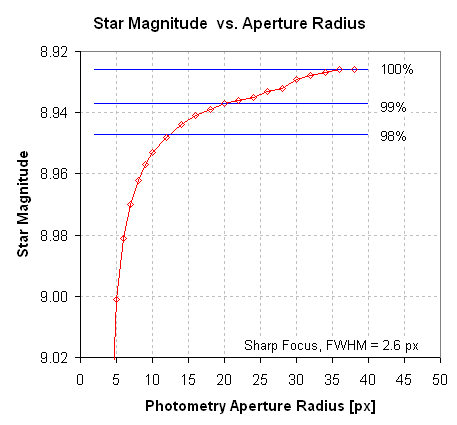
Figure 8. Star magnitude versus PAR. 98% of the star's flux is contained within a radius of ~12 pixels.

It's surprising that flux within an aperture circle just keeps increasing well beyond where visual inspection thinks star flux exists. The next image has circles enclosing 98%, 99% and 100% of the star's total flux.

Figure 8. Bright star used to determine FFR. The inner circle encloses 98% of the total star flux (PAR=12 px), the middle circle encloses 99% (PAR=20 px), and the outer circle includes ~100% (PAR=36 px). FWHM = 2.6 pixels, or 3.2 "arc. (I pixel edited to remove an interfering star below the target star.)

Referring back to Fig. 3, where it is shown that the optimum PAR ~ 4.5 × FWHM, we surmise that if a flux percentage is to be used to estimate optimum PAR we might use the 98% criterion (referring to Fig. 7).

The suggestion, therefore, is that instead of estimating optimum PAR from FWHM we instead determine what PAR produces 98% of the star's total flux. I wonder if this criterion would also work for highly-defocused stars?

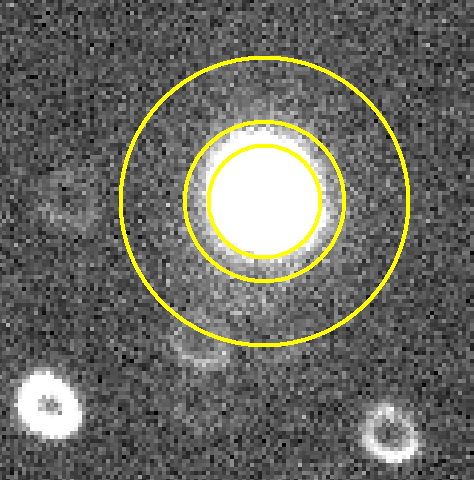
Figure 9. Highly-defocused image with circles placed to correspond to 98%, 99% and ~100% of the star's flux. The PAR values are 14, 20 and 36 pixels. 

Note that the 98% flux circle is achieved for PAR = 14 pixels. Referring back to Fig. 7 this is the PAR we want for optimum precision! So,

        "Optimum PAR can be established by determining what PAR value encloses 98% of the star's flux for both sharply-focused and highly-defocused images."

This is convenient! Note that optimum PAR for sharply-focused and highly-defocused stars is about the same: 12 and 14 pixels. It is tempting to assume that partially-defocused images will have an optimum PAR of ~13 pixels. This is a reasonable speculation because the PSFs for the three focus regimes will increase in size uniformly with increasing defocus. I hereby adopt the above "rule" for determining optimum PAR.

Definition of Defocus Amount: Defocus75

Based on the success of the previous exercise for determining optimum PAR from percentage flux measurements, I hereby propose to define a parameter based on the 75% of total flux circle for use in quantifying how much defocus is present in an image. Let's give this paramater a name, PAR75. Consider the following three images:

Figure 10. Sharply-focused image, with PAR75 = 2.7 px (inner circle is PAR = 3 px). FWHM 2.4 pixels (2.9"arc). FOV = 2.5 x 1.6 'arc.

Figure 11. Slightly-defocused image, with PAR75 = 4.3 px (inner circle is PAR = 4 px).

Figure 12. Highly-defocused image, with PAR75 = 6.5 px (inner circle is PAR = 7 px).

For this observing session (2009.01.31), and for my hardware (image scale 1.21 "arc, etc), the sharpest possible image has PAR75 ~ 2.7 px. If we subtract this value from any other image's PAR75 we will have a measure of the defocus amount. For the above three images, we have:

    dFOC = PAT75 - 2.7 px (for this observing session, 2009.01.31)

    dFOC = 3.8 px for the highly-defocused image
    dFOC = 1.6 px for the slightly-defocused image
    dFOC = 0.0 px for the sharply-focused image
 
Light Curve Precision versus Defocus Value

We're now ready to analyze images with different amounts of defocusing and compare precision with the amount of defocus.

On 2009.01.31 I observed the 9th magnitude star described in the above section, "Review of Usual Strategy for Sharply-Focused Exoplanet Light Curves." For each of the 10 defocus settings I observed for 10 minutes, using 15-second expsoure times. About 30 images are available for analysis for each defocus setting. We have already seen the LC precision for sharply-focused images (Fig. 2). The precision is ~0.95 mmag per 2-minute equivalent exposure. Our goal is to determine how much better we can do by defocusing. Let's begin with a highly-defocused set of images from the 2009.01.31 observing session. In the following table "Focus Set'g" is listed in terms of whether the focuser is in "i" or out "o" with respect to a sharp focus setting.

  Focus   dFOC   RMS1
  Set'g    px    mmag    

        i55   2.9    1.80  
    i45   2.4    1.86
    i30   1.7    1.69
    DF0   0.0    1.32
    o20   1.2    0.96
    o30   1.8    1.02
    o45   2.6    1.26
    o55  
    o65  
    o75  

There's a smooth pattern of RMS1 versus focus setting that favors a slight defocus in the "out" direction. A slight defocus in the "in" direction has greater RMS1. 

[more coming...]

Why? 

I used to think that the only reason for defocusing was to improve duty cycle. But compare the "sharply focused image set with large aperture" with "defocused image set with large aperture" (same apertures), and the RMS per 2-minute equivalent image, unadjusted for duty cycle, is better for the defocused image than for the sharp image. The two precisions are 3.09 mmag per image and 2.02 mmag per image. Since duty cycle has nothing to do with these two precision calculations there's something going on that has to do with the spreading out of where photo-electrons are produced.

Could it be that when most of the star's photo-electrons originate from only a few pixels that the readout noise per pixel, or the thermal noise per pixel, has a greater percentage effect on the total flux than when many pixels are involved? When most of the photo-electrons come from just a few pixels could small errors in the flat field contribute a greater error in the total flux than when these flat field errors are averaged-out over more pixels? Could someone help me understnad this?

Conclusion

WebMaster: B. Gary.  Nothing on this web page is copyrighted. This site opened:  2009.01.31.  Last Update:  2009.02.09